Электромагнитная индукция
· Закон Фарадея
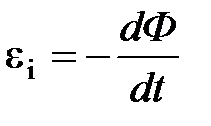 ,
,
где 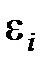 – ЭДС индукции.
– ЭДС индукции.
· Э.д.с. индукции, возникающая в рамке площадью 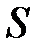 при вращении рамки с угловой скоростью
при вращении рамки с угловой скоростью 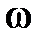 в однородном магнитном поле с индукцией
в однородном магнитном поле с индукцией 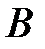 ,
,
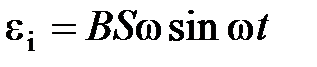 ,
,
где 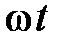 – мгновенное значение угла между вектором
– мгновенное значение угла между вектором 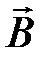 и вектором
и вектором 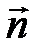 нормали
нормали 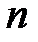 к плоскости рамки.
к плоскости рамки.
· Магнитный поток, создаваемый током 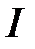 в контуре с индуктивностью
в контуре с индуктивностью 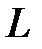
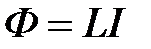 .
.
· ЭДС самоиндукции
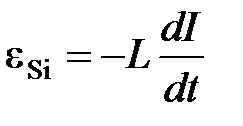 ,
,
где 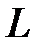 – индуктивность контура.
– индуктивность контура.
· Индуктивность соленоида (тороида):
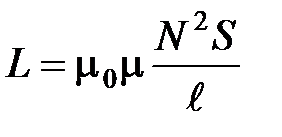 ,
,
где 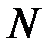 – число витков соленоида;
– число витков соленоида; 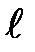 – его длина.
– его длина.
· Токи при размыкании и примыкании цепи
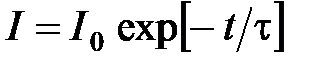 ;
; 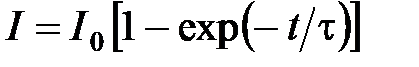 ,
,
где 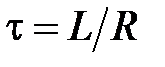 – время релаксации (
– время релаксации ( 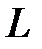 – индуктивность;
– индуктивность; 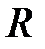 – сопротивление).
– сопротивление).
· ЭДС взаимной индукции (ЭДС, индуцируемая изменением силы тока в соседнем контуре):
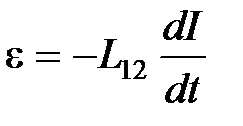 ,
,
где 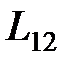 – взаимная индуктивность контуров.
– взаимная индуктивность контуров.
· Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью 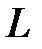 , по которому течет ток
, по которому течет ток 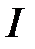 ,
,
W = LI2/2.
· Объемная плотность энергии однородного магнитного поля длинного соленоида
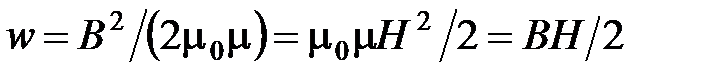 .
.
Магнитные свойства вещества
· Связь орбитального магнитного 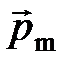 и орбитального механического
и орбитального механического 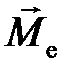 моментов электрона
моментов электрона
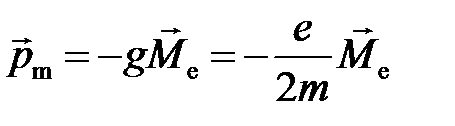 ,
,
где 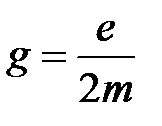 – гиромагнитное отношение орбитальных моментов.
– гиромагнитное отношение орбитальных моментов.
· Намагниченность
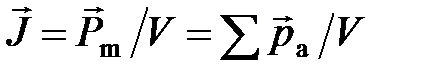 ,
,
где 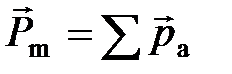 – магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.
– магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.
· Связь между намагниченностью и напряженностью магнитного поля
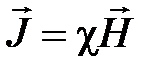 , где
, где 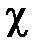 – магнитная восприимчивость вещества.
– магнитная восприимчивость вещества.
· Связь между векторами 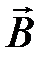 ,
, 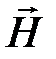 ,
, 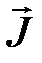
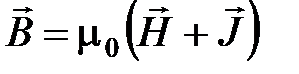 , где
, где 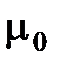 – магнитная постоянная.
– магнитная постоянная.
· Связь между магнитной проницаемостью и магнитной восприимчивостью вещества
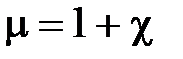
· Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора 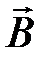 )
)
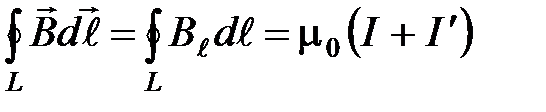 ,
,
где 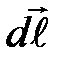 – вектор элементарной длины контура, направленный вдоль обхода контура;
– вектор элементарной длины контура, направленный вдоль обхода контура; 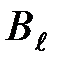 – составляющая вектора
– составляющая вектора 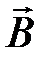 в направлении касательного контура
в направлении касательного контура 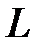 произвольной формы;
произвольной формы; 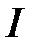 и
и 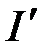 соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых заданным контуром.
соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых заданным контуром.
· Теорема о циркуляции вектора напряженности магнитного поля
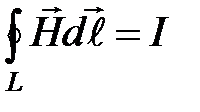 ,
,
где 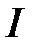 – алгебраическая сумма токов проводимости, охватываемых контуром
– алгебраическая сумма токов проводимости, охватываемых контуром 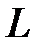 .
.
Основы теории Максвелла для электромагнитного поля
· Плотность тока смещения
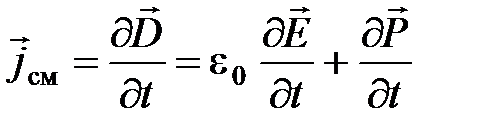 ,
,
где 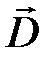 электрическое смещение;
электрическое смещение; 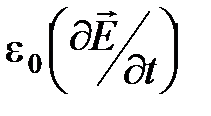 – плотность тока смещения в вакууме;
– плотность тока смещения в вакууме; 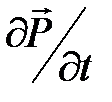 – плотность тока поляризации.
– плотность тока поляризации.
· Полная система уравнений Максвелла:
в интегральной форме
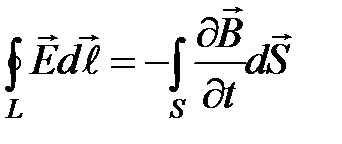 ;
; 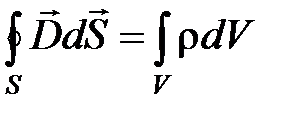 ;
;
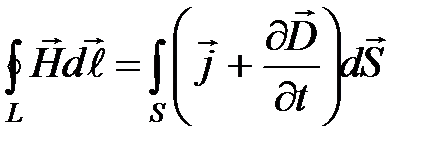 ;
; 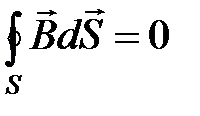 ,
,
в дифференциальной форме
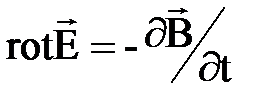 ;
; 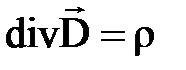 ;
;
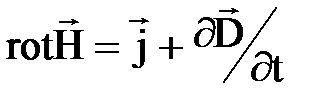 ;
; 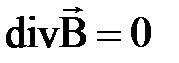 ,
,
где 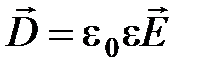 ;
; 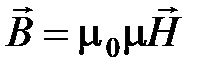 ;
; 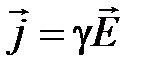 (
( 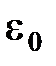 и
и 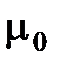 – соответственно электрическая и магнитная постоянные;
– соответственно электрическая и магнитная постоянные; 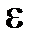 и
и 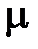 – диэлектрическая и магнитная проницаемости;
– диэлектрическая и магнитная проницаемости; 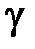 – удельная проводимость вещества).
– удельная проводимость вещества).
Физика колебаний и волн
