Фазовые равновесия и фазовые переходы
План
Фазы вещества. Равновесие фаз. Фазовая диаграмма (диаграмма состояния). Тройная точка. Уравнение Клайперона – Клаузиуса.
Фазой называется макроскопическая физически однородная часть вещества, отделённая от остальных частей системы поверхностью раздела. Фазовое равновесие – одновременное существование фаз в многофазной системе (без изменения одной фазы за счет другой).
Разные фазы одного и того же вещества могут находиться в равновесии, соприкасаясь друг с другом. Такое равновесие наблюдается лишь в ограниченном интервале температур, причём каждому значению температуры 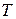 соответствует своё значение давления
соответствует своё значение давления 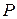 , при котором возможно равновесие. Совокупность состояний равновесия 2-х фаз изображается на диаграмме
, при котором возможно равновесие. Совокупность состояний равновесия 2-х фаз изображается на диаграмме 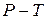 линией
линией 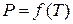 . Три фазы одного и того же вещества (твёрдая, жидкая и газообразная или жидкая и две твёрдых или три твёрдых) могут находиться в равновесии только при единственных значениях температуры и давления, которые на диаграмме
. Три фазы одного и того же вещества (твёрдая, жидкая и газообразная или жидкая и две твёрдых или три твёрдых) могут находиться в равновесии только при единственных значениях температуры и давления, которые на диаграмме 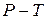 соответствует точка, называемая тройной.
соответствует точка, называемая тройной.
В термодинамике доказывается, что равновесие более чем 3-х фаз одного и того же веществаневозможно (и это подтверждено экспериментально).
Диаграмма состояния. (рис. 12.1)
 | 1-2-3 переход кристалл  жидкость жидкость  газ 4-5 кристалл газ 4-5 кристалл 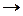 газ 6-7 переход из жидкости в газ без расслоения на фазы. газ 6-7 переход из жидкости в газ без расслоения на фазы. |
| Рис. 12.1 |
Определение. Сублимация (возгонка) – непосредственный (без плавления) переход из кристаллического состояния в газообразное.
Из диаграммы (рис. 12.1) следует, что жидкая фаза может находиться в равновесии при давлениях не меньше, чем давление в тройной точке 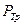 . Например, в случае углекислоты (
. Например, в случае углекислоты ( 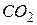 )
) 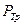 =5,11 атм, поэтому при атмосферном давлении (1 атм.) углекислота может существовать только в твёрдом и газообразном состояниях. Твёрдая углекислота (называемая сухим льдом) на воздухе сублимирует, а не тает (переход 4-5). Для большинства же обычных веществ
=5,11 атм, поэтому при атмосферном давлении (1 атм.) углекислота может существовать только в твёрдом и газообразном состояниях. Твёрдая углекислота (называемая сухим льдом) на воздухе сублимирует, а не тает (переход 4-5). Для большинства же обычных веществ 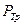 значительно меньше атмосферного давления (например, для
значительно меньше атмосферного давления (например, для 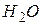
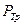 =4,58 мм. рт. ст.), поэтому переход из кристаллического состояния в газообразное осуществляется через жидкую фазу.
=4,58 мм. рт. ст.), поэтому переход из кристаллического состояния в газообразное осуществляется через жидкую фазу.
Кривая испарения заканчивается в критической точке К. Поэтому возможен процесс в обход критической точки К. в этом случае переход из жидкого состояния в газообразное совершается непрерывно (процесс 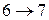 ) без расслаивания на две фазы. При температурах выше критической вещество не может быть сжижено никаким сжатием.
) без расслаивания на две фазы. При температурах выше критической вещество не может быть сжижено никаким сжатием.
Фазовые переходы с поглощением или выделением скрытой теплоты перехода называются фазовыми переходами первого рода. Например, в процессах плавления или кристаллизации. Фазовые переходы, не связанные со скрытой теплотой перехода, называются фазовыми переходами второго рода. Например, переход парамагнетик – ферромагнетик.
Уравнение Клапейрона – Клаузиуса
(без вывода).
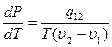 |
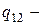 теплота фазового перехода,
теплота фазового перехода, 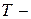 температура,
температура, 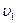 и
и 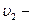 объёмы обеих фаз. (
объёмы обеих фаз. ( 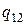 и
и 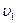 ,
, 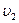 относятся к одному и тому же количеству вещества, например, к 1 молю или 1 кг, т.е. является удеальными).
относятся к одному и тому же количеству вещества, например, к 1 молю или 1 кг, т.е. является удеальными).
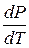 определяет наклон фазовой кривой фазового равновесия Р(Т). Уравнение Клапейрона – Клаузиуса даёт изменение температуры фазового перехода при изменении давления.
определяет наклон фазовой кривой фазового равновесия Р(Т). Уравнение Клапейрона – Клаузиуса даёт изменение температуры фазового перехода при изменении давления.
Пример. Для воды (льда) теплота плавления 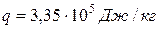 . Разница удельных объёмов льда и воды при 0
. Разница удельных объёмов льда и воды при 0 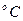
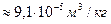 (легко найти из соответствующих плотностей).
(легко найти из соответствующих плотностей).
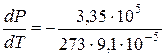
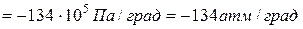 . То есть, с увеличением давления на одну атмосферу точка плавления льда понижается примерно на 0,0075 град.
. То есть, с увеличением давления на одну атмосферу точка плавления льда понижается примерно на 0,0075 град.
Опыт. Если на брусок льда, лежащий своими концами на неподвижных опорах, накинуть проволочную петлю, и к ней подвесить тяжёлый груз, то лёд под проволокой плавится. Вода выдавливается из-под проволоки и замерзает над ней. Проволока постепенно проходит через брусок, однако брусок остаётся неразрезанным.
Вопросы для самоконтроля.
1. Что называется фазой?
2. Нарисуйте фазовую диаграмму состояния в Р-Т координатах. Ука-
жите на ней тройную точку. Каков ее смысл?
3. Приведите примеры фазовых переходов и укажите их на диаграмме
состояния.
4. Запишите уравнение Клапейрона – Клаузиуса. Какие величины оно
связывает? Приведите пример использования этого уравнения.
Лекция №7 (13)
