Когда длинный путь проходится быстрее, чем короткий?
Но неужели ломаный путь может быстрее привести к цели, чем прямой? Да, в тех случаях, когда скорость движения в различных частях пути различна. Вспомните, что приходится делать жителям деревни, расположенной между двумя железнодорожными станциями в соседстве с одной из них. Чтобы попасть скорее на дальнюю станцию, они едут на лошади сначала в обратном направлении, к ближайшей станции, там садятся в поезд и едут на место назначения. Им короче было бы, разумеется, прямо ехать туда на лошади, но они предпочитают более длинный путь на лошади и в вагоне, потому что он приводит к цели скорее.

Рис. 110. Задача о кавалеристе. Найти скорейший путь из A в С.
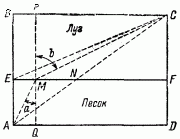
Рис. 111. Решение задачи о кавалеристе. Скорейший путь АМС.
Уделим минуту внимания еще одному примеру. Кавалерист должен прибыть с донесением из точки А к палатке командира в точке C (рис. 110). Его отделяют от палатки полоса глубокого песка и полоса луга, разграниченные между собой прямой линией EF. По песчаной почве лошадь движется вдвое медленнее, чем по лугу. Какой же путь должен выбрать кавалерист, чтобы достигнуть палатки в кратчайшее время?
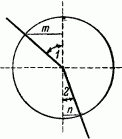
Рис. 112. Что такое синус? Отношение m к радиусу есть синус угла 1, отношение n к радиусу – синус угла 2.
На первый взгляд кажется, что самый скорый путь – прямая линия, проведенная от A до С. Но это совершенно ошибочно, и я не думаю, чтобы нашелся кавалерист, который выбрал бы такой путь. Медленное движение по песку наведет его на правильную мысль сократить эту медленную часть пути, прорезав песчаную полосу по менее косой линии; конечно, тем самым удлинится вторая часть пути – по лугу; но так как по лугу можно двигаться вдвое быстрее, то удлинение пути не перевесит полученной выгоды, и в общем итоге путь будет проделан в меньший промежуток времени. Другими словами, путь кавалериста должен преломиться на границе обоих родов почвы и притом так, чтобы путь по лугу составлял с перпендикуляром к границе больший угол, чем путь по песчаной почве.
Кто знаком с геометрией, именно с теоремой Пифагора, тот может проверить, что прямой путь AC действительно не является путем скорейшим и что при тех размерах для ширины полос и расстояний, которые мы здесь имеем в виду, можно скорее достичь цели, если направиться, например, по ломаной АЕС (рис. 111).
На рис. 110 указано, что ширина песчаной полосы 2 км, луговой – 3 км, а расстояние ВС – 7 км. Тогда вся длина AC (рис. 111) равна, по теореме Пифагора, корень(52 + 72) = корень(74) = 8,60 км. Часть AN – путь по песку – этого отрезка составляет, как легко сообразить, 2/5 этой величины, т. е. 3,44 км. Так как по песку движение происходит вдвое медленнее, чем по лугу, то 3,44 км песчаного пути равнозначны, в смысле требуемого времени, 6,88 км по лугу. И, следовательно, весь смешанный путь по прямой АС, равный 8,60 км, соответствует 12,04 км пути по лугу.
Сделаем такое же «приведение к лугу» и для ломаного пути АЕС. Часть АЕ = 2 км и соответствует 4 км пути по лугу. Часть ЕС = корень(32 + 72) = корень(58) = 7,61 км. Итого весь ломаный путь AEC отвечает 4 + 7,61 = 11,61 км.
Итак, «короткий» прямой путь соответствует 12,04 км движения по лугу, а «длинный» ломаный – всего только 11,61 км по той же почве. «Длинный» путь, как видите, дает выгоду в 12,04–11,61 = 0,43, почти в полкилометра!
Но мы не указали еще самого быстрого пути. Быстрейший путь, как учит теория, будет тот, при котором (нам придется здесь обратиться к услугам тригонометрии) синус угла b относится к синусу угла A, как скорость на лугу относится к скорости на песке, т. е. как 2:1. Другими словами, нужно выбрать направление так, чтобы sin b был вдвое больше sin а. Для этого нужно перешагнуть границу между полосами в такой точке m, которая находится в одном километре от Е. Действительно, тогда sin b = 6/(корень(32 + 62)), sin a = 1/(корень(1 + 22)), отношение sin b/sin a = (6/корень(45))/(1/ (3*корень(5))) = (6/(3*корень(5)))/(1/корень(5)) = 2, т. е. как раз отношению скоростей.
А какова будет в таком случае «приведенная к лугу» длина пути? Вычислим: AM = корень(22 + 12), что отвечает 4,47 км пути по лугу. МС = корень(45) = 6,71 км. Длина всего пути 4,47 + 6,71 = 11,18, т. е. на 860 км короче прямолинейного пути, который, как мы уже знаем, соответствует 12,04 км.
Вы видите, какие выгоды доставляет при данных условиях изламывание пути. Световой луч как раз и избирает такой скорейший путь, потому что закон преломления света строго удовлетворяет требованию математического решения задачи: синус угла преломления относится к синусу угла падения, как скорость света в новой среде к скорости его в покидаемой среде; с другой стороны, это отношение равно показателю преломления света в указанных средах.
Объединяя в одно правило особенности и отражения и преломления, мы можем сказать, что световой луч во всех случаях следует по быстрейшему пути, т. е. подчиняется правилу, которое физики называют «принципом скорейшего прихода» (принцип Ферма).
Если среда неоднородна и ее преломляющая способность меняется постепенно, как, например, в нашей атмосфере, то и в таком случае вполне осуществляется быстрейший приход. Этим объясняется то небольшое искривление лучей небесных светил в атмосфере, которое на языке астрономов называется «атмосферной рефракцией». В атмосфере, постепенно уплотняющейся книзу, луч света изгибается так, что вогнутость его обращена к Земле. Тогда луч остается дольше в высоких слоях, которые слабее замедляют его путь, и проводит меньше времени в «медленных» низких слоях, в итоге он приходит к цели быстрее, чем по пути строго прямолинейному.
Принцип быстрейшего прихода (принцип Ферма) справедлив не для одних лишь световых явлений: ему в полной мере подчиняется также распространение звука и всех вообще волнообразных движений, какова бы ни была природа этих волн.
Читатель, без сомнения, желал бы узнать, чем объясняется это свойство волнообразных движений. Приведу поэтому относящиеся сюда соображения, высказанные выдающимся современным физиком Шредингером [В докладе, прочитанном в Стокгольме при получении Нобелевской премии (в 1933 г.)]. Он исходит из знакомого уже нам примера марширующих солдат и имеет в виду случай движения светового луча в среде постепенно изменяющейся плотности.
«Пусть, – пишет он, – для того, чтобы сохранить строгую правильность фронта, солдаты соединены длинным шестом, который каждый из них крепко удерживает в руках. Команда гласит: всем бежать возможно быстрее! Если характер почвы медленно меняется от точки к точке, то сначала, скажем, правое, а позднее левое крыло фронта будет подвигаться быстрее – и поворот фронта осуществится сам собой. Мы заметим при этом, что пройденный путь – не прямолинейный, а искривленный. То, что путь этот строго совпадает с кратчайшим в смысле времени прибытия в данный пункт при заданных свойствах почвы, – довольно понятно, так как ведь каждый солдат старался подвигаться как можно быстрее».
Новые Робинзоны
Без сомнения, вы знаете, как герои романа Жюля Верна «Таинственный остров», заброшенные на необитаемую землю, добыли огонь без спичек и огнива. Робинзону явилась на помощь молния, зажегшая дерево, новым же Робинзонам Жюля Верна помогла не случайность, а находчивость сведущего инженера и твердое знание им законов физики. Помните, как удивился наивный моряк Пенкроф, когда, возвратившись с охоты, нашел инженера и журналиста перед пылающим костром.
«– Но кто же зажег огонь? – спросил моряк.
– Солнце, – ответил Спилетт.
Журналист не шутил. Действительно, Солнце доставило огонь, которым так восторгался моряк. Он не верил своим глазам и был до того изумлен, что даже не мог расспрашивать инженера.
– Значит, у вас было зажигательное стекло? – спросил инженера Герберт.
– Нет, но я его изготовил.
И он его показал. Это были просто два стекла, снятые инженером со своих часов и часов Спилетта. Он соединил их края глиной, предварительно наполнив водой, и таким образом получилась настоящая зажигательная чечевица, с помощью которой, сосредоточив солнечные лучи на сухом мхе, инженер добыл огонь».
Читатель пожелает, я думаю, узнать, зачем нужно заполнять водой пространство между часовыми стеклами: разве наполненная воздухом двояковыпуклая чечевица не сосредоточивает лучей?
Именно нет. Часовое стекло ограничено двумя параллельными (концентрическими) поверхностями – наружной и внутренней; а известно из физики, что, проходя через среду, ограниченную такими поверхностями, лучи почти не изменяют своего направления. Проходя затем через второе такое же стекло, они и здесь не отклоняются, а следовательно, не собираются в фокусе. Чтобы сосредоточить лучи в одной точке, необходимо заполнить пространство между стеклами каким‑нибудь прозрачным веществом, которое преломляло бы лучи сильнее, нежели воздух. Так и поступил инженер в романе Жюля Верна.
Обыкновенный графин с водой, если имеет шарообразную форму, также может служить зажигательной чечевицей. Это знали уже древние, которые заметили и то, что сама вода при этом остается холодной. Случалось даже, что стоящий на открытом окне графин с водой зажигал занавески, скатерть, обугливал стол. Те огромные шаровые бутылки с окрашенной водой, которые, по старинному обычаю, украшали раньше витрины аптек, могли быть иногда причиной настоящих катастроф, вызывая возгорание легко воспламеняющихся веществ, расположенных поблизости.
Небольшой круглой колбой, наполненной водой, можно даже при небольших размерах колбы довести до кипения воду, налитую на часовое стеклышко: для этого достаточна колба сантиметров в 12 диаметром. При 15 см в фокусе [Фокус помещается при этом весьма близко к колбе] получается температура 120°. Зажечь папироску с помощью колбы с водой так же легко, как и стеклянной чечевицей, о которой еще Ломоносов в своем стихотворении «О пользе стекла» писал:
Мы пламень солнечный стеклом здесь получаем
И Прометею тем безбедно подражаем.
Ругаясь подлости нескладных оных врак,
Небесным без греха огнем курим табак.
Следует заметить, однако, что зажигательное действие водяных линз значительно слабее, чем стеклянных. Это связано, во‑первых, с тем, что преломление света в воде гораздо меньше, чем в стекле, во‑вторых, вода в сильной степени поглощает инфракрасные лучи, которые играют большую роль в нагревании тел.
Любопытно, что зажигательное действие стеклянных чечевиц известно было еще древним грекам, более чем за тысячелетие раньше изобретения очков и зрительных труб. О нем упоминает Аристофан в знаменитой комедии «Облака». Сократ предлагает Стрептиаду задачу:
«Если бы кто писал обязательство на тебя в пяти талантах, как бы ты уничтожил оное?
Стрептиад. Нашел я, как истребить обязательство, да такой способ, что ты и сам признаешь его прехитрым! Видал ты, конечно, в аптеках камень прекрасный, прозрачный, которым зажигают?
Сократ. Зажигательное стекло?
Стрептиад. Точно так.
Сократ. Что же далее?
Стрептиад. Пока нотариус пишет, я, став позади его, направлю лучи Солнца на обязательство, да слова‑то все и растоплю…»
Напомню для пояснения, что греки времен Аристофана писали на навощенных дощечках, которые от тепла легко растапливались.
