I. ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ Основные формулы

Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси х

x = f(t),

где /(/) — некоторая функция времени. Проекция средней скорости на ось х

<°*>=-дТ-

Средняя путевая скорость

<^У>=^Г'

где As — путь, пройденный точкой за интервал време­ни А/. Путь As в отличие от разности координат Ах~ = Х2 — Х\ не может убывать и принимать отрицательные значения, т.е. As^O.

Проекция мгновенной скорости на ось х

Ах

Проекция среднего ускорения на ось х

Проекция мгновенного ускорения на ось х

а_х= —- . At

Кинематическое уравнение движения материальной точки по окружности

Ф = Я0> r — R = const.

Модуль угловой скорости

At ■ Модуль углового ускорения

da> 8 = — .

At

Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

v = (aR, a_x = sR, a_n = со²/?,

где v — модуль линейной скорости; а_т и а„ — модули тангенциального и нормального ускорений; со — модуль угловой скорости; е — модуль углового ускорения; R — радиус окружности.

Модуль полного ускорения

а =д/ an-f-a² , или а = Ry е²-\-а⁴.

Угол между полным а и нормальным а„ ускорениями

а= arc cos (a„/a).

Кинематическое уравнение гармонических колебаний материальной точки

х = А соэ(со/ + ф),

где х — смещение; Л — амплитуда колебаний; со — уг­ловая или циклическая частота; ф — начальная фаза. Скорость и ускорение материальной точки, совершаю­щей гармонические колебания:

v = —Лео sin (со/ + ф)". ^а = —Лео² соз(со/ + ф).

Сложение гармонических колебаний одного направ­ления и одинаковой частоты:

а) амплитуда результирующего колебания

Л =Ул²+Л|-_г-2Л1Л₂соз(ф2 —фО ;

б) начальная фаза результирующего колебания

Ф = arc tg — -Н—; *^L ■

^T ° A\ coscpi+j42 cosq>2

Траектория точки, участвующей в двух взаимно пер­пендикулярных колебаниях,

х = Л1Созсо^; у = Л₂со5(со/+ф)-

а) у = -—-х, если разность фаз ф=0;

б) у =-------- -р-х, если разность фаз ф=±я;

в) •4т + -7Г⁼⁼1. ^если разность фаз ф=±-у.
14

Уравнение плоской бегущей волны

у = A cos со ( f ^-j ,

где у — смещение любой из точек среды с координатой х в момент t; v — скорость распространения колебаний в среде.

Связь разности фаз Дф колебаний с расстоянием Ах между точками среды, отсчитанным в направлении рас­пространения колебаний;

Лф = -£-Дл:,

где % — длина волны.

Импульс материальной точки массой т, движущейся со скоростью v,

р = тх.

Второй закон Ньютона

dp = Fd/,

где F — результирующая сила, действующая на ма­териальную точку.

Силы, рассматриваемые в механике:

а) сила упругости

F = — kx,

где k — коэффициент упругости (в случае пружины — жесткость); х — абсолютная деформация;

б) сила тяжести

Р= mg;

в) сила гравитационного взаимодействия

r = <J—р—,

где G — гравитационная постоянная; mi и т₂ — массы взаимодействующих тел; г — расстояние между телами (тела рассматриваются как материальные точки). В слу­чае гравитационного взаимодействия силу можно выра­зить также через напряженность G гравитационного поля:

F = mG;

г) сила трения (скольжения) F = fN,

где / — коэффициент трения; N — сила нормального дав­ления.

Закон сохранения импульса

N

2 Р< = const,

1=1

или для двух тел (г=2)

miVi-f-m₂v₂=miUi -j- m₂u₂,

где Vi и V2 — скорости тел в момент времени, принятый за начальный; Ui и и₂ — скорости тех же тел в момент времени, принятый за конечный.

Кинетическая энергия тела, движущегося поступа­тельно,

Т = mv²/2, или Т = р²/{2т).

Потенциальная энергия:

а) упругодеформированной пружины

T\=^l/₂kx²,

где k — жесткость пружины; х — абсолютная дефор­мация;

б) гравитационного взаимодействия

П = — Gmi/n₂/r,

где G — гравитационная постоянная; т\ и т₂ — массы взаимодействующих тел; г — расстояние между ними (тела рассматриваются как материальные точки);

в) тела, находящегося в однородном поле силы
тяжести,

П = mgh,

где g — ускорение свободного падения; h — высота тела над уровяем, принятым за нулевой (формула справедли­ва при условии й<Я, где # —радиус Земли). Закон сохранения механической энергии

£== Г + П = const.

Работа А, совершаемая результирующей силой, опре­деляется как мера изменения кинетической энергии ма­териальной точки:

Л = ЛГ= Т₂ — Ti.

Основное уравнение динамики вращательного движе­ния относительно неподвижной оси z

М_г = /_ге,

где М_г — результирующий момент внешних сил относи­тельно оси z, действующих на тело; е — угловое ускоре­ние; /_г — момент инерции относительно оси вращения. Моменты инерции некоторых тел массой пг относи­тельно оси z, проходящей через центр масс:

а) стержня длиной / относительно оси, перпендику­
лярной стержню,

/_г=7.₂т/²;

б) обруча (тонкостенного цилиндра) относительно
оси, перпендикулярной плоскости обруча (совпадающей
с осью цилиндра),

Jz=mR\

где R — радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендику­
лярной плоскости диска,

]_г = ^l/₂mR².

Проекция на ось z момента импульса тела, вращаю­щегося относительно неподвижной оси z,

L_z = /_гсо,

где со — угловая скорость тела.

Закон сохранения момента импульса систем тел, вра­щающихся вокруг неподвижной оси г,

/_гсо = const,

где /₂ — момент инерции системы тел относительно оси z; со — угловая скорость вращения тел системы во­круг оси z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,

Т = ' /₂/_гсо², или Т = L²/(2J_Z).

Примеры решения задач

Пример 1.Уравнение движения материальной точки вдоль оси имеет вид x = A-\-Bt + Ct³, где А = 2 м, В = = 1 м/с, С=—0,5 м/с³. Найти координату х, скорость v_x и ускорение а_х точки в момент времени t = 2c.

Решение. Координату х найдем, подставив в урав­нение движения числовые значения коэффициентов А, В и С и времени t:

х = (2+1-2-0,5-2³) м = 0.

Мгновенная скорость относительно оси х есть первая производная от координаты по времени:

ах И

Vx =

В + ЗСР.

Ускорение точки найдем, взяв первую производную от скорости по времени:

а_х = —— = bCt.

В момент времени / = 2с

d, = (1-3-0,5-2²) м/с== -5 м/с; а^ = 6(-0,5)-2м/с² = -6 м/с².

Пример2. Тело вращается вокруг неподвижной оси по закону ср = A + Bt-\-Ct², где Л =10 рад, В = 20 рад/с, С=—2 рад/с². Найти полное ускорение точки, находя­щейся на расстоянии г=0,1 м от оси вращения, для момента времени г=4 с.

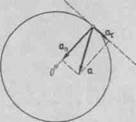
Решение. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометричес кая сумма тангенциального ускорения а_т, направленного по касательной к траектории, и нормального ускоре­ния а_л, направленного к центру кривизны траектории

(рис. 1):

а = а_т + а„.

Так как векторы а_т и а„ взаимно перпендикулярны то модуль ускорения

(1)

а = лГс& + а²_п .

и

Модули тангенциального нормального ускорения точк вращающегося тела выражаются формулами

ат = ег,

а_п = ш г,

Рис. 1

где <о — модуль угловой скорост тела; е — модуль его угловог ускорения.

Подставляя выражения а_т и а„ в формулу (1), на­ходим

_a=-VeV + uV = ,Ve² + tD⁴. (2)

Угловую скорость to найдем, взяв первую производ­ную угла поворота по времени:

ш = ^2.= В + 2Ct.

В момент времени ^=4с модуль угловой скорости

(о = [20 + 2(— 2)4] рад/с =4 рад/с.

Угловое ускорение найдем, взяв первую производную от угловой скорсти по времени:

е= doj/di= 2C= —4 рад/с².

Подставляя значения ы, е и г в формулу (2), полу­чаем

а = 0,г\/~(--4)² + 4⁴ м/с* =1,66 м/с².

Пример3. Ящик массой mi=20 кг соскальзывает по идеально гладкому лотку длиной /=2м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой т₂==80 кг может свободно (без трения) переме­щаться по рельсам в горизонтальном направлении. Опре­делить скорость и тележки с ящиком, если лоток накло­нен под углом а=30° к рельсам.

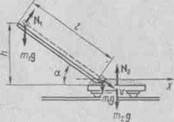Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел. Но эта система не замкнута, так как на нее действуют внеш­ние силы: силы тяжести m\g и m₂g и сила реакции 1М₂ (рис. 2). Поэтому применить закон сохранения импульса к системе ящик — тележка нельзя. Но так как проекции указанных сил на направление оси х, совпадающей с направлением рельсов, равны нулю, то проекцию импуль­са системы на это направле­ние можно считать постоян­ной, т. е.

Р\х + Р2х = Р'\х + Р2х, (1)

где р_1х и р_2х — проекции

импульса ящика и тележки

с песком в момент падения

ящика на тележку; р'\_х и

P'ix — те же величины после '^^^^^^^^^^^^^^^^^^^

падения ящика. Р_ис. 2

const

г. _ Пусть центр масс сие

Рассматривая тела системы как материальные точки, ] „„,,„„„ „„ ^v

^v ,.\ Ш темы человек—лодка нахо

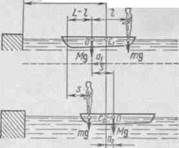
дится на вертикали, прохо­дящей в начальный момент через точку С\ лодки (рис. 3), а после переме­щения лодки — через дру­гую ее точку С2. Так как эта вертикаль неподвижна относительно берега, то искомое перемещение s лодки относительно берега равно перемещению лодки относительно вертикали. А это последнее легко определить по перемещению цен­тра масс О лодки. Как видно из рис. 3, в начальный мо­мент точка О находится на расстоянии а\ слева от верти­кали, а после перехода человека — на расстоянии а2 справа от вертикали. Следовательно, искомое перемеще­ние лодки s = а.\ + а2. Для определения а.\ и а2 воспользуемся тем, что ре­зультирующий момент сил, действующих на систему от­носительно горизонтальной оси, перпендикулярной про­дольной оси лодки, равен нулю. Поэтому для начального положения системы Mgat = mg(l — ai), откуда а\ = ml/(M + m). После перемещения лодки Mgd2 = mg(L — d2 — t), от­куда a2 = m{L — l)/{M + m). Подставив полученные выражения щ и а2 в шдем

выразим в равенстве (1) импульсы тел через их массы" ^м

и скорости, учитывая, что р_2х=0 (тележка до взаимодей­ствия с ящиком покоилась), а также что после взаимо­действия оба тела системы движутся с одной и той же скоростью и:

mivu = {m\ + m₂)u,

или

mi

vi cosa= (mi + m₂) «,

Рис. 3

где v\ — модуль скорости ящика перед падением на те­
лежку; Uu=uicosa — проекция этой скорости на ось х.
Отсюда и= ntiVi cosa/(mi + m₂). (2)

Модуль скорости v\ определим из закона сохранения энергии:

migh = ^l/₂m_lvu

где h = I sin a, откуда

|-V2g7

ms

^^^^^^^^^ v\ =-\J 2gls'ma. Подставив выражение vi в формулу (2), получим

sin a cos a

mi + m₂ После вычислений найдем

20л/2-9,81-2 sin ЗУ ₃0° м/с =

" 20 + 80

= 0,2л/Тэ^6 • 0,867 м/с = 0,767 м/с.

(1),

1 +

(L — /), или S;

м-

М + т

М + т

Пример 4.На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой т. На какое расстояние s удалится лодка от берега, если человек перейдет с кормы; на нос лодки? Силами трения и сопротивления пре­небречь. ^^^^^^^^^^^^^^^^^^^^

Решение. Систему человек — лодка относительной горизонтального направления можно рассматривать ^каЧ Пример 5. При выстреле из пружинного пистолета замкнутую. Согласно следствию из закона сохраненияЯвертикально вверх пуля массой т=20 г поднялась на импульса, внутренние силы замкнутой системы тел неи_Высоту f_l==r_{) M} Определить жесткость k пружины писто-

могут изменить положение центра масс системы. Приме няя это следствие к системе человек — лодка, можне считать, что при перемещении человека по лодке центр масс системы не изменит своего положения, т.е. оста*гЯк „„„ „„ „„„„ „„„„„„ д»ак как на тела системы действуют только консегжятип нется на прежнем расстоянии от берега ^^ у 1ми к-иш-ервагив

^,„₁«^_Лета^ _{если она} была сжата на л:=10 см. Массой пру-П^Жины и силами трения пренебречь.

Решение. Рассмотрим систему пружина — пуля.

где 7*1 — кинетическая энергия первого шара до удара; И2 и Г2 — скорость и кинетическая энергия второго шара после удара. Как видно из формулы (1), для определения е надо найти и2. Согласно условию задачи, импульс системы двух шаров относительно горизонтального направления И не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, найдем: ntiVi = m\U\ -\-т2и2\ (2)

Убедившись, что полученная единица является еди ницей жесткости (1 Н/м), подставим в формулу (3) зна-1зы с масса чения величин и произведем вычисления: ■п„^„„------ . 2-0,02-9,81 -5 и , ,„с и/ ---- ТоТТ5---- Н/м = 196 Н/м.

Пример 6. Шар массой ти движущийся горизон тально с некоторой скоростью о«, столкнулся с неподвиж-|ствующие на каждый груз и на блок в ным шаром массой т2. Шары абсолютно упругие, удаАтдельности. На каждый груз действу- ^^^^^^^^^^И вот две силы: сила тяжести и сила упру- обозначать символо*ости (сила натяжения нити). Направим ^эсь х вертикально вниз и напишем для

ные силы, то для решения задачи можно применить за­кон сохранения энергии в механике. Согласно ему полная! механическая энергия Е\ системы в начальном состоянии (в данном случае перед выстрелом) равна полной энер гии Е₂ в конечном состоянии (когда пуля поднялась на высоту Л), т. е.

0)1

где 7*1, Т₂, 111 и Пг — кинетические и потенциальные| энергии системы в начальном и конечном состояниях Так как кинетические энергии пули в начальном и ко нечном состояниях равны нулю, то равенство (1) при

мет вид ^^^^И

(2)

П, = П₂

Примем потенциальную энергию пули в поле сил тяго
тения Земли, когда пуля покоится на сжатой пружине
равной нулю, а высоту подъема пули будем отсчитывать
от торца сжатой пружины. Тогда энергия системы в на­
чальном состоянии будет равна потенциальной энергии
сжатой пружины, т. е. И i = ' /₂kx², а в конечном состоя­
нии — потенциальной энергии пули на высоте h, т. ^Л
ГЬ = mgh. В

Подставив выражения Ш и П₂ в формулу (2), най-^! дем ' /₂kx²=mgh, откуда

k = 2mgh/x². (3)

Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы*:

1 кг-м-с" 1 м

■ 1 м

1 Н/м.

\m]\g][h}

1 кг• 1 м • с

* Единицу какой-либо величины принято этой величины, заключенным в квадратные скобки.

----- г^

прямой, центральный. Какую долю е своей кинетической энергии первый шар передал второму?

Решение. Доля энергии, переданной первым ша­ром второму, выразится соотношением

л г,

(1)

mil иЛ¹

8 =

(3)

rri[V\ m\U\ 1

2 " (3):

2 2 г -

Решим совместно уравнения (2) и

«2

2m\V\

mi-f-m2

Подставив это выражение и₂ в формулу (1) и сократив на vi и mi, получим

2mii>i "| ² 4mim₂

т_г Г 2т₁у₁ "I ² _

(mi + m₂)²

Из найденного соотношения видно, что доля передан­ной энергии зависит только от масс сталкивающихся шаров.

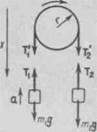Пример 7. Через блок в виде сплошного диска, имею­щего массу т=80 г (рис. 4), перекинута тонкая гибкая нить, к концам которой подвешены гру-ми mi = ЮО г и тг = 200 г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пре­небречь.

Рис. 4

Р е ш е н и е. Рассмотрим силы, дей-

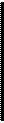каждого груза уравнение движения (второй закон Нью тона) в проекциях на эту ось. Для первого груза

m\g — T\ = rtiia; (1)1

для второго груза

m₂g — Т₂ = пг₂а. (2)

Под действием моментов сил Т{ и Т₂ относительно] оси z, перпендикулярной плоскости чертежа и направлен­ной за чертеж, блок приобретает угловое ускорение ej Согласно основному уравнению динамики вращательного]

движения,

Пг - T\r = J₂e, (3)

где г=а/г; J_z=^l /₂mr² — момент инерции блока (сплош ного диска) относительно оси z.

Согласно третьему закону Ньютона, с учетом невесо­мости нити Т\ = Т\, Т'₂ = Т₂. Воспользовавшись этим, подставим в уравнение (3) вместо Т\ и Г₂ выражения Т и Т₂, получив их предварительно из уравнений (1) и (2) (m₂g — m₂a) r — {m.\g -+- m.\d) r = mr²a/(2r).

После сокращения на г и перегруппировки членов

найдем

а= mi — nix I

Формула (4) позволяет массы m\, m₂ и т выразитв в граммах, как они даны в условии задачи, а ускоре] ние — в единицах СИ. После подстановки числовых зна| чений в формулу (4) получим

(200 - 100) Г „„. , 2_₉оо _м/„2

^й~ (200 + 100 + 80/2) г-⁹'^{81 М/С} ~²'^{88 М/С}"

Пример8. Маховик в виде сплошного диска радиусо» /?=0,2 м и массой т=50 кг раскручен до частоты вра щения П\ = 480 мин^-1 и предоставлен сам себе. Пол действием сил трения маховик остановился через <=50 с! Найти момент М сил трения.

Решение. Для решения задачи воспользуема основным уравнением динамики вращательного движе ния в виде

dL_z = M_zdt, (1

где dL_z — изменение проекции на ось z момента импульсу маховика, вращающегося относительно оси г, совпадаю!

щей с геометрической осью маховика, за интервал вре­мени dt; M_z — момент внешних сил (в данном случае момент сил трения), действующих на маховик относи­тельно оси z.

Момент сил трения можно считать не изменяющимся с течением времени (Mz=const), поэтому интегрирование уравнения (1) приводит к выражению

М_г = М_гМ. (2)

При вращении твердого тела относительно неподвиж­ной оси изменение проекции момента импульса

Д1_г = /_гАо), (3)

где /_г — момент инерции маховика относительно оси г; Аш — изменение угловой скорости маховика.

Приравняв правые части равенств (2) и (3), получим M_ZM= JzAto, откуда

М_г = /_г-^- (4)

Момент инерции маховика в виде сплошного диска определяется по формуле

/_г=7₂т/?².

Изменение угловой скорости Асо = со₂ — <j)i выразим через конечную л₂ и начальную п\ частоты вращения, пользуясь соотношением со = 2лп:

Дю = а>2 — (Oi = 2ля2 — 2лп\ = 2я(п₂—п\).

Подставив в формулу (4) выражения J_z и Асо, полу­чим

M_z = nmR\n₂ — п\)/М. (5)

Проверим, дает ли расчетная формула единицу мо­мента силы (Н-м). Для этого в правую часть формулы вместо символов величин подставим их единицы:

[m][R²][n] 1кг-1м²-1с-' ' _₂ , , „

д_ j i" j t i _------------------------- = 1кг-М-С •1м=1Н-М.

[t] 1с

Подставим в (5) числовые значения величин и произ­ведем вычисления, учитывая, что ti\ = 480 мин^_1 = = 480/60 с^-1 = 8 с-¹:

,. 3,14-50-(0,2)²-(0-8)_u , _u

М_г = —^:---------- \_п -------- i-H-M=— 1 Н-М.

ОО

Знак минус показывает, что момент сил трения ока­зывает на маховик тормозящее действие.

Пример 9.Платформа в виде сплошного диска радиу­сом #=1,5 м и массой т₁=180кг вращается около вертикальной оси с частотой п=10 мин . В центре плат­формы стоит человек массой т₂=60 кг. Какую линейную скорость v относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. Согласно условию задачи, момент внеш­них сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать рав­ным нулю. При этом условии проекция L_z момента им­пульса системы платформа — человек остается по­стоянной:

L_z = J_z(x) = const, (1)

где J_z — момент инерции платформы с человеком отно­сительно оси г; со — угловая скорость платформы.

Момент инерции системы равен сумме моментов инер­ции тел, входящих в состав системы, поэтому в началь­ном состоянии /_z = /i+/2, а в конечном состоянии J'₂ = = Л+/₂.

С учетом этого равенство (1) примет вид

(/i+/г)© = (/!+-/£)<»', . (2)

где значения моментов инерции /₍ и J₂ платформы и человека соответственно относятся к начальному состоя­нию системы; Л и J₂ — к конечному.

Момент инерции платформы относительно оси z при переходе человека не изменяется: J_l = J[ = ^{/₂m\R². Мо­мент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материаль­ную точку, то его момент инерции J₂ в начальном состоя­нии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека J'₂ = m₂R².

Подставим в формулу (2) выражения моментов инер­ции, начальной угловой скорости вращения платформы с человеком (со = 2лп) и конечной угловой скорости (со' = и//?, где v — скорость человека относительно пола): С/2ГГЦЯ² + 0)2лп = ('/г/л,/?² + m₂R²)v/R.

После сокращения на R² и простых преобразований находим скорость:

v = 2nnRm_i/(m[ -\-2т₂).

Произведем вычисления:

2-3,Н~-1,5-180
^V =------- 180 + 2-60 М/С=1м/С.

Пример 10.Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости v\, сообщенной ракете при запус­ке, она удалится от поверхности на расстояние, равное радиусу Земли (/? = 6,37-10⁶ м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.

Решение. Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При не­работающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно,

Г, + П, = Г_г + П₂, (1)

где Т\, Tli и Т₂, Пг — кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, рав­ном радиусу Земли) состояниях.

Согласно определению кинетической энергии,

T_l = */₂mv².

Потенциальная энергия ракеты в начальном со­стоянии*

П, = — GmM/R.

По мере удаления ракеты от поверхности Земли ее потенциальная энергия возрастает, а кинетическая — убывает. В конечном состоянии кинетическая энергия Т₂ станет равной нулю, а потенциальная — достигнет макси­мального значения:

Yl₂=-GmM/(2R).

Подставляя выражения Т_и П_ь Т₂ и Пг в (1), получаем

mv\/2 — GmM/R = —GmM/(2R),

откуда

* Потенциальная энергия гравитационного взаимодействия тел. бесконечно удаленных друг от дуга, принимается равной нулю.

Г

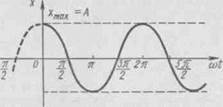
График соответствующего гармонического колебания приведен на рис. 5.

где со

Заметив, что GM/R² = g (g — ускорение свободного па­дения у поверхности Земли), перепишем эту формулу

в виде

vi = -yfgR,

что совпадает с выражением для первой космической скорости.

Произведем вычисления:

у, _{= Л}/9,8-6,37.10" м/с = 7,9 км/с.

Xmax = 1 MM. начертить их

Пример 11.Точка совершает гармонические колеба­
ния с частотой v= 10 Гц. В момент, принятый за началь­
ный, точка имела максимальное смещение
Написать уравнение колебаний точки
график. ^^^^^^^^^^^м

Решение. Уравнение колебаний точки можно за­писать в виде

x = Asin(a>t +ф0, (1)

где А — амплитуда колебаний; со — циклическая частота;
t — время; ф1 — начальная фаза. .

По определению, амплитуда колебаний

■Л = Хщах. \£)

Циклическая частота со связана с частотой v соот­ношением

о) = 2лл>. (3)

Для момента времени t = Q формула (1) примет вид

Xmax=/4sin<pi,

откуда начальная фаза

ф1 = arcsin(x_max/v4) = arcsin l,

или

q>,= (2ft+l)n/2(* = 0, 1,2,...).

Изменение фазы на 2я не изменяет состояния коле­блющейся точки, поэтому можно принять

_Ф1 = я/2. (4)

С учетом равенств (2) — (4) уравнение колебаний примет вид

x = Asin{2nxt-\-<p), или x=Acos2nvt,

м, v= 10 Гц, ф = я/2.

где А = 1 мм= 10

Рис. 5

Пример 12.Частица массой т = 0,01кг совершает гармонические колебания с периодом Т—2с. Полная энергия колеблющейся частицы £ = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы £тах, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

£ = ' 1чпал''А², 2л/Т. Отсюда амплитуда

2Е_ т

(1)

2л V

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F=—kx, где k — коэффициент квазиупругой силы; х — смещение колеблющейся точки. Максимальной сила бу­дет при максимальном смещении л:_тах, равном амплитуде:

F_max=kA. (2)

Коэффициент k выразим через период колебаний:

к = та>²=т-4л²/Т². (3)

Подставив выражения (1) и (3) в (2) и произведя упрощения, получим

-« max = 2nsj2mE/T.

Произведем вычисления:

мм;

^А=wrV^¹"=°-^{045 м}=⁴⁵

Начальную фазу результи­рующего колебания можно также определить непосред­ственно из векторной диа­граммы (рис. 6):

A, sin cpi 4- Azsmip? w= arctg—;-------- ——.------------------------ — T ° /l|COS9i + /l2COS(p2

Произведем вычисления:

Рис. 6

^ = V32+22+2-3-2cos(60°— 30°) cm = 4,84 cm; 3 sin 30° + 2 sin 60°

F_raax = -^!^-V2-l(r²-l(r⁴ Н= 4,44- Ю-³ Н= 4,44 мН.

Пример 13.Складываются два колебания одинако­вого направления, выраженные уравнениями

Xi = AiCos~(t+T\); X2 = A₂cos-j-(t +т₂),

где Л1 = 3см, Л₂ = 2см, xi = l/6c, т₂=1/3с, 7""= 2 с. Построить векторную диаграмму сложения этих колеба­ний и написать уравнение результирующего колебания. Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно век­торную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к канонической форме х= A cos ((at-{-(f), получим

. / 2я , , 2я \ . / 2л , , 2л \

*i=^icos( — Н—y~^x4 ' *2 = ^₂cos( — Н—f-та) .

Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту

ю = 2я/7\

Начальные фазы первого и второго колебаний соот­ветственно равны

2л 2л

ф1=— Ti; ф2 = — Т2.

Произведем вычисления:

со^^^с-^З.Нс-¹;

_?,=-|)рад=30°; _ф2 = -|--1_рад=60^о.

Изобразим векторы Ai и А₂. Для этого отложим от­резки длиной >4i = 3cm и Л₂ = 2см под углами ф1 = 30° и ф₂ = 60° к оси Ох. Результирующее колебание будет происходить с той же частотой w и амплитудой А, равной геометрической сумме амплитуд A_t и А₂: A = Ai+A₂. Согласно теореме косинусов,

А = л/Л 1 + Л| + 2ЛИ₂со8(ф₂—Цц) .

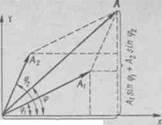
Ф= arctg

3 cos 30° + 2 cos 60°

arctg0,898 = 42°,

или ф= 0,735 рад.

Так как результирующее колебание является гармо­ническим, имеет ту же частоту, что и слагаемые колеба­ния, то его можно записать в виде

х= А соэ(со^ + ф),

где Л = 4,84см, о) = 3,14с^-1, ф=0,735рад.

Пример 14.Плоская волна распространяется вдоль прямой со скоростью v = 20 м/с. Две точки, находя­щиеся на этой прямой на расстояниях Xi=12m и *2 = = 15 м от источника волн, колеблются с разностью фаз Аф=0,75я. Найти длину волны к, написать уравнение волны и найти смещение указанных точек в момент /=1,2 с, если амплитуда колебаний Л = 0,1 м.

Решение. Точки, находящиеся друг от друга на расстоянии, равном длине волны X, колеблются с разно­стью фаз, равной 2л,; точки, находящиеся друг от друга на любом расстоянии Л*, колеблются с разностью фаз, равной

Дф= Дх-2я/А. = (л;₂ — Х\)'2л/Х.

Решая это равенство относительно к, получаем

Х=2л(х₂—дгО/Аф. (Г)

Подставив числовые значения величин, входящих в выражение (1), и выполнив арифметические действия,

получим

X = JM^_m = 8m. 0,75л

Для того чтобы написать уравнение плоской волны, надо еще найти циклическую частоту to. Так как ы = = 2л/Г (T = X/v — период колебаний), то

ы = 2nv/k.

Произведем вычисления:

2л-20 _i r -1-с = 5я с .

Зная амплитуду А колебаний, циклическую частоту со и скорость v распространения волны, можно написать уравнение плоской волны для данного случая:

y = Acos(o(t—x/v), (2)

где Д = 0,1 м, со = 5я с^-1, и = 20 м/с.

Чтобы найти смещение у указанных точек, доста­точно в уравнение (2) подставить значения t и х:

yi = 0,lcos5n(l,2— 12/20) м = 0,1 cosЗлм= — 0,1 м;

«/₂ = 0,1 cos5я( 1,2—15/20) м = 0,1 соэ2,25я м =

= 0,1 cos 0,25ям = 0,071 м=7,1 см.