Молек-ая физика. Предмет молек-ой физики. Функции распределения Максвелла молекул идеального газа, их свойства. Среднеквадратичная и вероятная скорости
МФ и термод-ка имеют один и тот же предмет изучения, они изучают макротела, и процессы протекающие в них. Имея один и тот же предмет изучения МФ и термод-ка используют различные методы. В основе метода МФ лежит представление о том, что все макро тела состоят огромного числа микрочастиц, атомов или молекул, находящиеся в непрестанном хаотичном движении. Все процессы протек-ие в макро телах обусловлены совокупленным действием огромного числа этих атомов или молек-л. В конечном счете в МФ макроскопические пар-ры (давление, темп-ра, объем) выводятся через усредненные динамические хар-ки микрочастиц (скорость, импульс, энергия)., при этом используются статические законы. В термод-ке нерасматрив-ся строение вещ-ва, она изучает состояние равновесия макросистемы и пути перехода м/у этими состояниями, термод-ка основывается на фундаментальных обычным путем установ-ых законных- началах тер-ки. Состояние терм-кого равновесия макросистем описывается термод-ми пар-ми (дав-ие, объем, температура). Любой процесс рассм-ся как переход из одного состояния равновесия в другое. Любой переход сопровождается изменением хотяб одного термод-ого пар-ра. Имея раз-ые методы МФи тер-ка взаимодополняют друг друга образуя единое целое, здесь так же используют физич-ие модели – модель идеального газа, она строится на трех допущениях: размеры не имеют значения, атомы и мол-лу не взаимод-ют, они сталкиваются со стенками сосуда абсол-но упруго. Реальные газы при низких давлениях и высоких температурах близки к идеал-м. Законы идеал-ого газа: 1) Бойля-Марриота- темпер-ра неизменна, изотер-ий процесс; 2) Гей-Люссака- изохорный, при постоянном объеме; 3) изобарный, при неизменном давлении газа. Закон Авогадро: При одинаковых условиях 1 моль любого газа занимает одинаковый объем; В одном моле любого вещ-ва содержится одинаковое число молекул. Закон Дальтона: Давление смеси газов, равно сумме порциональных давлений каждой составляющей в отдельности. 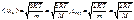
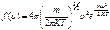 .
. 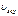 явл-ся фун-ей Т, с ростом Т, она возрастает.
явл-ся фун-ей Т, с ростом Т, она возрастает.
18) Применение распределения Максвелла для расчета давления газа на стенку сосуда, средней энергии, приход-ся на одну степень свободы, и внутренней энергии идеального газа.
Число степеней свободы- число независимых параметров полностью опред-их ее состояние. 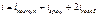 Средней энергии, приход-ся на одну степень свободы:
Средней энергии, приход-ся на одну степень свободы: 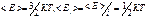 . Закон Больцмана по распред-ию степеней свободы: речь идет о среденей энергии прих-ся на одну степень свободы
. Закон Больцмана по распред-ию степеней свободы: речь идет о среденей энергии прих-ся на одну степень свободы 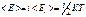 - средняя энергия произвольной молекулы идеального газа. Внут-яя энергия идеального газа для одной молекулы:
- средняя энергия произвольной молекулы идеального газа. Внут-яя энергия идеального газа для одной молекулы: 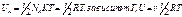 . Рассмотрим переход системы из одного состояние в другое:
. Рассмотрим переход системы из одного состояние в другое: 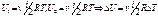 , изменение внутренней энергии не зависит от пути перехода м/у начальным и конечным состоянием, а значит внутренняя энергия яв-ся ф-цией состояния термодин-ой системы.
, изменение внутренней энергии не зависит от пути перехода м/у начальным и конечным состоянием, а значит внутренняя энергия яв-ся ф-цией состояния термодин-ой системы.
23) Удельная и молярная теплоемкость. Расчет Cp,Cv.
Удельная теплоемкость: 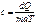 , молярная теплоемкость:
, молярная теплоемкость: 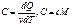 . При изохорном процессе:
. При изохорном процессе: 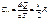 , при изобарном:
, при изобарном: 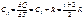 ,
, 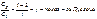 . Теплоемкость газа не зависит от его Т, опыт показывает, что существует сложная зависимость теплоемкости от температуры. При низких Т и колеб-ые и вращ-ые движение молекул заморожено, она движется только поступательно; при комнатных Т, вместе с пос-м движ-м учавствует и вращательное движение; ну а при высоких Т, возможно все.
. Теплоемкость газа не зависит от его Т, опыт показывает, что существует сложная зависимость теплоемкости от температуры. При низких Т и колеб-ые и вращ-ые движение молекул заморожено, она движется только поступательно; при комнатных Т, вместе с пос-м движ-м учавствует и вращательное движение; ну а при высоких Т, возможно все.
24) Адиабатические и политропические процессы. Вывод ф-лы Пуссона. Сравнение изотермы и адиабаты.
Политропные процессы- процессы протекающие при какой-либо постоянной теплоемкости. 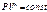 - ур-ие политропов, n- показатель политропы =
- ур-ие политропов, n- показатель политропы = 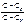 ,
, 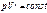 - адиаб-ий процесс,
- адиаб-ий процесс, 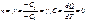 . Изотер-ий процесс: n=1, при с стрем-ся к бесконечности, б.б теплоемкость означает, что какое бы ни ыло большое кол-во теплоты не сооб-ое бы системе, ее температура постоянна. Изобарный: n=0, давление постоянно. Изохорный: n= бесконечность, объем константа. Каждый из рассмотренных изопроцессов протекает при какой-либо const теплоемкости, а значит все эти процессы яв-ся политропными. Рассмотрим адиабатный процесс:
. Изотер-ий процесс: n=1, при с стрем-ся к бесконечности, б.б теплоемкость означает, что какое бы ни ыло большое кол-во теплоты не сооб-ое бы системе, ее температура постоянна. Изобарный: n=0, давление постоянно. Изохорный: n= бесконечность, объем константа. Каждый из рассмотренных изопроцессов протекает при какой-либо const теплоемкости, а значит все эти процессы яв-ся политропными. Рассмотрим адиабатный процесс: 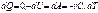
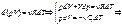
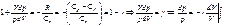
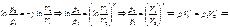
Т.к. начальные и конечные состояния выбраны произвольно, то 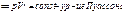 .
.
26) Нер-во Клаузиуса. Энтропия, и ее св-ва. Статический смысл энтропии и ее расчет. Третье начало тер-ки.
Впервые понятие было введено в 1865г. нем-им ученым Клаузиусом при изучении равновесных изотермических процессов, для этого он ввел понятие приведенного кол-ва теплоты равное теплоте переданной системе к Т тела передающего эту теплоту dQ/T. Энтропия – ф-ция состояния сист-мы полный диф-л которой приведены теплотой. Для любой ф-ции состояние имеет смысл лишь изменения это ф-ции при каком-то конечном переходе. 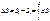
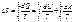 Клаузиус показал, что для обратимых процессов dQ/T=const, для необратимых поцессов энтропия всегда возрастает ΔS>0. При любых процессах энтропия системы не убывает ΔS>0- нерав-во Клаузиуса.
Клаузиус показал, что для обратимых процессов dQ/T=const, для необратимых поцессов энтропия всегда возрастает ΔS>0. При любых процессах энтропия системы не убывает ΔS>0- нерав-во Клаузиуса.
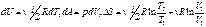 . При адиабатном процессе энтропия постоянна, и поэтому это процесс называют изоэнтропийным процессом. Третье начало тер-ки: не первое, не второе не показывают как ведет себя энтропия при Т стрем-ся к нулю, на это отвечает третье начало тер-ки, при
. При адиабатном процессе энтропия постоянна, и поэтому это процесс называют изоэнтропийным процессом. Третье начало тер-ки: не первое, не второе не показывают как ведет себя энтропия при Т стрем-ся к нулю, на это отвечает третье начало тер-ки, при 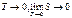 - теорема Нернет Планка.
- теорема Нернет Планка.
19) Распределение Больцмана. Распределение молекул атмосферы в гравитац-ом поле земли. Барометрическая ф-ла. Распределение Максвелла-Больцмана.
При выводе распеределения молекул по скоростям Максвелл не учитывал тот факт, что все молекулы находятся в гравитационном, потенциальном поле притяжении земли, 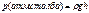 , При изменении
, При изменении 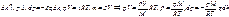
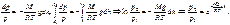
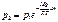
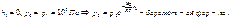 Позволяет по известной высоте рассчитать давление или наоборот.
Позволяет по известной высоте рассчитать давление или наоборот. 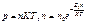 - распред-ие молек-л по высоте Больцмана, расп-ие Максвелла:
- распред-ие молек-л по высоте Больцмана, расп-ие Максвелла: 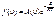 , ф-ция расп-ия Максвелла-Больцмана:
, ф-ция расп-ия Максвелла-Больцмана: 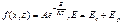
20) Явления переноса. Понятие и расчет среденей длины свободного пробега молекул. Время релаксации. Внутреннее трение, и ее коэф-нт.
В терм-ке в неравновесных системах происходят необратимые процессы, обусловленные переносом энергии, массы, импульса. Процесс обусл-ый переносом энергии называется теплопроводностью, перенос импульса- внутренним трением или вязкостью, перенос массы- диффузией.
Вязкость или внутреннее трение: Вязкость возникает м/у парал-но движущимися с различными скоростями слоя, и обусловлено тем, что молекулы из более быстрого слоя проникают в более медленный слой ускоряя его, и наоборот. Математически отображается законом Ньютона- 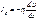 , поток импульса переносимым в 1-цу времени, через един-юу поверхность в направлении перпендик-ой этой поверхности-
, поток импульса переносимым в 1-цу времени, через един-юу поверхность в направлении перпендик-ой этой поверхности- 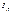 ,
, 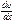 - градиент скорости, равен быстроте изменения скорости в заданном направлении,
- градиент скорости, равен быстроте изменения скорости в заданном направлении, 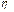 - коэф-ент вязкости, равный потоку импульса при 1-ом градиенте скорости, «-» - импульс передается от более быстрых слоев к менее быстрых слоев.
- коэф-ент вязкости, равный потоку импульса при 1-ом градиенте скорости, «-» - импульс передается от более быстрых слоев к менее быстрых слоев. 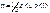 . Молекулы газа- хаотичны, и непрер-но сталкиваются м/у собой, расстояние которое пролетает молекула м/у двумя последующими столкновениями- длина свободного пробега. Т.к. молекул много следует говорить только о средене величине свободного пробега
. Молекулы газа- хаотичны, и непрер-но сталкиваются м/у собой, расстояние которое пролетает молекула м/у двумя последующими столкновениями- длина свободного пробега. Т.к. молекул много следует говорить только о средене величине свободного пробега 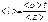 , где <z>- среднее число столкновений. Для определения средней длины свободного пробега опреде-ют <z>, для его определения вводится величина эффективным диаметром молекулы. Эффект-ым диаметром молекул называют минимальное расстояние м/у центрами масс молекул на которое они сближаются при сталкивании. Эф-ть диам-р молекул зависит от скорости теплового движения молекулы, и от температуры газа.
, где <z>- среднее число столкновений. Для определения средней длины свободного пробега опреде-ют <z>, для его определения вводится величина эффективным диаметром молекулы. Эффект-ым диаметром молекул называют минимальное расстояние м/у центрами масс молекул на которое они сближаются при сталкивании. Эф-ть диам-р молекул зависит от скорости теплового движения молекулы, и от температуры газа. 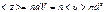 . При выводе данной фор-лы считалось, что все остальные молекулы, кроме рассматриваемой, покоятся, когда те находятся в непрестанном движении, то
. При выводе данной фор-лы считалось, что все остальные молекулы, кроме рассматриваемой, покоятся, когда те находятся в непрестанном движении, то 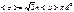 .
. 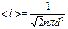
25) Обратимые и необратимые процессы. Второе начало тер-ки. Форм-ки Кельвина и Клаузиуса. КПД, и цикл Карно.
Круговыми процессами (циклы)- процессы, при которых система пройдя ряд промеж-ых состояний возвращается в исходное состояние. Если работа >0, то процесс протекает по часовой стрелке и называется прямым. В противном случае обратным. Прямые процессы используются в тепловых двигателях, обратные в холодильных установках. Процесс называется обратимым, если при переходе с начала в прямом, а затем в обратном направлении, система возвр-ся в исходное состояние и при этом ни в самой системе, ни в окр-ей среде не происходит ни каких изменений, все остальные процессы- необратимы. Обратимыми могут быть только равновесные процессы, при которых система последовательно проходит через ряд термод-их равновесий. Равновестными можно рассматривать квазистатические процессы- скорость протекания которых очень мала. Обратимые процессы явл-ся идеализацией реальных процессов, то они играют огромную роль в ТД, т.к. обладают наиб-м КПД, поэтому на практике реальные процессы стремятся к max приблизиться к обратимым. Все это относится лишь к замкнутым процессам. Клаузиус показал, что для обратимых процессов dQ/T=const, для необратимых поцессов энтропия всегда возрастает ΔS>0. При любых процессах энтропия системы не убывает ΔS>0- нерав-во Клаузиуса, и отображает одну из трактовок второго начала тер-ки: любые реальные процессы сопровождаются возрастанием энтропии. Определение по Кельвину: Невозможен круговой процесс, единственным результатом которого было бы преобразование, теплоты полученной от нагревателя в эквивалентную ей работу. По Клаузиусу: Невозможен круговой процесс, единственным результатом которого было бы предача теплоты от менее нагретого тела, к более нагретому. В отличии от первого нач-ла терм-ки, которое показало какие процессы возможны, а какие нет, второе нач-ло тер-ки показало в каком направлении могут протекать эти процессы. След-ие: невозможно построить вечный двишатель второго рода . Фран-им Карно бало док-но, что из всех воз-ых циклах при одинак-ых Т нагревателей, и Т одинаковой холодильников, наиб-ая КПД обладает цикл протекающий по двум изотермам и двум адиабатам.
27) Объединенный закон тер-ки. Свободная и связанная энергия. Свободная энергия Гибба. Энтальпия. Ур-ие Гельмгольца.
Ф-ция представляющая собой сумму или разность ф-ций состояния так же яв-ся ф-цией состояния. 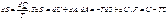
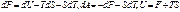 . Внутренняя энергия идеального газа состоящая из двух частей из свободной энергией F и связной TS. Только свободная энергия может быть реализована в виде работы, связная энергия называется обесцененной, таким образом энтропию можно представить, как меру обесценности внутренней энергии.
. Внутренняя энергия идеального газа состоящая из двух частей из свободной энергией F и связной TS. Только свободная энергия может быть реализована в виде работы, связная энергия называется обесцененной, таким образом энтропию можно представить, как меру обесценности внутренней энергии.
21) Диффузия и теплопроводность, их коэффициенты, о них же в газах и твердых телах. Понятие о явлении переноса в разряженных газах. Эффузия.
Теплопроводность: если привести в соприкосновение газы с различными Т, то через некоторое время разность Т вырав-ся, объясняется тем, что в результате столкновений молекулы с большей энергией передают какую то ее часть, молекулой с меньшей энергией, математически этот процесс изображается законом Фурье: 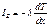 , плотность потока энергии численно равно энергии переносимой через единичную площадку в 1-цу времени в направлении перпендик-ой к данной площадке-
, плотность потока энергии численно равно энергии переносимой через единичную площадку в 1-цу времени в направлении перпендик-ой к данной площадке- 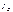 ,
, 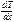 - градиент температуры, численно равен скорости изменения Т, в заданном направлении,
- градиент температуры, численно равен скорости изменения Т, в заданном направлении, 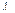 - коэф-ент теплопров-ти равный потоку энергии при ед-ом градиенте, «-» - указывает на то, что энергия переносимая от газа с более высокой Т, к газу более низкой.
- коэф-ент теплопров-ти равный потоку энергии при ед-ом градиенте, «-» - указывает на то, что энергия переносимая от газа с более высокой Т, к газу более низкой. 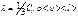 . Явлен-ие диффузии: обусловлено взаимопроникновением молекул соприкасающихся веществ. Математи-ки отображ-ся законом Фика:
. Явлен-ие диффузии: обусловлено взаимопроникновением молекул соприкасающихся веществ. Математи-ки отображ-ся законом Фика: 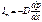 ,
, 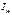 - поток массы численно равен массе переносимой в 1-цу времени через 1-ую площадку, в направлении перпен-ой к этой площадке,
- поток массы численно равен массе переносимой в 1-цу времени через 1-ую площадку, в направлении перпен-ой к этой площадке, 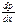 - градиент давления числено равный скорости изменения давления в заданном направлении, D- коэф-нт диф-и, равный потоку массы при ед-ом градиенте, «-» - масса переносится о вещ-ва с большим давлением, к вещ-ву с меньшим давлением.
- градиент давления числено равный скорости изменения давления в заданном направлении, D- коэф-нт диф-и, равный потоку массы при ед-ом градиенте, «-» - масса переносится о вещ-ва с большим давлением, к вещ-ву с меньшим давлением.