Допускаемая удельная окружная сила
ЛЕКЦИЯ 13
Ременные передачи
Скольжение ремня
Два вида скольжения ремня по шкиву: упругое - неизбежное при нормальной работе передачи; буксирование - при перегрузке.
Когда ремень обегает ведущий шкив, его натяжение падает от 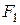 до
до 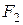 (рис. 18.6), ремень укорачивается и отстает от шкива - возникает упругое скольжение.
(рис. 18.6), ремень укорачивается и отстает от шкива - возникает упругое скольжение.
Когда ремень обегает ведомый шкив натяжения ремня возрастает от 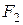 до
до 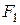 , он удлиняется и опережает шкив.
, он удлиняется и опережает шкив.
Упругое скольжение ремня происходит не на всей дуге обхвата, а лишь на ее части - дуге скольжения 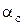 , которая всегда располагается со стороны сбегания ремня со шкива. Со стороны набегания ремня на шкив имеется дуга покоя
, которая всегда располагается со стороны сбегания ремня со шкива. Со стороны набегания ремня на шкив имеется дуга покоя 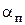 , на который сила в ремне не меняется, оставаясь равной натяжению набегающей ветви.
, на который сила в ремне не меняется, оставаясь равной натяжению набегающей ветви.
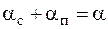 , (18.12)
, (18.12)
где a - дуга обхвата ремнем шкива.
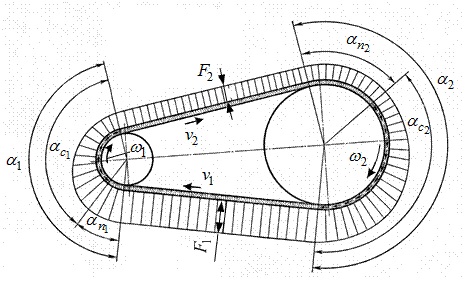
Рис. 18.6. Скольжение в ременной передаче
Упругое скольжение ремня неизбежно в ременной передаче, оно возникает в результате разности натяжений ведущей и ведомой ветвей.
По мере роста 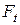 уменьшается дуга покоя
уменьшается дуга покоя 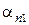 , следовательно уменьшается запас сил трения. При значительной перегрузке
, следовательно уменьшается запас сил трения. При значительной перегрузке 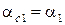 и ремень скользит по всей поверхности касания с ведущим шкивом - буксует. Упругое скольжение ремня характеризуется коэффициентом скольжения e
и ремень скользит по всей поверхности касания с ведущим шкивом - буксует. Упругое скольжение ремня характеризуется коэффициентом скольжения e
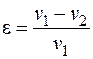 , (18.13)
, (18.13)
где 
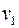 и
и 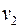 - окружные скорости ведущего и ведомого шкивов. При нормальном режиме работы
- окружные скорости ведущего и ведомого шкивов. При нормальном режиме работы 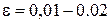 .
.
Вследствие упругого скольжения 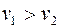 и передаточное отношение i ременной передачи имеет некоторое непостоянство
и передаточное отношение i ременной передачи имеет некоторое непостоянство
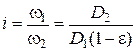 . (18.14)
. (18.14)
Напряжения в ремне
Вследствие того, что при работе ременной передачи усилия в ветвях различны, то и напряжения по длине ремня распределяются неравномерно (рис. 18.7).
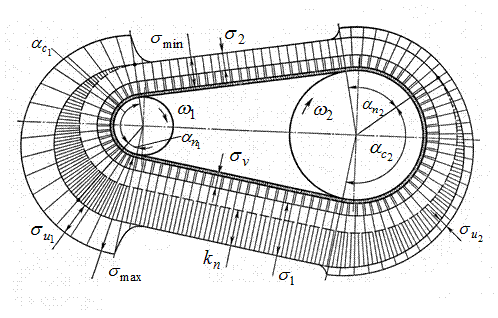
Рис. 18.7. Эпюра напряжений в ремне при работе передачи
В ремне возникают следующие напряжения.
1. Предварительное напряжение 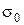
При холостом ходе каждая ветвь натянута с силой 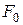 , и испытывает деформацию осевого растяжения-сжатия, тогда
, и испытывает деформацию осевого растяжения-сжатия, тогда
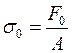 , (18.15)
, (18.15)
где A - площадь поперечного сечения ремня. Из условия долговечности рекомендуется:
· для плоских ремней 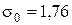 МПа;
МПа;
· для клиновых ремней 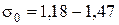 МПа.
МПа.
2. Полезное напряжение 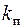 (удельная окружная сила)
(удельная окружная сила)
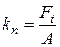 или
или 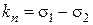 , (18.16)
, (18.16)
где 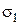 - напряжение ведущей ветви
- напряжение ведущей ветви 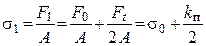 ;
;
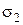 - напряжение ведомой ветви
- напряжение ведомой ветви 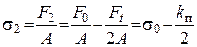 .
.
Величиной 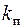 оценивается тяговая способность ременной передачи.
оценивается тяговая способность ременной передачи.
3. Напряжение изгиба 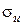 .
.
Возникает в ремне при огибании им шкивов (рис. 18.8). Считая, что ремень испытывает деформацию чистого изгиба, используем закон Гука:
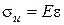 , (18.17)
, (18.17)
где 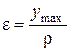 - относительное удлинение волокон в растянутой зоне при изгибе;
- относительное удлинение волокон в растянутой зоне при изгибе; 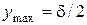 - максимальное расстояние от нейтральной линии до крайнего волокна;
- максимальное расстояние от нейтральной линии до крайнего волокна; 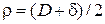 - кривизна ремня по нейтральному слою.
- кривизна ремня по нейтральному слою.
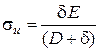 . (18.18)
. (18.18)
Величиной d в знаменателе пренебрегаем по сравнению с D и получаем
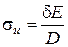 , (18.19)
, (18.19)
где E - модуль упругости ремня.
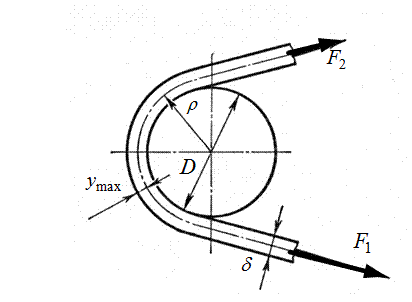
Рис. 18.8. К изгибу ремня на шкиве
Из формулы следует, что на малом шкиве напряжение изгиба будет большим. 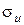 изменяется по отнулевому циклу и является главной причиной усталостного разрушения ремня.
изменяется по отнулевому циклу и является главной причиной усталостного разрушения ремня.
Напряжение изгиба не влияет на тяговую способность ремня.
4. Напряжение от центробежных сил 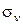 :
:
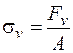 . (18.20)
. (18.20)
Наибольшее суммарное напряжение 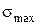 возникает в поперечном сечении ремня в месте его набегания на малый шкив. Оно сохраняется по всей дуге покоя.
возникает в поперечном сечении ремня в месте его набегания на малый шкив. Оно сохраняется по всей дуге покоя.
Кривые скольжения
Тяговая способность ременной передачи обуславливается сцеплением ремня со шкивами.
Исследуя тяговую способность, строят графики - кривые скольжения и КПД (рис. 18.9); на базе этих графиков разработан метод расчета ременных передач.
По оси абсцисс графика откладывают нагрузку, выраженную через коэффициент тяги j
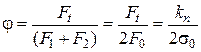 (18.21)
(18.21)
По оси ординат коэффициент скольжения - e и к.п.д. - h;
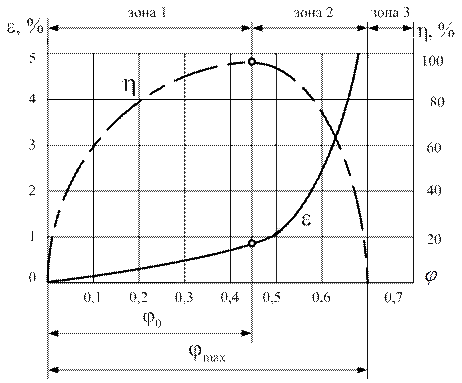
Рис. 18.9. Кривые скольжения и к. п. д.
В зоне, где 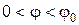 наблюдается упругое скольжение. В этой зоне упругие деформации ремня подчиняются закону Гука.
наблюдается упругое скольжение. В этой зоне упругие деформации ремня подчиняются закону Гука.
При 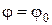
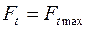 .
.
При 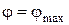 , работа передачи становится неустойчивой, появляется частичное буксирование, КПД падает, ремень быстро изнашивается.
, работа передачи становится неустойчивой, появляется частичное буксирование, КПД падает, ремень быстро изнашивается.
При 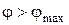 - наступает полное буксирование, ведомый шкив останавливается,
- наступает полное буксирование, ведомый шкив останавливается, 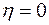 . Т. е. коэффициент тяги j надо принимать близким или равным
. Т. е. коэффициент тяги j надо принимать близким или равным 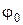 , которому соответствует
, которому соответствует 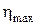 .
.
Значение 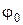 устанавливается экспериментально, для каждого типа ремня. Т. е. критерием рациональной работы ремня служит коэффициент тяги
устанавливается экспериментально, для каждого типа ремня. Т. е. критерием рациональной работы ремня служит коэффициент тяги 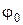 , величина которого определяет допускаемую окружную силу
, величина которого определяет допускаемую окружную силу 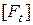 :
:
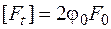 . (18.22)
. (18.22)
Допускаемая удельная окружная сила
Допускаемая приведенная удельная окружная сила в ремне определяется по формуле:
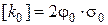 . (18.23)
. (18.23)
Она зависит от типа ремня, его толщины, диаметра шкива  , скорости ремня и предварительного напряжения
, скорости ремня и предварительного напряжения  . Значение
. Значение 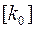 получают в результате обработки многочисленных кривых скольжения.
получают в результате обработки многочисленных кривых скольжения.
Расчет ременной передачи ведут по допускаемой удельной окружной силе 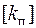 :
:
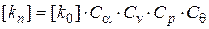 , (18.24)
, (18.24)
где 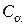 - коэффициент угла обхвата;
- коэффициент угла обхвата; 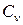 - скоростной коэффициент;
- скоростной коэффициент; 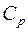 - коэффициент нагрузки и режима работы;
- коэффициент нагрузки и режима работы; 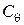 - коэффициент, учитывающий вид передачи и ее расположение.
- коэффициент, учитывающий вид передачи и ее расположение.
Виды разрушения ремня
Усталостное разрушение
При изгибе ремня возникает внутреннее трение между слоями ремня, которое при циклическом изменении приводит к усталостному разрушению.
Перегрев ремня
Температура возникает в результате упругого скольжения и внутреннего трения. Перегрев отрицательно влияет на физико-механические свойства ремня и срок его службы.
Износ ремня
Возникает вследствие упругого скольжения и частичного буксирования.
