При вращательном движении все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения

Рис. 1.

Виды механического движения: 1а) поступательного; б) вращательного.

Окружности, описываемые точками, находятся в плоскостях, перпендикулярных оси вращения (рис. 1б). Ось вращения может находиться как внутри тела, так и вне его.

Чтобы твёрдое тело с закреплённой осью привести во вращательное движение, необходимо хотя бы в одной из его точек приложить внешнюю силу 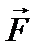, не проходящую через ось вращения и непараллельную ей, другими словами, чтобы эта сила создавала момент силы.

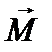
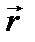Моментом силы относительно произвольной точки О (неподвижного начала) называется векторное произведение радиуса-вектора , проведенного из этой точки к точке приложения силы, на силу :

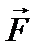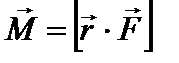(3)

Момент силы 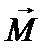перпендикулярен к плоскости, в которой лежат радиус-вектор 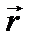и сила 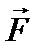, и образует с ними правую тройку (при наблюдении с конца вектора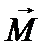 видно, что вращение по кратчайшему пути от 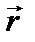к 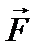происходит против часовой стрелки (рис. 2).

Рис. 2.

К определению момента силы относительно оси вращения

Модуль вектора 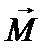согласно определению векторного произведения равен

M = r F sin ( ) = r F sin α = F l ,

(4)

где l = r sin α – длина перпендикуляра, опущенного из точки C на прямую, вдоль которой действует сила, называется плечом силы (рис. 2).

Моментом инерции I материальной точки относительно некоторой оси называется скалярная величина, равная произведению массы материальной точки m_i на квадрат расстояния r_i от этой точки до оси вращения

.

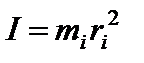(5)

Момент инерции I твёрдого тела относительно той же оси

,

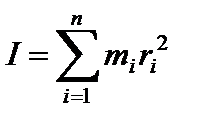(6)

где m_i и r_i - масса i-той материальной точки и её расстояние до оси вращения.

Момент инерции зависит не только от массы всего тела и её распределения в теле, но также от его ориентации относительно оси вращения и является величиной аддитивной.[1]

При непрерывном распределении массы относительно оси вращения, момент инерции равен:

.

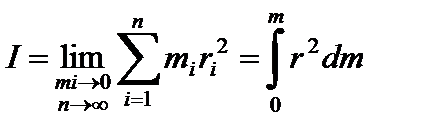(7)

Учитывая, что dm = ρ dV , где ρ – плотность вещества в объёме dV, формулу (7) можно записать в виде

.

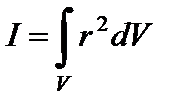(8)

Если тело однородно, т.е. его плотность ρ одинакова по всему объёму, то

.

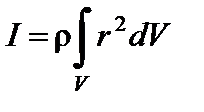(9)

Момент инерции относительно оси вращения характеризует инертность тела при вращении вокруг этой оси, т.е. является величиной, аналогичной массе тела, которая является мерой инертности тела при его поступательном движении.

Используя формулу (9), можно рассчитать моменты инерции однородных тел правильной геометрической формы.

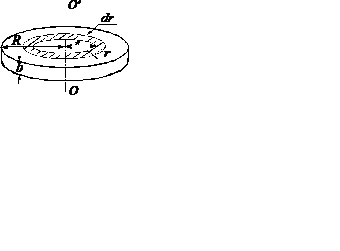
Рис. 3.

Сплошной однородный диск (цилиндр)

В качестве примера рассчитаем момент инерции сплошного однородного диска (цилиндра) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр масс (рис 3). Разобьём диск на кольцевые слои толщиной dr. Обьём такого слоя равен dV = b·2πr·dr, где b – толщина диска. Подставим выражение для dV в уравнение 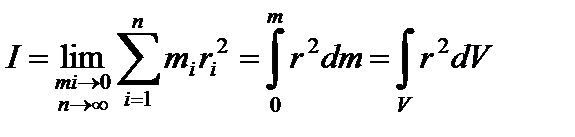и вынесем постоянные за знак интеграла: .

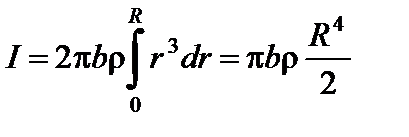Учитывая, что произведение плотности диска ρ на его объём πR²b равно массе диска, получим:

.

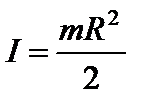(10)

Без расчёта приведём формулы момента инерции тонкого стержня длиной l относительно оси, перпендикулярной к стержню и проходящей через его середину (рис. 4)

,

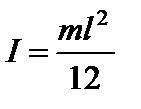(11)

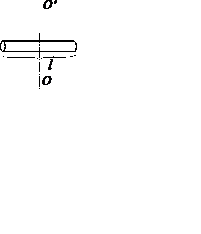
Рис. 4.

Тонкий стержень длиной l

и момента инерции шара относительно оси, проходящей через его центр масс (рис. 5):

.

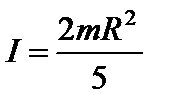(12)

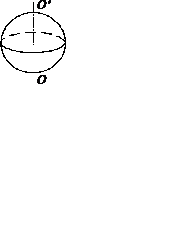
Рис. 5.

Однородный шар

Теоретический расчёт моментов инерции тел произвольной формы сложен, поэтому их определяют опытным путём.

Если для какого-либо тела известен его момент инерции I₀ относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, может быть найден по теореме Штейнера. Момент инерции твёрдого тела относительно произвольной оси (I)равен сумме моментов инерции этого тела относительно оси, параллельной данной и проходящей через центр инерции I₀ и произведения массы тела на квадрат расстояния между осями:

I = I0 + md2,

(13)

где m – масса тела; d – расстояние от центра масс до оси вращения.

Векторное произведение радиуса-вектора 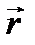на её импульс 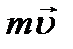называется моментом импульса 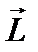этой материальной точки относительно точки О:

.

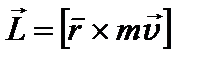(14)

Моментом импульса тела относительно точки C называется векторная сумма моментов импульса 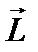всех частиц тела относительно этой точки:

.

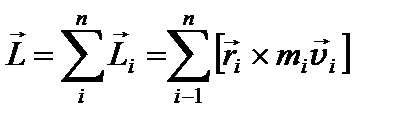(15)

Если материальная точка вращается по окружности радиуса r (рис. 6), то момент импульса относительно оси вращения ОО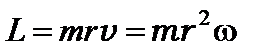^¢ ,так как 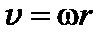, где – w угловая скорость.

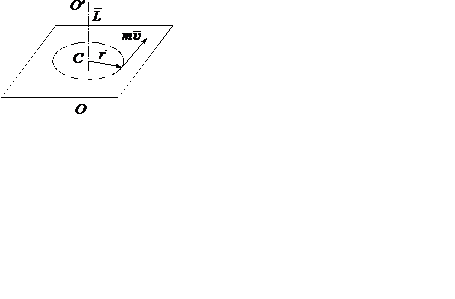
Рис. 6.

Вращение материальной точка по окружности радиуса r

Если вокруг оси ОО′ вращается система материальных точек с одной и той же угловой скоростью w, то .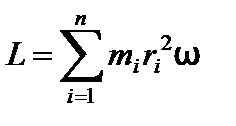

Величину w, как одинаковую для всех материальных точек, можно вынести из-под знака суммы. Тогда получится

L=Iw,

(16)

где 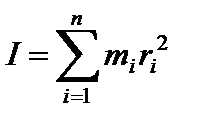- момент инерции тела относительно оси вращения.

Основной закон динамики вращательного движения тела имеет вид

,

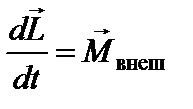(17)

где 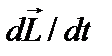- производная по времени от момента импульса тела относительно произвольного неподвижного начала, 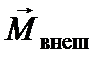- геометрическая сумма моментов всех приложенных к телу внешних сил относительно того же начала.

Основное уравнение динамики вращательного движения (17) аналогично основному уравнению динамики поступательного движения 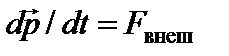и поэтому уравнение (17) называют также вторым законом Ньютона для вращательного движения.

С учётом (16) уравнение (17) можно представить в виде

.

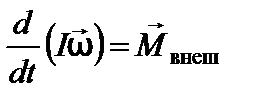(18)

Если ось неподвижна (I=const), то уравнение (18) можно записать так:
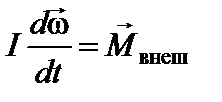, или

,

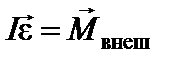(19)

где ε – угловое ускорение.

Сравнивая формулы 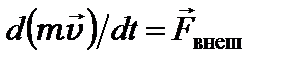и 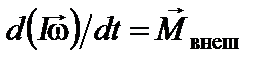убеждаемся, что эти формулы аналогичны. Аналогом силы 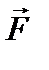, входящей в уравнение динамики поступательного движения, является момент силы в случае вращательного движения твёрдого тела, линейной скорости поступательного движения – угловая скорость вращающегося тела, массы – момент инерции тела.