Элементы квантовой электроники

Коэффициенты Эйнштейна для индуцированных переходов в двухуровневой системе. Принцип работы квантового генератора. Твердотельные и газоразрядные лазеры. Радиоспектроскопия. Первый мазер. Метод трех уровней. Открытый резонатор. Первые лазеры.

Элементы квантовой статистики

Статистическое описание квантовой системы, различие между квантовомеханической и статистической вероятностями. Теорема Нернста и ее следствия. Симметрия волновой функции многих одинаковых частиц. Квантовые идеальные газы; распределения Бозе и Ферми.

Конденсированное состояние

Строение кристаллов. Исследование кристаллических структур методами рентгено-, электроно-, нейтронографии. Точечные дефекты в кристаллах: вакансии, примеси внедрения, примеси замещения. Краевые и винтовые дислокации. Дислокация и пластичность.

Акустические и оптические колебания кристаллической решетки. Экспериментальное исследование колебательного спектра: звук, поглощение инфракрасного излучения в ионных кристаллах, комбинационное рассеяние, неупругое рассеяние нейтронов.

Понятие о фононах. Теплоемкость кристаллов при низких и высоких температурах. Решеточная теплопроводность. О квазиимпульсе фонона. Процессы переброса. Размерный эффект в теплопроводности кристаллов. Эффект Мессбауэра и его применение.

Электропроводность металлов. Носители тока в металлах. Недостаточность классической электронной теории. Электронный ферми-газ в металле. Носители тока как квазичастицы. Электронная теплоемкость. Элементы зонной теории кристаллов. Зонная структура энергетического спектра электронов. Уровень Ферми. Поверхность Ферми. Число электронных состояний в зоне. Заполнение зон; металлы, диэлектрики, полупроводники. Понятие дырочной проводимости. Собственные и примесные полупроводники.

Явление сверхпроводимости. Термодинамика сверхпроводников. Куперовское спаривание как необходимое условие сверхпроводимости. Кулоновское отталкивание и фононное притяжение. Поверхностная энергия на границе между нормальной и сверхпроводящей фазами. Сверхпроводники первого и второго рода. Роль примесей. Высокотемпературная сверхпроводимость. Захват и квантование магнитного потока. Туннельный контакт. Эффект Джозефсона и его применение.

Магнетики. Пара-, диа-, ферро- и антиферромагнетики. Теория ферромагнетизма. Обменное происхождение молекулярного поля. Доменная структура. Техническая кривая намагничивания. Теория молекулярного поля антиферромагнетиков Ферриты.

Жидкие кристаллы

Тыпы жидких кристаллов: нематики, холестирки, смектики. Примеры жидких кристаллов. Фазовые диаграммы. Упругие свойства нематиков. Поведение в электрическом и магнитном полях.

Вещество в экстремальных условиях

Вещество при сверхвысоких температурах и сверхвысоких плотностях. Металлический водород. Уравнение состояния вещества при больших плотностях. Карликовые белые звезды. Нейтронное состояние вещества. Пульсары. Вещество в сверхсильных электромагнитных полях.

СОВРЕМЕТННАЯ ФИЗИЧЕСКАЯ КАРТИНА МИРА

Вещество и поле. Атомно-молекулярное строение вещества. Атомное ядро. Кварки. Элементарные частицы, лептоны, адроны. Взаимопревращения частиц. Сильное, электромагнитное, слабое и гравитационное взаимодействия. Иерархии взаимодействий. О единых теориях материи. Физическая картина мира как философская категория.

ПРИМЕНЕНИЕ МИКРОКАЛЬКУЛЯТОРА

ПРИ РЕШЕНИИ ЗАДАЧ

Важнейшим средством совершенного научного исследования является математическое моделирование физических явлений и исследование этих моделей с помощью ЭВМ. Совершенные ЭВМ позволяют проводить сложнейшие расчеты. В некоторых областях науки, например астрофизике, проведение реальных экспериментов практически невозможно, поэтому исследователями проводится вычислительный эксперимент. ЭВМ нужны не только для проведения машинного эксперимента, но и для обработки результатов реальных экспериментов. Совершенный физический эксперимент часто дает столько информации, что обработать ее без ЭВМ практически невозможно.

Для решения любой задачи необходим алгоритм. Под алгоритмом понимают понятное и точное предписание ЭВМ совершать последовательность действий для достижения указанной цели или решения конкретной задачи. Всякий алгоритм строится в расчете на конкретного исполнителя. Таким исполнителем для проведения инженерных и студенческих расчетов различного вида заданий являются микрокалькуляторы семейства «Электроника». Это электронно-вычислительное устройство миниатюрных размеров индивидуального пользования. Оно может быть успешно использовано при решении задач, предлагаемых в контрольных работах. Выполняя вычисления с помощью микрокалькулятора, вы экономите время, освобождая его для изучения теоретических основ курса физики.

Прежде чем пользоваться микрокалькулятором, внимательно ознакомьтесь с руководством по эксплуатации:

— изучите общие сведения об устройстве;

— ознакомьтесь с правилами подготовки его к работе.

Рассмотрим решение следующих задач с применением микрокалькулятора.

1. Вычислить эффективный диаметр молекул азота, если его критическая температура 126 К, критическое давление 3,40 МПа.

Дано: Т_кр = 126 К; р_кр = 3,40 · 10⁶ Па.

Найти: d.

Решение. Азот, согласно условию задачи, должен подчиняться уравнению Ван-дер-Ваальса:

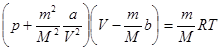
Постоянную b в уравнении Ван-дер-Ваальса с достаточной степенью точности считают равной учетверенному собственному объему 1 моль газа. В 1 моль газа находится 6,02 · 10²³ молекул (N_А = 6,02 · 10²³ моль), следовательно, объем одной молекулы равен πd³/6 = b/(4N_А), откуда 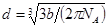. Постоянная b = RT_кр/(8p_кр), тогда

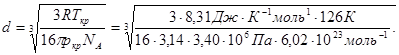
Вычисляем на калькуляторе выражение

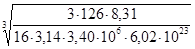
по программе

3 × 126 × 8,31 ÷ 16 ÷ 3,14 ÷ 3,40 ВП 6 ÷ 6,02 ВП 23 F 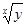3 =

Показания индикатора:3,126 – 10, т.е. 3,126 · 10^-10.

Так как данное выражение состоит только из произведения и частного, то, согласно правилам округления, его надо округлить до такого числа значащих цифр, которое имеет наименьшее точное исходное данное.

Ответ: 3,13 · 10^-10 м.

2.Определить сколько ядер в 1 г радиоактивного ⁹⁰₃₈Sr распадается в течение одного года.

Дано:m = 10^-3 кг; T = 27 лет; t = 1 год.

Найти: N.

Решение. Для определения числа атомов, содержащихся в 1 г ⁹⁰₃₈Sr, используем соотношение

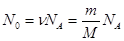, (1)

где N_А – постоянная Авогадро; ν – число молей, содержащихся в массе данного элемента; М – молярная масса изотопа. Между молярной массой изотопа и его относительной массой существует соотношение

М = 10^-3 А кг/моль. (2)

Для всякого изотопа относительная атомная масса весьма близка к его массовому числу А, т.е. для данного случая М = 10^-3 ·90 кг/моль = 9 ·10^-2 кг/моль.

Используя закон радиоактивного распада

N = N₀exp(-λt), (3)

где N₀ – начальное число нераспавшихся ядер в момент t = 0; N – число нераспавшихся ядер в момент t; λ – постоянная радиоактивного распада, определим количество распавшихся ядер ⁹⁰₃₈Sr в течение 1 года:

N’ = N₀ – N = N₀[1 – exp (-λt)]. (4)

Учитывая, что постоянная радиоактивного распада связана с периодом полураспада соотношением λ = ln2/T, получаем

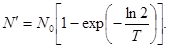(5)

Подставляя (1) с учетом (2) в выражение (5), имеем

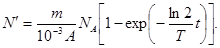(6)

Произведя вычисления по формуле (6), найдем

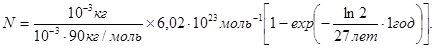
Вычислим на калькуляторе выражение

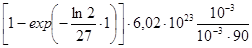
по программе

2 ln × 1 ÷ 27 = /–/ F e^x х→П 1 – П→х = × 6,02 ВП 23 × 1 ВП 3 /–/ ÷ 1 ВП 3 /–/ ÷ 90 =

Показания индикатора: 1,69532 20, т.е. 1,69532 · 10²⁰.

Ответ: 1,70 · 10²⁰.