РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА Основные С ТОКОМ В МАГНИТНОМ ПОЛЕ. ФОРМУЛЫ ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ИНДУКТИВНОСТЬ

1. Работа перемещения замкнутого контура с током в магнитном поле А= I∆Ф,

где ∆Ф – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре.

2. Основной закон электромагнитной индукции (закон Фарадея–Максвелла)

еi= −N dt= − dt,

где ei– электродвижущая сила индукции; N – число витков контура; y – потокосцепление. Частные случаи применения основного закона электромагнитной индукции:

разность потенциалов U на концах проводника длиной l, движущегося со скоростью v в однородном магнитном поле,

U = Blv×sin a,

где a – угол между направлениями векторов скорости v и магнитной индукции В; электродвижущая сила

индукции i, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью w в однородном магнитном поле с индукцией В

ei= BNSw×sinwt,

где wt – мгновенное значение угла между вектором rи вектором нормали rк плоскости рамки. 3. Количество электричества Q, протекающего в контуре,

Q = ∆y,

где R – сопротивление контура; ∆y – изменение потокосцепления.

4. Электродвижущая сила самоиндукции i, возникающая в замкнутом контуре при изменении силы тока в нем,

ei= −L dI, или еi = −L ∆t,

где L – индуктивность контура.

5. Потокосцепление контура

y = L×I,

где L – индуктивность контура.

6. Индуктивность соленоида (тороида):

r

e

В

n

R

e

dt

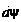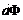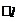где V – объем соленоида.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

L =µ0µn2V,

Основные

ФОРМУЛЫ

1. Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L , опреде-ляется формулой

W = 1LI2,

где I – сила тока в контуре.

2. Объемная (пространственная) плотность энергии однородного магнитного поля длинного соленои-да

w = µ02 2= 2В0µ= B×H.

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ Основные И ВОЛНЫ ФОРМУЛЫ

1. Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

T = 2p LC,

где L – индуктивность контура; С – его электроемкость.

2. Связь длины электромагнитной волны с периодом Т и частотой n колебаний

l = сТ или l = с,

где с – скорость электромагнитных волн в вакууме (с = 3×108м/с). 3. Скорость электромагнитных волн в среде

µ

n

,

В

,

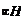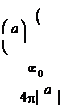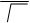
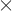
V =

с

eµ

где e – диэлектрическая проницаемость; µ – магнитная проницаемость среды.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ЗАДАЧА 1. Определить индукцию магнитного поля в центре проволочной квадратной рамки со сто-роной а, если в рамке течет ток I.

Дано: Решение

а,I a2 =180o− a1

В = ? a2

J

a1

a

r

B

В = 4В1

1 = µ0 ×I× cosa1 −cosa2 ) 4pç2ø

B= 4× æ Iö ×2cosa1

è 2ø

ЗАДАЧА 2. По двум бесконечно длинным прямым параллельным проводникам, расстояние между ко-торыми d, текут токи I1 и I2 в противоположных направлениях. Определите магнитную индукцию В в точке А, удаленной на расстоянии r1от первого и r2от второго проводника.

Дано: Решение

I1, I2, d,

B2

в b = 180º – a B

a r2

r

r

r

=

B

r

+В

В

)

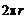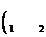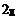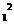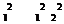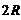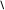
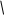
r1

B

I2

I1 d r1, r2

B = ?

µ0I11 2pr

B2=µ0I2. B=B+B2.2

Результирующую магнитную индукцию найдем по теореме косинусов: В= 12 22+2В2 cosb, cosa = 12+r2−d2,

1 2

B=µ0× I12+I22−I1I2×r2+r2−d2.

r r r r

ЗАДАЧА 3. Напряженность Н магнитного поля в центре кругового витка с магнитным моментом pm=1,5A×м2равна 150 А/м. Определите: 1) радиус витка; 2) силу тока в витке.

Дано: Решение

Н = 150 А/м pm=1,5 А·м2

H = I; pm= I ×S = IpR2= H ×Ip2R3,

R = ?

I = ?

откуда R = 3H×I×2p=11,7×10−2м,

I = H ×2R =35,1 А.

ЗАДАЧА 4. Бесконечно длинный провод образует круговую петлю, касательную к проводу. По прово-ду идет ток силой I. Найти радиус петли, если известно, что напряженность магнитного поля в центре пет-ли равна Н.

Дано: Решение

H, I I

R = ?

R

I

По принципу суперпозиции полей:

H = H1+ H2= I+ 2I = Iæ1+ 1ö= I×0,66 A/м ,

откуда R = I×0,66.

ЗАДАЧА 5. Между полюсами магнита на двух тонких нитях подвешен горизонтально линейный про-водник весом Р = 0,1 Н и длиной l = 0,2 м. Напряженность однородного магнитного поля Н = 2×105А/м и направлена вертикально. Весь проводник находится в магнитном поле. На какой угол a от вертикали от-клонятся нити, поддерживающие проводник, если по нему пропустить ток I = 2 A? Весом нитей пренеб-речь.

Дано: Решение

(

)

pR

R

H

r

r

T

A

Р

Р

r

r

В

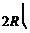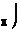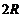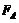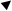
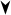
Р = 0,1 Н l = 0,2 м

Н = 2×105А/м

I= 2 A FA

a = ?

T a a

I

Сила Ампера FA= B× I ×l

B p

Условие равновесия проводника:

r+FA+P=0,т. е.

T sina = F , T cosa = Р,

или

tg×a = Р= BI ×l = µ0HI ×l »1, тогда

a = 45o.

ЗАДАЧА 6. a-частица, момент импульса которой L =1,33×10−22кг ×м2/с, влетает в однородное маг-

нитное поле, перпендикулярное скорости ее движения. Индукция магнитного поля равна 2,5×10−2Тл. Най-ти кинетическую энергию a-частицы.

Дано: Решение

L =1,33×10−22кг×м2/с B = 2,5×10−2Тл

B ^ v

q v

Fл

q =3,2×10−19Кл rm = 6,64×10−27кг

ЕК= ?

На заряд, движущийся в магнитном поле, действует сила Лоренца, которая выполняет роль центрост-ремительной силы:

Bqv = m×v2,

откуда

R= m×v.

L = mvR = mv× Bq= Bq×mv2,

mv2 = L×B×q,

следовательно,

mv2 L×B×q 1,33×10−22×2,5×10−2×3,2×10−19k 2 m×2 6,64×10−27×2

=0,8×10−16Дж =500эВ.

ЗАДАЧА 7. Тонкий медный провод массой m = 1 г согнут в виде квадрата, и концы его замкнуты. Квад-рат помещен в однородное магнитное поле (В = 0,1 Тл) так, что плоскость его перпендикулярна линиям ин-дукции поля. Определить количество электричества, если квадрат, потянув за противоположные вершины, вытянуть в линию.

R

Bq

mv

m

m

= =

=

=

E

dt

dt

dq

Ф

,

R

R

m

S

S

S

Bm

r×

a

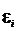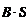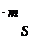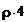Дано:

m =10−3 кг В = 0,1Тл,

r =8600кг/м3

r =1,7×10−8 Ом×м

q = ?

Решение

Согласно закону Фарадея для электро-магнитной индукции:

ei= − dФ.

По закону Ома для полной цепи I = R, где I = dq,

dtR = − dt, dq = − R× dt. (1)

Выражение (1) проинтегрируем:

q = − 1 ×( 2 −Ф1)

где Ф2=0, Ф = В×S.

q = B×S, m = r ×V = r ×4a×S ,

где S1 – площадь поперечного сечения проводника; а – сторона квадрата; r1 – плотность меди; V – объем проводника.

a = r×41. Сопротивление

R = r×l= r×4a,

1 1

где r – удельное сопротивление.

q = B×a4×S= B×a×S= r×4×r1×4× 1= 16×r×r = 42,7×10−3Кл.

ЗАДАЧА 8. В однородное магнитное поле напряженностью Н помещена квадратная рамка со стороной а. Плоскость рамки составляет с направлением магнитного поля угол a. Определить магнитный поток, пронизывающий рамку.

Дано: Решение

Н, а, a r– нормаль к рамке. H Магнитный поток