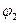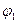Пьезоэлектрический эффект

Кристаллы, не имеющие центра симметрии (в том числе все сегнетоэлектрики) при де­формации поляризуются. Это явление называют прямым епье-зоэлектрическим эффектом. Величина поляризованное™ про­порциональна деформации и при изменении знака деформации знак поляризации меняется на обратный. Важнейшие пьезо­электрические кристаллы - кварц, сегнетова соль, метатитанат бария и др. Причиной пьезоэлектрического эффекта является возникающий при деформации сдвиг подрешеток кристалла друг относительно друга, вызывающий появление электриче-

ского момента.

Наряду с прямым пьезоэффектом у пьезоэлектриков на­блюдается обратный эффект, заключающийся в том, что поля­ризация кристалла под действием электрического поля сопро­вождается механической деформацией кристалла.

Прямой и обратный пьезоэффекты используются для воз­буждения ультразвука, стабилизации частоты генераторовэлектрических колебаний, преобразования механической энер­гии в энергию электрического поля и др.

Обратный пьезоэлектрический эффект следует отличать от электрострикции, которая имеет место во всех диэлектриках. Электрострикция также заключается в деформации диэлектри­ка под действием электрического поля, но при этом деформа­ция квадратично зависит от поля и при изменении направления поля знака не меняет.

Сегнетоэлектрики

Это - кристаллические нецентросимметричные диэлектрики, обладающие в определенном промежутке температур спонтанной (самопроизвольной) поляризацией. Впервые сегнетоэлектрические свойства были обнаружены у сегнетовой соли. В настоящее время известны несколько сотен сегнетоэлектрических веществ. Физика сегнетоэлектриков по­лучила наиболее быстрое развитие после обнаружения сегнетоэлектрических свойств у метатитаната бария (ВаТЮ₃).

Характерные особенности сегнетоэлектриков:

1. Большие диэлектрические проницаемости - несколько тысяч и более.

2. Нелинейная зависимость между поляризованностью Р и напряженностью электрического поля Е (ветвь 1 на рис.92).

. При изменении поля вектор поляризованности (и век­тор электрического смещения) отстает от напряженно­сти поля, образуя график зависимости, называемый петлей диэлектрического гистерезиса. При первона­чальном включении поля поляризованность растет с Е по ветви кривой 1. Уменьшение Р происходит по ветви 2. При обращении Е в нуль поляризованность, назы­ваемая остаточной, сохраняется. Под действием обрат­ного поля Ее (оно называется коэрцитивным) поляри­зованность становится равной нулю.

По похожести свойств сегиетоэлектриков на магнитные свойства ферромагнетиков в зарубежной литературе сегнето-электрики называют ферроэлектриками. Кристаллы сегнето-электриков, как правило, распадаются на области, в пределах которых дипольные моменты параллельны друг другу. Области носят название домены. Предельная температура, до которой сохраняются сегнетоэлектрические свойства, называется тем­пературой Кюри.

Электрический ток

Если в проводнике создать электрическое поле, то носители заряда придут в упорядоченное движение: положительные – в направлении поля, отрицательные – в противоположную сторону. Упорядоченное движение зарядов называется электрическим током. Его принято характеризовать силой тока – скалярной величиной, равной заряду, переносимому носителями через рассматриваемую поверхность в единицу времени. Если за время 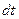переносится заряд 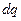, то сила тока, по определению, равна:

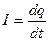. (1)

Электрический ток может быть обусловлен движением как положи-тельных, так и отрицательных носителей. Перенос отрицательного заряда в одном направлении эквивалентен переносу того же по величине положительного заряда в противоположном направлении. За направление тока принимается направление, в котором перемещаются положительные носители.

Ток, не изменяющийся со временем, называется постоянным или стационарным. Для стационарного тока характерна одинаковая сила тока в любом поперечном сечении проводника, по которому он течет.

Если в проводнике создать электрическое поле и не принять мер к его поддержанию, то от конца проводника с большим потенциалом положительные носители подойдут к концу с меньшим потенциалом, эти потенциалы выравниваются и перемещение зарядов прекратится.

Для поддержания постоянного тока необходимо заряды, подходящие к концу с меньшим потенциалом, возвращать к концу с большим потенциалом. При этом заряды должны перемещаться против действия сил электрического поля и, следовательно, осуществить такой перенос зарядов могут лишь силы неэлектрического происхождения. Такие силы получили названиесторонних сил. Всякое устройство, в котором возникают сторонние силы, называют источником тока.

Таким образом, роль источников тока заключается в возвращении электрических зарядов от участков с меньшим потенциалом к участкам цепи с большим потенциалом. Сторонние силы могут развиваться при протекании химических реакций, термодиффузии, механическом разделении заряда и т.д. Соответственно различное устройство имеют и источники тока, в которых действуют эти сторонние силы.

В лаборатории часто применяют аккумуляторы. Наибольшее распространение получили свинцовые аккумуляторы, которые называют также кислотными. В простейшем виде такой аккумулятор состоит из двух свинцовых электродов, помещенных в раствор серной кислоты. При погружении в кислоту на электродах образуется сернокислый свинец PbSO₄ и раствор насыщается той же солью. При зарядке аккумулятора на его электроде, соединенном с положительным полюсом источника, свинец окисляется в перекись PbO₂, а второй электрод (катод) превращается в чистый свинец. При разрядке аккумулятора его положительный полюс постепенно раскисляется и на нем происходит вновь образование PbSO₄, который появляется также и на отрицательном электроде.

разрядка

Суммарная реакция имеет вид:

PbO₂ + Pb + 2Н₂SO₄ 2PbSO₄ + 2Н₂O

зарядка

Для увеличения емкости аккумулятора (величины заряда, отдаваемого при разрядке) электроды отливают в виде пластин с многочисленными ячейками, куда запрессовывают окислы свинца. Вновь изготовленные аккумуляторы подвергают нескольким зарядкам и разрядкам (формовка аккумулятора).

Наряду со свинцовыми аккумуляторами применяют еще железо-никелевые или щелочные аккумуляторы, у которых один электрод из железа, второй – из никеля, а электролитом служит раствор едкого калия КОН. В заряженном состоянии анодом служит гидрат окиси никеля Ni(OH)₃, а катодом – железо. Преимуществом щелочных аккумуляторов являются их меньший вес, простота ухода.

Сторонние силы принято характеризовать работой, которую они совершают над перемещающимися зарядами. Величина, равная работе сторонних сил, отнесенной к единице положительного заряда, называется электродвижущей силой(эдс) 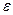, действующей в цепи или на ее участке.

Если работа сторонних сил над зарядом 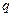равна 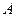, то, по определению:

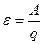. (2)

Размерность эдс совпадает с размерностью потенциала.

Кроме сторонних сил, на заряд действуют силы электростатического поля 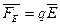, где Е - напряженность электростатического поля. Работа всех сил над переносимым по некоторому участку цепи зарядом 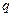складывается из работы сторонних сил (равной 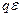, согласно (2)) и работы электростатических сил: 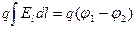. Полная работа над зарядом

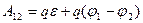. (3)

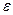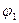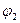Здесь – электродвижущая сила, действующая на рассматриваемом участке цепи, а и – потенциалы концов этого участка. Для замкнутой цепи работа электростатических сил равна нулю и .

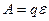Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещениии единичного положительного заряда, называется падением напряжения или просто напряжением 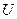на данномучастке цепи. По формуле (3)

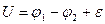. (4)

При отсутствии сторонних сил напряжение 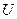совпадает с разностью потенциалов .

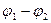Участок цепи называется однородным, если в нем не действуют сторонние силы. В таком проводнике, как установил Ом, сила тока прямо пропорциональна падению напряжения на нем:

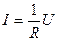. (5)

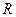называют электрическим сопротивлением проводника. Следует отметить, что линейная взаимосвязь между током и напряжением имеет место не всегда. Для ряда веществ наблюдается отступление от закона Ома. Особенно часты такие отступления для диэлектриков и полупроводников в области сильных полей. Для полупроводников отступления от закона Ома в слабых полях могут быть вызваны свойствами контактов и другими причинами.

При прохождении по проводнику тока проводник нагревается. Джоуль и независимо от него Ленц обнаружили экспериментально, что количество выделяющегося тепла пропорционально его сопротивлению, квадрату силы тока и времени:

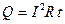. (6)

Закон этот получил название закон Джоуля-Ленца. Закон имеет простое объяснение. В однородном проводнике, к которому приложено напряжение 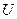, за время 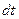через каждое его поперечное сечение проходит заряд 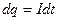. Такой заряд переносится от одного конца проводника к другому, при этом силы поля совершают работу 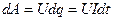. По закону Ома, 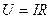, потому, интегрируя, можно получить для работы электрических сил выражение, совпадающее с выражением (6) для 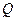. Таким образом, нагревание проводника происходит за счет работы, совершаемой силами поля над зарядами.

Закон Ома в виде (5) справедлив для однородного участка цепи, т.е. участка, в котором не действует электродвижущая сила. Чтобы получить выражение закона Ома для неоднородного участка цепи, содержащего эдс, будем исходить из закона сохранения энергии. Пусть на концах участка поддерживается разность потенциалов 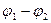. Эдс, действующую на этом участке, обозначим 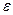. Задавшись определенным направлением (например, обозначенным на рис. 1 стрелкой), ток I и эдс 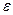нужно рассматривать как алгебраические величины. Ток будем считать положительным, если он течет в направлении, указанном стрелкой, и отрицательным – при противоположном направлении. Аналогично эдс будем считать положительной, если она действует в направлении стрелки (при этом сторонние силы совершают над положительным зарядом, перемещающимся в этом направлении, положительную работу), и отрицательной, если она действует в противоположную сторону.

		I > 0

Рис.

Если проводники, образующие участок цепи, неподвижны, единственным результатом прохождения тока будет нагревание проводников. Поэтому работа всех сил (электростатических и сторонних), совершаемая над носителями заряда, должна быть равна выделившемуся теплу. За время 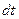по проводнику переносится заряд 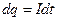. Согласно формуле (3), работа, совершаемая над этими зарядами, равна

.

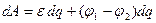За время 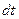выделится тепло

.

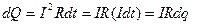Приравнивая эти два выражения, получаем:

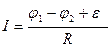. (7)

	I

R

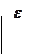Это для участка цепи:

Формула (7) выражает закон Ома для участка цепи, содержащего эдс. При 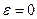она переходит в закон Ома для однородного участка. При 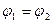получим закон Ома для замкнутой цепи:

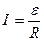. (8)

Пользуясь выражением (7), следует помнить, что под 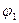надо иметь в виду потенциал точки, из которой вытекает ток, а под 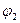– потенциал точки участка цепи, к которой ток подходит. Эдс надо считать положительной, если при переносе положительного заряда в выбранном направлении протекания тока источник тока совершает положительную работу. Иными словами, эдс положительна, если в выбранном направлении протекания тока источник включен от минуса к плюсу. Получение отрицательной величины силы тока означает, что на данном участке цепи ток течет в направлении, противоположном выбранному.

Расчет разветвленных цепей значительно упрощается, если воспользоваться правилами Кирхгофа. Этих правил два. Первое правило относится к узлам тока. Узел тока – это точка схождения трех или более проводников. Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

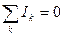. (9)

При этом приписывают токам, подходящим к узлу, один знак (например, плюс), а выходящим из узла – другой (например, минус). Первое правило Кирхгофа не является самостоятельным физическим законом. Это следствие стационарности электрических токов. В самом деле, если бы алгебраическая сумма токов не равнялась бы нулю, то в узле происходило бы накапливание зарядов. Это приводило бы к изменению потенциала узла, что, в свою очередь, приводило бы к изменению сил токов, сходящихся в узле. Уравнение (9) можно записать для каждого из N узлов разветвленной цепи, но независимыми из них являются только N – 1.

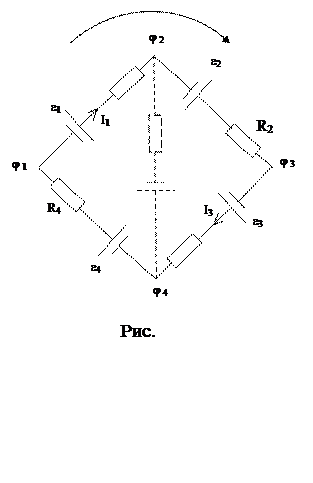
Мысленно выделим в разветвленной цепи замкнутый контур 1-2-3-4-1 (рис. 2). Зададимся направлением обхода этого контура. Делать это можно произвольно. На рис. 2 выбранное направление обхода обозначено стрелкой.

К каждому из неразветвленных участков цепи применим закон Ома для участка цепи, содержащего эдс (7):

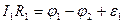
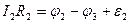
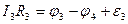
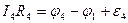
При сложении этих выражений потенциалы сокращаются, и получается уравнение:

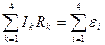. (10)

Уравнение (10) выражает второе правило Кирхгофа: алгебраическая сумма падений напряжений на сопротивлениях замкнутого контура равна алгебраической сумме эдс.

Уравнение (10) можно записать для любого замкнутого контура разветвленной цепи, но число независимых уравнений равно числу простых контуров, имеющихся в цепи, т.е. контуров, внутри которых отсутствуют разветвления цепи.

При составлении уравнений по второму правилу Кирхгофа падения напряжения считают положительными, если они создаются токами, текущими в направлении обхода контура, и отрицательными – в противном случае. Эдс положительны, если в направлении обхода контура они включены от минуса к плюсу.

Число независимых уравнений, составленных по первому и второму правилам Кирхгофа, должно быть равно числу токов, текущих в разветвленной цепи.

	R1
		R3

Рис.

Каждый источник тока характеризуется эдс 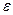и внутренним сопротивлением источника 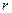. Силу тока в цепи, содержащей источник тока и нагрузочное сопротивление 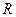(рис. 3), можно записать, используя соотношение (8):

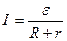. (11)

Напряжение на нагрузке, совпадающее с напряжением на зажимах эдс АВ, меньше эдс:

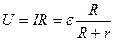. (12)

При 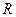→∞, → 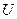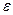напряжение на зажимах разомкнутого источника тока равно 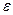. Применив формулу (3) к замкнутой цепи, получим, что для переноса вдоль цепи заряда 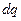источник должен совершить работу 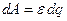, а развиваемая им мощность:

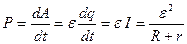. (13)

В нагрузке выделяется только часть этой мощности – полезная мощность:

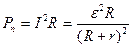. (14)

Остальная мощность расходуется в источнике тока и оказывается бесполезной. Отношение полезной мощности ко всей мощности, развиваемой источником в цепи, определяет коэффициент полезного действия (КПД) источника тока:

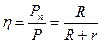. (15)

3.Магнитное взаимодействие токов