Качественное описание движения медленных ионов в газах

Повторим частично определения и выводы предыдущих лекций, но учтем при этом специфику газовой среды.

2.1.4.Рассмотрим поведение локализованного ансамбля ионов одного сорта в газе, который находится в условиях постоянной температуры и полного давления, и предположим, что из-за малой плотности числа ионов п можно пренебречь кулоновскими силами отталкивания между заряженными частицами. Как мы уже говорили ранее, процесс диффузии[8] вызывает растекание ионов по объему газа, причем их пространственное перемещение обусловлено наличием градиента концентрации ионов. Диффузионный поток частиц направлен в сторону, противоположную градиенту концентрации, а его скорость оказывается прямо пропорциональной величине последнего. Соответствующий коэффициент пропорциональности называется (скалярным) коэффициентом диффузии D. Связь плотности потока частиц J с градиентом их концентрации n устанавливается законом Фика для диффузии, который запишем в более общем виде

.

Здесь величина равняется количеству ионов, протекающих в единицу времени через единичную площадку, перпендикулярную направлению потока частиц. Знак минус учитывает то обстоятельство, что поток ионов направлен в сторону уменьшения их концентрации. Коэффициент диффузии D является суммарной характеристикой как ионов, так и частиц газа, через который они диффундируют; из уравнения следует, что D определяет меру прозрачности газа по отношению к движущимся через него частицам. Поскольку скорость диффузионного потока определяется соотношением

,

закон Фика можно также записать в виде

.

Диффузионный поток частиц поддерживается до тех пор, пока не произойдет выравнивания концентраций ионов и молекул газа. Поток такого типа следует отличать от потока частиц, вызванного неоднородностью полного давления в системе.

Если наложить теперь на газ слабое однородное электрическое поле, то возникнет установившийся поток ионов в направлении силовых линий поля, который наложится на значительно более быстрое тепловое движение ионов, приводящее к диффузии. Скорость движения центра масс ионного облака, или, что эквивалентно, средняя скорость ионов, носит название скорости дрейфа . Эта скорость прямо пропорциональна напряженности электрического поля 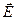при условии, что это поле поддерживается достаточно слабым. Таким образом, имеет место соотношение

,

где коэффициент К - подвижность ионов (скалярная).

Аналогично коэффициенту диффузии D подвижность ионов К представляет собой суммарную характеристику ионов и газа, в котором они распространяются.

При наличии слабого внешнего поля подвижность и коэффициент диффузии связаны между собой простой зависимостью, известной как соотношение Эйнштейна. Это соотношение является точным в предельном случае исчезающе малого электрического поля и слабой концентрации ионов. Оно устанавливает, что

;

здесь е — заряд иона,
k—постоянная Больцмана,
Т — температура газа.

Если подвижность К измеряется в обычных единицах см²/(В×с), коэффициент диффузии D — в см²/с, а температура газа T — в К, то можно записать

(при нахождении численного коэффициента в последнем уравнении использовался множитель 299,79, поскольку в СГСЭ подвижность имеет размерность 1 см², отнесенного к 1 ед. напряжения в гауссовой системе СГС и к 1 с, а 1 ед. напряжения в гауссовой системе СГС равна 299,79 В.)

2.1.5.Не удивительно, что в рассматриваемых условиях подвижность К, прямо пропорциональна коэффициенту диффузии D. Дело в том, что обе эти величины служат мерой того, насколько легко поток ионов распространяется через газ. Существенно отметить, что соотношение справедливо только в том случае, когда напряженность электрического поля настолько мала, что ионы находятся в состоянии, близком к термодинамическому равновесию с молекулами газа, т.е. когда выполнены условия так называемого «слабого» поля. При этом функция распределения ионов по скоростям оказывается очень близкой к максвелловской. Само движение ионов происходит главным образом как хаотическое тепловое движение за счет тепловой энергии газа, на которое накладывается медленный дрейф в направлении приложенного поля.

Скорость дрейфа ионов, определяемая уравнением достигает постоянного стационарного значения в том случае, когда ускорение ионов в направлении электрического поля, набираемое в промежутках времени между соударениями ионов с молекулами газа, уравновешивается торможением в процессе столкновении. Поскольку масса иона обычно сравнима с массой молекул в нормальных условиях требуется лишь небольшое число соударений иона с частицами газа, чтобы установилось это стационарное состояние после включения внешнего поля.

Если увеличить теперь напряженность электрического поля до уровня, при котором средняя энергия ионов значительно превышает тепловую энергию молекул газа, то возникнет ряд более сложных явлений. Тепловая энергия газа становится мало существенной, однако электрическое поле вызывает появление двух значительных компонент движения ионов: направленного движения вдоль силовых линий поля и хаотического движения, которое поддерживается за счет энергии поля, но из-за столкновений ионов с молекулами принимает беспорядочную форму.

В общем случае подвижность ионов К, определенная согласно уравнению , не является более постоянной величиной, а зависит обычно от величины отношения напряженности электрического поля к плотности числа молекул газа, т.е. от параметра E/N. Этот параметр определяет избыток средней энергии ионов, приобретаемый ими от поля в процессе стационарного дрейфа, по сравнению с энергией теплового движения. Кроме того, распределение ионов по энергии становится существенно немаксвелловским и не может быть точно рассчитано в рамках существующих теорий. Далее, диффузия ионов происходит также в направлении, перпендикулярном силовым линиям поля, со скоростью, отличной от скорости дрейфа ионов в направлении поля; поэтому коэффициент диффузии становится тензорной, а не скалярной величиной. Тензорный коэффициент диффузии имеет вид

;

здесь D_T — (скалярный) коэффициент поперечной диффузии ионов, который описывает скорость диффузии в направлении, перпендикулярном полю ,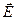
d_l—(скалярный) коэффициент продольной диффузии, характеризующий процесс диффузии ионов в направлении поля.

В описываемых здесь случаях «промежуточного» и «сильного»[9] полей соотношение Эйнштейна больше не имеет места.

Параметры E/N и E/p

Здесь мы попытаемся обосновать высказанное выше утверждение, согласно которому параметр E/N определяет среднюю энергию ионов, получаемую ими от электрического поля, или "полевую энергию". В электрическом поле на ион с зарядом е действует сила еЕ, которая сообщает ему результирующее ускорение еЕ/т, где т — масса иона. Далее мы воспользуемся грубой моделью, предполагая, что при столкновении с молекулой газа нон теряет в среднем всю ту энергию, которую он получил от поля до столкновения на длине свободного пробега. Тогда если τ — есть среднее время между последовательными столкновениями, или, проще, среднее время свободного пробега иона, то скорость иона перед столкновением равна еЕτ/т. Поскольку τ ~ 1/N, средняя энергия, получаемая ионом от поля за время между столкновениями, пропорциональна (E/N)². Точные расчеты также показывают, что параметр E/N характеризует энергию ионов в электрическом поле.

Хотя параметр E/N имеет более фундаментальное значение, до самого последнего времени большинство экспериментаторов докладывало результаты своих работ, связывая их с параметром Е/р, где р — давление газа, или с параметром Е/р₀ , где р₀ — «приведенное давление», нормированное к температуре 0°С. Величина приведенного давления определяется соотношением

;

здесь Т — абсолютная температура, при которой проводится измерение.

Такое представление результатов не было вполне удовлетворительным, поскольку символ р₀ используется также для обозначения давления, нормированного к температурам, отличным от 0°С. Однако при использовании параметра E/N сравнение разных экспериментальных результатов, перестает быть неоднозначным. Соответствующие формулы преобразования имеют вид

,

или

;

здесь E/N измеряется в единицах 10^-17 В×см²,
Т — в К, а Е/р (или Е/р₀) — в единицах В/(см×мм рт. ст.).

Хаксли, Кромптон и Элфорд (1966 г.) предложили ввести новую единицу измерения параметра E/N — «таунсенд», или сокращенно Тд, приняв, что 1 Тд == 10^-17 В×см²; с тех пор новая единица измерения широко используется. Мы будем пользоваться как параметром E/N,так и параметром Е/р.

Энергия поля пренебрежимо мала по сравнению с тепловой энергией газа, если выполняется неравенство

,

где М и m — массы молекулы и иона соответственно,
еЕλ — энергия, получаемая ионом от электрического поля на средней длине свободного пробега λ при движении его вдоль силовых линий поля.

В неравенство включен множитель, зависящий от масс сталкивающихся партнеров; в случае слабого поля и существенно различных масс иона и молекулы этот множитель учитывает то обстоятельство, что потери энергии ионом за одно столкновение значительно больше средней энергии, приобретаемой им от поля в промежутке между столкновениями. Используя уравнение состояния идеального газа р = NkT и соотношение К = 1/Ns (где N — плотность числа молекул газа, s — сечение рассеяния иона на молекуле), неравенство можно переписать в виде (М/т+m/M)eE << pσ. Рассматривая движение однозарядного иона в исходном газе и принимая физически разумное значение сечения рассеяния иона на молекуле σ = 5×10^-15 см², из равенства находим, что энергия поля значительно меньше тепловой, если

Когда этот критерий выполнен, мы будем говорить, что электрическое поле "слабое", в случае выполнения обратного неравенства будем называть поле "сильным".

Из сказанного выше можно сделать вывод, что подвижность ионов K остается постоянной величиной, не зависящей от параметра E/p при условии, что , и, следовательно, энергия ионов близка к тепловой энергии газа. На самом деле, как предсказывает теория, K является постоянной также при более высоких энергиях ионов, если частота столкновений ионов не зависит от их энергии. Однако обычно подвижность ионов начинает зависеть от параметра E/p уже вблизи верхней границы определения слабого поля. При этих условиях понятие подвижности ионов теряет ряд своих достоинств, но феноменологическое определение подвижности как отношения v_d к E полезно при сравнении экспериментальных данных и будет использоваться ниже.