Связь между линейными и угловыми величинами

Найдем скорость υ произвольной точки N тела.

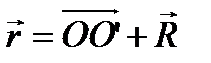Радиус-вектор точки N равен:

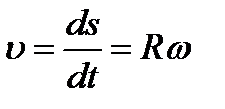
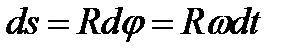Перемещаясь по дуге окружности точка N проходит путь:

Модуль скорости точки N:

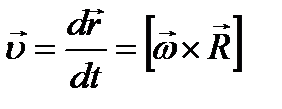Учитывая, векторы R и ω взаимно перпендикулярны и вектор скорости υ точки N направлен перпендикулярно обоим этим векторам, можем написать:

Так как векторы и коллинеарные, тогда формулу можно переписать в виде:

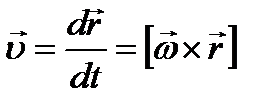
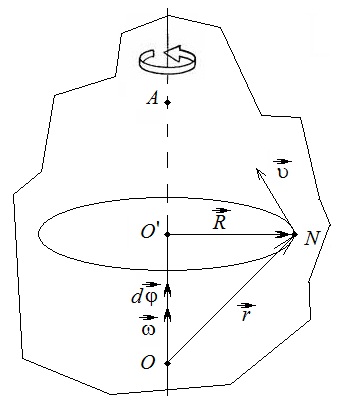
В отличие от угловой скорости тела ω скорость υ часто называют линейной скоростью точки N тела. Вектор υ направлен по правилу правого винта.

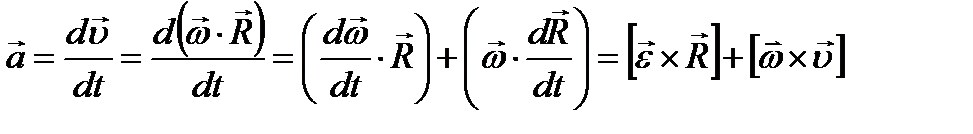Найдем ускорение точки N тела вращающегося вокруг неподвижной оси.

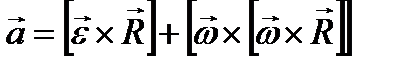
Или

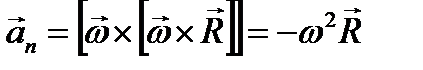
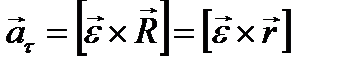Первый член в правой части этой формулы представляет собой касательное (тангенциальное) ускорение а_τ точки N:

второй – нормальное ускорение а_n точки N:

Минус в последней формуле стоит потому, что векторы а_n и R имеют противоположные направления.

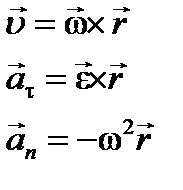В более общем виде эти выражения можно записать в векторном виде:

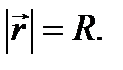
здесь - радиус-вектор м.т., проведенный из центра окружности. Его модуль равен радиусу вращения:

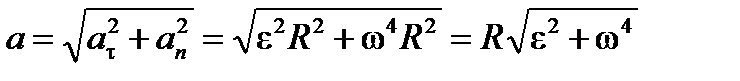Выразим полное ускорение точки через угловые величины.

название	Равномерное движение	Равнопеременное движение	Неравномерное движение
Поступательное движение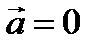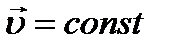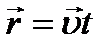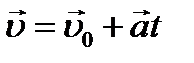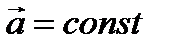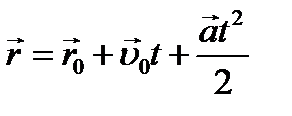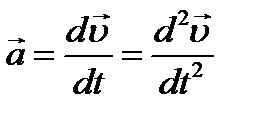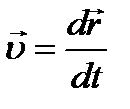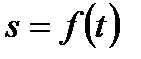
Вращательное движение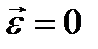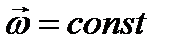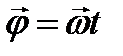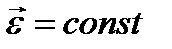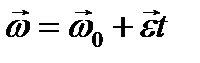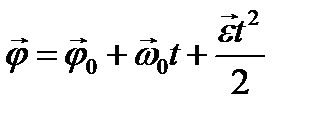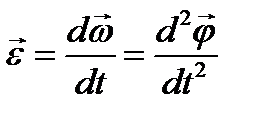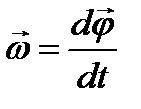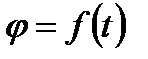

4.Прямолинейное равномерное движение. Прямолинейное равнопеременное движение.

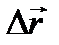Прямолинейное движение – это механическое движение, при котором вектор перемещение не меняется по направлению и по величине длине пути пройденного телом.

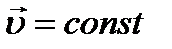Равномерным движениемназывается движение, при котором за любые равные промежутки времени точка проходит одинаковые расстояния, при этом ее вектор скорости не изменяется по величинеи он не меняет своего направления.

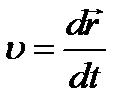
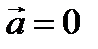Скорость постоянная, т. е.

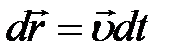
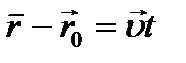
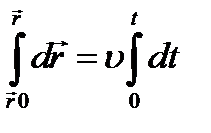Последнюю формулу проинтегрируем:

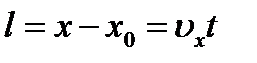
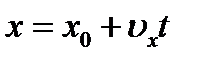
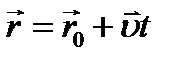Получим уравнение равномерного движения:

Равномерное прямолинейное движение

График скорости

График движения

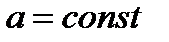Равнопеременным движениемназывают такое движение по траектории любой формы, при котором касательное ускорение является величиной постоянной

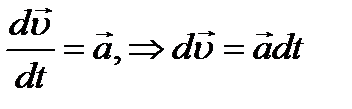Получимуравнение для равнопеременного движенияи формулу для мгновенной скорости.

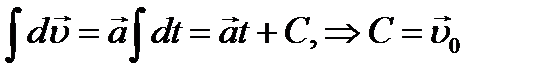Получим формулу скорости. Воспользуемся определением ускорения:

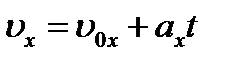
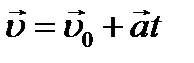Последнюю формулу проинтегрируем:

Проекция на ось ОХ имеет вид:

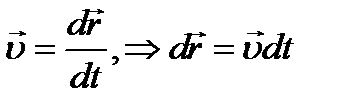Получим уравнение равнопеременного движения. Воспользуемся определением скорости:

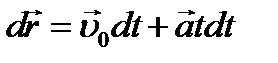
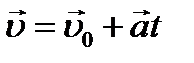
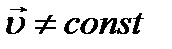Так как то с учетом получим:

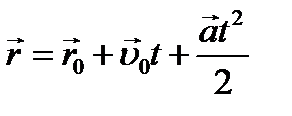
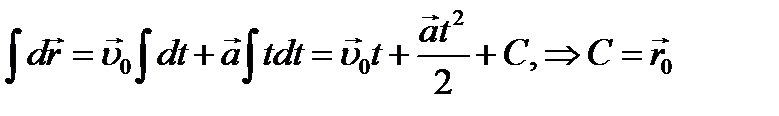Последнюю формулу проинтегрируем:

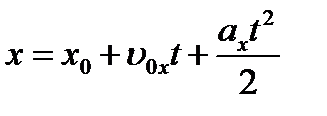
Проекция на ось ОХ имеет вид:

Равнопеременное прямолинейное движение.

График скорости.

График движения.

График ускорения.

5.Законы Ньютона.

Инерциальные системы отсчета. Сила, масса и импульс тела.
Первый закон Ньютона.

Динамика изучает механическое воздействие тел с учетом вызвавших его причин.

Динамику интересуют силы, действующие на тела.

Сила –ВФВ,характеризующаямеханическое воздействие тел и полей.

О действии сил можно судить по двум признакам:

1)Появление ускорение (динамическое действие);

2)Деформация тел (статическое действие).

Принцип суперпозиции для сил:

Если на тело действуют несколько сил, то силы действуют независимо друг от друга, и результат их действия складывается по правилам действия над векторами.

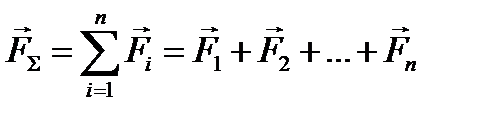Равнодействующая (результирующая) сила– это сила, оказывающая на тело такое же действие, что и данные силы вместе:

Инерциальная система отсчета (ИСО) – это система отсчета, связанная со свободным невращающимся телом.

Свободным называется тело, не взаимодействующее с другими телами.