Теория Дебая для полярных жидкостей
В полярных жидкостях поле, действующее на молекулу, существенно отличается от поля, вычисленного Лорентцем [см. ]. Поле Елв формуле представляет собой усредненное по времени поле, действующее на молекулу. При усреднении поле Е2 от молекул, заключенных в сфере радиуса R, обращается в нуль. В любой момент времени поле Е2 отлично от нуля и может иметь произвольное направление, отличное от направления среднего макроскопического поля. Величина поля E2 имеет порядок 107 в/см. Действительно, в жидкостях молекулы находятся на расстояниях примерно 2 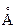 друг от друга. Если дипольные моменты молекул μ = 1 д, т. е. 10-18 CGSE единиц, то на расстоянии 2
друг от друга. Если дипольные моменты молекул μ = 1 д, т. е. 10-18 CGSE единиц, то на расстоянии 2 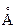 они создают поле
они создают поле
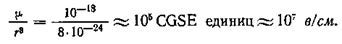
Таким образом, любая молекула находится в поле соседних молекул, достигающем 107 в/см. Направление поля, создаваемого соседними молекулами, изменяется вместе с изменением ориентации молекул, и среднее по времени значение проекции этого поля на любое перпендикулярное среднему макроскопическому полю направление равно нулю. Сильные поля соседних молекул мешают молекуле ориентироваться вдоль направления среднего макроскопического поля, так что в дипольных диэлектриках нужно учитывать поле, создаваемое соседними молекулами. Отсюда следует, что формулу Клаузиуса—Мосотти
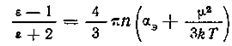 ,
,
основанную на предположении, что Е2 равно нулю, нельзя применять для вычисления ε полярных жидкостей. Первоначально Дебай считал, что дипольные молекулы жидкости могут свободно вращаться и на молекулы действует только поле Лорентца [см. ].
С понижением температуры дипольная поляризуемость молекул 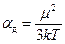 возрастает, так что правая часть формулы может стать равной единице или даже больше единицы. При этом уравнение формально удовлетворяется, если при понижении температуры диэлектрическая проницаемость стремится к бесконечности и затем становится отрицательной.
возрастает, так что правая часть формулы может стать равной единице или даже больше единицы. При этом уравнение формально удовлетворяется, если при понижении температуры диэлектрическая проницаемость стремится к бесконечности и затем становится отрицательной.
Опыт показывает, что при понижении температуры диэлектрическая проницаемость дипольных жидкостей увеличивается, оставаясь положительной и ограниченной по величине. Следовательно, в случае полярных жидкостей формула Клаузиуса— Мосотти находится в противоречии с экспериментом. Кроме того, подставляя в значение 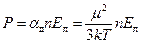 , Дебай пришел к выражению для поляризации
, Дебай пришел к выражению для поляризации
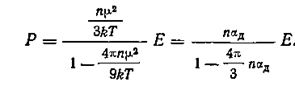 .
.
При уменьшении температуры член 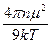 может стать равным единице и знаменатель обратится в нуль. Это приведет к тому, что коэффициент при Е в выражении для поляризации становится равным бесконечности и поляризация Р может иметь конечные значения при поле Е, равном нулю.
может стать равным единице и знаменатель обратится в нуль. Это приведет к тому, что коэффициент при Е в выражении для поляризации становится равным бесконечности и поляризация Р может иметь конечные значения при поле Е, равном нулю.
Таким образом, в полярных жидкостях, согласно первоначальной теории Дебая (так называемой старой теории Дебая) при низких температурах поляризация может возникнуть и в отсутствие электрического поля, самопроизвольно, т. е. спонтанно. Однако опытами спонтанная поляризация в дипольных жидкостях не обнаруживается. Этот неправильный вывод старой теории Дебая относительно спонтанной поляризации в полярных жидкостях называется поляризационной « 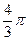 -катастрофой». Температура, при которой знаменатель в выражении для поляризации обращается в нуль и при которой должна была бы возникнуть спонтанная поляризация, называется температурой Кюри.
-катастрофой». Температура, при которой знаменатель в выражении для поляризации обращается в нуль и при которой должна была бы возникнуть спонтанная поляризация, называется температурой Кюри.
Считая, что причиной неудовлетворительности такой теории является лежащее в ее основе неправильное представление о свободном вращении дипольных молекул, Дебай создал новую теорию, в которой предполагается, что, кроме поля Лорентца ЕЛ,на молекулу со стороны соседних молекул действует большое по величине поле F, так что молекула находится в суммарном поле F' (Рис. 6‑9). Направление поля F может быть произвольным. В отсутствие внешнего электрического поля все направления поля F равновероятны. Как показал А. И. Ансельм, направление поля F определяется ориентацией соседних молекул, которая зависит от направления среднего макроскопического поля Е. Следовательно, вероятность того, что направление поля F составляет с направлением поля Е угол 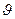 , зависит от величины Е. Однако, так как Е значительно меньше F, Дебай считал, что в электрическом поле Е все направления поля F равновероятны, т. е.
, зависит от величины Е. Однако, так как Е значительно меньше F, Дебай считал, что в электрическом поле Е все направления поля F равновероятны, т. е.
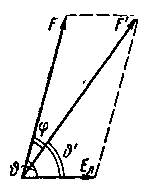 Рис. 6‑9. Электрическое поле, действующее на молекулу в жидкости Рис. 6‑9. Электрическое поле, действующее на молекулу в жидкости |
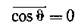 .
.
Направление поля F ', являющегося геометрической суммой полей F и ЕЛ,конечно, зависит от направления и величины Е. Направление поля F', т.е. угол 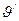 , можно определить из условия равенства вращательных моментов, действующих на равновесно ориентированный диполь со стороны полей F и ЕЛ,
, можно определить из условия равенства вращательных моментов, действующих на равновесно ориентированный диполь со стороны полей F и ЕЛ,
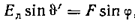 ,
,
причем направления полей Ел и Е совпадают и
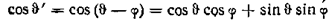 .
.
Ввиду малой величины отношения ЕЛ/F для слабых внешних полей угол 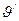 примерно равняется углу
примерно равняется углу 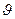 . Заменяя в уравнении
. Заменяя в уравнении 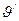 углом
углом 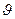 , получим
, получим
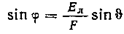 .
.
Так как угол j мал и 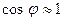 , из и найдем
, из и найдем
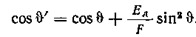
Как видно из Рис. 6‑9, напряженность поля
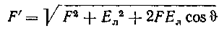 .
.
Поскольку Елмало по сравнению с F, то, извлекая корень из , получаем
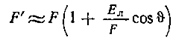 .
.
В новой теории Дебая поляризация
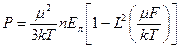
(здесь L - функция Ланжевена), старая теория Дебая приводила к следующему выражению для поляризации
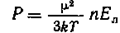 ,
,
где п — число молекул в единице объема.
Таким образом, новая теория дает для поляризации меньшую величину, чем первоначальная теория. Уменьшение поляризации объясняется тем, что в новой теории Дебая вводится поле, которое препятствует свободному вращению молекул и их ориентации вдоль направления среднего макроскопического поля.
Множитель 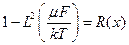 , входящий в формулу , Дебай назвал редукционным фактором. Затруднение вращения молекул приводит к кажущемуся уменьшению дипольных моментов молекул в жидкости по сравнению с дипольными моментами тех же молекул в газе
, входящий в формулу , Дебай назвал редукционным фактором. Затруднение вращения молекул приводит к кажущемуся уменьшению дипольных моментов молекул в жидкости по сравнению с дипольными моментами тех же молекул в газе
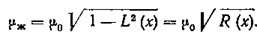
Подставив μж вместо μ, в формулу , найдем
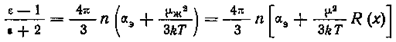 ,
,
где ε — диэлектрическая проницаемость жидкости;
п — число молекул в единице объема жидкости;
μ.ж — кажущаяся величина диэлектрического момента молекул в жидкости;
αэ — электронная поляризуемость молекул в жидкости;
μ — истинная величина момента молекул в жидкости, равная моменту молекул в газообразном состоянии: μ = μ0.
Подобно тому, как из уравнения было получено выражение , исходя из формулы , находим значение молекулярной поляризации дипольной жидкости
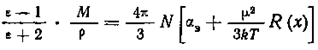 .
.
Внутреннее молекулярное поле для воды равно 2×105CGSE единиц = 6×107 в/см и редукционный фактор R (х) = 0,2. Следовательно, в сильно полярных жидкостях молекулы находятся в больших электрических полях, создаваемых соседними молекулами. Энергия молекулы в молекулярном поле w = μF в 10 раз больше, чем kT. Совершая колебания в сильном молекулярном поле F, диполи отклоняются на небольшие углы от положения равновесия.
Поляризация, обусловленная упругими поворотами диполей на небольшие углы, названа упруго-дипольной поляризацией. Упруго-дипольная поляризация устанавливается за время порядка 10-12 сек. Рассмотренная в первоначальной теории Дебая поляризация, связанная с поворотом диполей на большие углы, названа дипольно-релаксационной поляризацией. Для установления дипольно-релаксационной поляризации требуются промежутки времени от 10-10 сек и выше. Как показывают измерения, большая величина ε воды обязана дипольно-релаксационной поляризации. Упруго-дипольная поляризация в воде мала по сравнению с дипольно-релаксационной поляризацией. Упруго-дипольная поляризация важна на частотах, превосходящих 1010 гц, когда дипольно-релаксационная поляризация исчезает.
Дипольные кристаллы
Упруго-дипольная поляризация является одним из основных видов поляризации в кристаллах, содержащих связанные молекулы воды или другие полярные молекулы, которые могут совершать только упругие повороты на небольшие углы. К таким кристаллам применимы теории упруго-дипольной поляризации в жидкостях. Поэтому кратко рассмотрим явления поляризации в дипольных кристаллах.
В некоторых кристаллах, например кристаллах льда, молекулы могут вращаться, совершая повороты на большие углы. При понижении температуры число молекул, способных поворачиваться на большие углы, уменьшается. Считая, что основную роль в поляризации кристалла играют молекулы, свободно вращающиеся под действием внешнего электрического поля, и не принимая во внимание поляризацию, создаваемую упругими поворотами на небольшие углы «закрепленных» диполей, для вычисления диэлектрической проницаемости кристаллов можно применять формулу теории Дебая. Так как
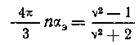 ,
,
выражение может быть представлено в виде
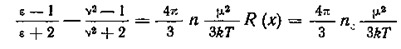 ,
,
где п — число дипольных молекул в единице объема кристалла;
nс = nR(x) — концентрация молекул, способных вращаться под действием электрического поля.
В кристаллах между способными вращаться молекулами nс и «закрепленными» молекулами (п—пс)существует динамическое равновесие: одни молекулы закрепляются, а другие освобождаются, так что при неизменной температуре число пс остается постоянным.
