Аналогии между поступательным и вращательным движениями
| Поступательное движение | Вращательное движение |
1. Линейное перемещение : 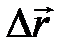 2. Линейная скорость: 2. Линейная скорость: 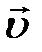 3. Линейное ускорение: 3. Линейное ускорение: 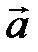 4. Масса тела: m 5. Сила: 4. Масса тела: m 5. Сила: 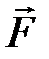 6. Работа: 6. Работа: 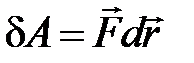 7. Мощность: 7. Мощность: 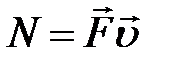 8. Кинетическая энергия: 8. Кинетическая энергия: 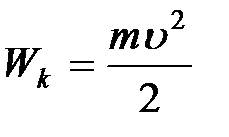 9. Импульс тела: 9. Импульс тела: 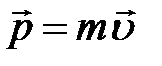 10. Второй закон Ньютона: 10. Второй закон Ньютона: 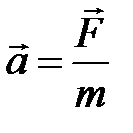 | 1. Угловое перемещение: 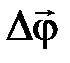 2. Угловая скорость: 2. Угловая скорость: 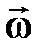 3. Угловое ускорение: 3. Угловое ускорение: 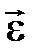 4. Момент инерции: I 5. Момент силы: 4. Момент инерции: I 5. Момент силы: 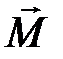 6. Работа: 6. Работа: 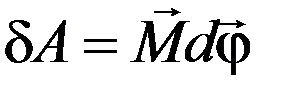 7. Мощность: 7. Мощность: 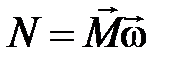 8. Кинетическая энергия: 8. Кинетическая энергия: 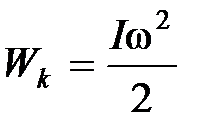 9. Момент импульса: 9. Момент импульса: 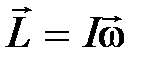 10. ОУДВД: 10. ОУДВД: 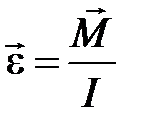 |
20. Относительность движения в классической физике.
Принцип относительности Галилея:
Все законы механики одинаковы во всех ИСО.
Преобразования Галилея позволяют сделать переход из одной ИСО в другую. В его основе лежат две аксиомы:
аксиома 1 – ход времени одинаков во всех системах отсчета.
аксиома 2 – расстояния между двумя точками, а также размеры тела в любой системе отсчета (СО) не зависят от скорости ее движения.
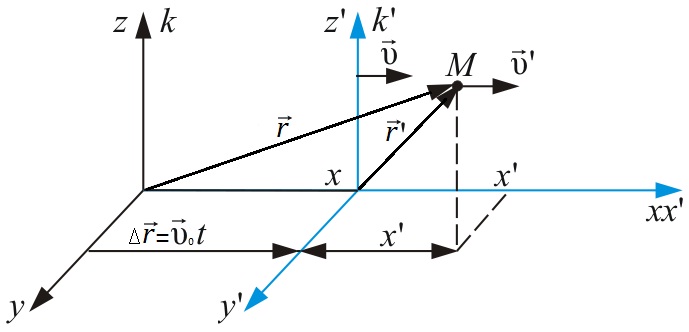
Рассмотрим две ИСО:
К – лабораторная (неподвижная) СО Oxyz
К¢ - движущаяся СО O¢x¢y¢z¢
u0 -скорость движения системы K¢ относительно системы K.
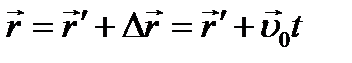 В начальный момент времени оси координат обеих СО совпадают. Пусть внутри системы K¢ находится некоторое тело M.
В начальный момент времени оси координат обеих СО совпадают. Пусть внутри системы K¢ находится некоторое тело M.
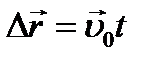
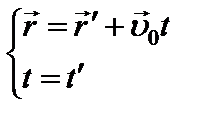
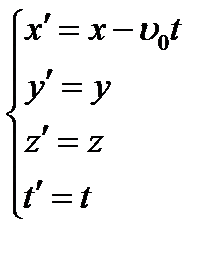
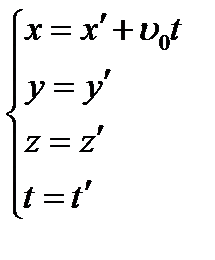 Спроектируем на координатные оси:
Спроектируем на координатные оси:
(1) Или (2)
Системы уравнений (1) и (2) называются преобразованиями Галилея.
Используя уравнения (1) и (2), можно перейти от описания движения тела в одной системе отсчета к другой системе отсчета.
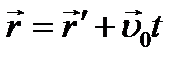 Из преобразований Галилея вытекает теорема (закон) сложения скоростей.
Из преобразований Галилея вытекает теорема (закон) сложения скоростей.
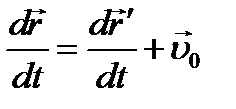 Продифференцируем по времени:
Продифференцируем по времени:
(u0 = const)
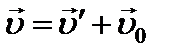 Теорема о сложении скоростей в классической механике:
Теорема о сложении скоростей в классической механике:
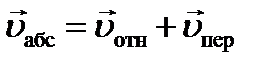 u - скорость движения точки в неподвижной ИСО К; u¢ - скорость движения точки в движущейся ИСО K¢; u0 - скорость движения системы K¢ относительно системы K.
u - скорость движения точки в неподвижной ИСО К; u¢ - скорость движения точки в движущейся ИСО K¢; u0 - скорость движения системы K¢ относительно системы K.
В теоретической механике эту теорему записывают в виде:
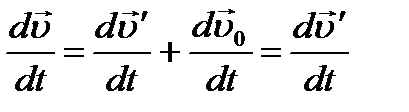 Продифференцируем полученное выражение по времени еще раз:
Продифференцируем полученное выражение по времени еще раз:
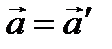
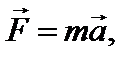
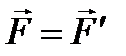
Инвариантные величины:
Величины, не изменяющиеся при переходе от одной системы отсчета к другой, т. е. не зависящие от преобразований координат, называются инвариантными величинами или инвариантами преобразований.
1)Ускорение;
2)Силы;
3)Масса;
4)Длина тела и т. д.
Принцип относительности Галилея: законы механики одинаковы во всех инерциальных системах отсчета.
Это значит, что в разных ИСО все механические процессы при одних и тех же условиях протекают одинаково.
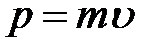 Инвариантными по отношению к преобразованиям Галилея, при переходе от одной ИСО к другой, оказываются также уравнения, вид которых не изменяется при таком переходе. Величины, входящие в эти уравнения, могут при переходе от одной СО к другой изменяться, однако формулы, выражающие связь между этими величинами, остаются неизменными.
Инвариантными по отношению к преобразованиям Галилея, при переходе от одной ИСО к другой, оказываются также уравнения, вид которых не изменяется при таком переходе. Величины, входящие в эти уравнения, могут при переходе от одной СО к другой изменяться, однако формулы, выражающие связь между этими величинами, остаются неизменными.
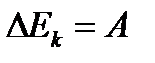
Принцип относительности Галилея: уравнения механики инвариантны по отношению к преобразованиям Галилея.
21.Постулаты СТО. Преобразования Лоренца.
Постулаты СТО.
1-ый постулат СТО (принцип относительности Эйнштейна) является обобщением классического принципа относительности с механических на любые физические явления.
Первая формулировка. Никакими физическими опытами (механическими, электрическими, оптическими) проведенными в ИСО, нельзя доказать покоится эта система или движется равномерно и прямолинейно относительно другой ИСО.
Вторая формулировка. Все процессы в природе (механические, электрические, оптические) во всех ИСО протекают одинаково.
Эйнштейн показал, что преобразования Галилея должны быть заменены более общими преобразованиями Лоренца.
Третья формулировка. уравнения выражающие законы природы, инвариантны по отношению к преобразованиям Лоренца.
2-ой постулат СТО (принцип инвариантности скорости света). Скорость света в вакууме не зависит от скоростей движения источника и приемника света, и является максимально возможной скоростью движения в природе.
c = 3,00·108 м/с
Из второго постулата следует, что скорость света в вакууме является величиной инвариантной, т. е. она одинакова для всех направлений и во всех ИСО.
Скорость света является одной из важных физических постоянных и она в вакууме является предельной.
Опыты показали, что скорость любых тел и частиц, а также скорость распространения любых сигналов и взаимодействий не может превосходить скорости света.
Механика, описывающая движения с околосветовыми скоростями, называется релятивистской механикой.
В СТО пространство и время взаимосвязаны, образуя единое четырехмерное пространство-время.
Точечное» событие характеризуется четырьмя величинами – координатами x, y и z, указывающими, где оно произошло, и временем t – когда оно произошло.
Значения этих четырех величин зависят от СО, в которой «наблюдаем» это событие.
В четырехмерном пространстве (пространство–время) возьмем прямоугольную систему координат с осями x, y, z и ct. Тогда событие можно изобразить точкой, которую называют мировой точкой.
С течением времени мировая точка изменяет свое положение в четырехмерном пространстве, описывая траекторию, которая называется мировой линией.
Если частица неподвижна в обычном пространстве, ее мировая точка перемещается параллельно оси ct.
При переходе к другой ИСО значения координат x, y, z, а также времени t изменяются и становятся равными x¢, y¢, z¢ и t¢.
Пространство:
