Электропроводность кристаллов в слабых полях

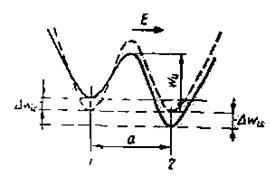Рис. 5‑4 Потенциальная кривая при наличии поля (сплошная линия) и без поля (пунктир); в потенциальных ямах 1 и 2 может находиться ион

В кристаллах частицы (атомы, ионы или молекулы), расположенные в узлах решетки, а также примесные атомы совершают тепловые колебания около положений равновесия. Когда слабо закрепленный атом (ион) получает достаточно большую тепловую энергию, он может переместиться из одного места закрепления в другое. Вероятность таких тепловых перебросов прямо пропорциональна 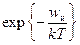, где w_и — максимум потенциальной энергии «барьера», который разделяет положения 1 и 2 (Рис. 5‑4).

Если внешние электрические силы отсутствуют (Рис. 5‑4, пунктирная кривая), наблюдается тепловая диффузия атомов во всех направлениях; вероятность нахождения атомов (ионов) в двух «потенциальных ямах» будет одинакова, и ток в кристалле окажется равным нулю.

При наложении внешнего электрического поля Е дополнительные дефекты не создаются (для этого потребовались бы поля порядка нескольких десятков МВ/см), однако глубина одной из ям (потенциальной ямы 1) 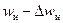станет меньше (Рис. 5‑4, сплошная кривая), чем глубина другой потенциальной ямы 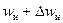и будет наблюдаться преимущественное направление движения атомов. Ввиду экспоненциальной зависимости частоты перебросов от глубины потенциальной ямы вероятность, перебросав влево и вправо станет неодинаковой. Атом (ион), находящийся в более «мелкой» потенциальной яме 1, будет иметь большую вероятность переброса (в направлении поля или в обратном направлении, в зависимости от знака носителя заряда), чем атом, находящийся в более глубокой потенциальной яме 2. В результате этого будет наблюдаться дрейф (направленный перенос) атомов (ионов), и через вещество будет протекать ток.

Концентрация дефектов по Френкелю и по Шоттки зависит от температуры экспоненциально. Поэтому можно было бы ожидать, что в области низких температур проводимость ионных диэлектриков, таких, как галоидные соединения серебра или щелочно-галоидные и щелочноземельно-галоидные кристаллы, должна быть очень незначительной. В этих кристаллах проводимость обусловлена в основном одним видом носителей тока — катионами; естественно предположить, что электропроводность таких кристаллов должна выражаться следующим образом:

,

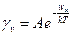где A — постоянная;
Т — абсолютная температура;
k — постоянная Больцмана;
w_и — энергия, необходимая для образования и дрейфа иона (катиона).

Если построить зависимость lgγ от величины, обратной абсолютной температуре Т, следовало бы получить наклонную прямую.

Однако на практике такая зависимость не наблюдается. Это связано с тем, что в реальных кристаллах всегда имеются дефекты из-за присутствия примесных ионов, имеющих валентность, отличную от валентности ионов основного вещества. Если в щелочно-галоидных кристаллах типа NaCl содержатся, например, двухвалентные катионные примеси, такие, как Ва, Sr, Ca, Cd и др., то они, как показывают рентгенографические исследования, входят в кристалл в качестве заместителей, т.е. примесные ионы занимают катионные узлы решетки. Так как при растворении примесей суммарный электрический заряд кристалла должен оставаться равным нулю, при замещении одного катионного узла решетки двухвалентным катионом возникнет катионная вакансия. Следовательно, при низких температурах в кристалле концентрация катионных вакансий, определяющая его удельную проводимость, будет значительно выше, чем концентрация вакансий, образовавшихся из-за тепловых флюктуации.

В реальных кристаллах может присутствовать большое число различным образом ориентированных зерен. В ряде случаев атомные плоскости двух соседних зерен кристалла могут располагаться под большим углом относительно друг друга и граничная область между ними будет сильно искажена. Вследствие этого энергия активации для перемещения слабо закрепленных атомов (ионов) на границе между зернами будет заметно меньше, чем внутри зерен. Об этом свидетельствует, в частности, тот экспериментальный факт, что удельная проводимость поликристаллических материалов больше, чем монокристаллов. Удельная проводимость (при низких температурах) кристаллов, подвергавшихся большим механическим нагрузкам, сильно возрастает.

Слабо закрепленные в решетке примеси и вакансии, возникшие из-за наличия ионов иной валентности, могут легко мигрировать во внешнем электрическом поле, так как энергия активации, необходимая для их дрейфа, сравнительно низка. Примесями и вакансиями и определяется в основном область так называемой низкотемпературной проводимости кристаллов. Энергия, которая требуется для образования дефекта, значительно больше, чем энергия, необходимая для его дрейфа. Поэтому собственные дефекты, возникающие из-за сильных тепловых флюктуации в кристалле, определяют проводимость кристалла лишь при температурах, довольно близких к температуре плавления кристалла. Для многих щелочно-галоидных кристаллов эти температуры превышают 500—600° С.

Проводимость полярных кристаллов определяется формулой

.

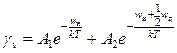Формула справедлива, когда имеет место один тип проводимости (например, в случае щелочно-галоидных кристаллов). При наличии слабо закрепленных ионов с неодинаковыми энергиями активации следует брать разные значения w_и и w_д, характерные для каждого вида иона. В этом выражении: w_и — энергия активации, необходимая для дрейфа слабо закрепленных атомов (ионов) или для дрейфа вакансий; w_д — энергия активации, необходимая для образования дефекта; Т — абсолютная температура. Коэффициенты А₁ и А₂ слабо зависят от температуры:

.

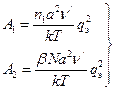Здесь n_i и N — объемные концентрации примесных ионов и число пар ионов кристалла (то и другое — в единице объема);
a—постоянная решетки;
q_э — заряд электрона;
ν'— угловая частота колебаний иона, расположенного рядом с вакансией (ν' меньше частоты нормальных колебаний в решетке ν).

Коэффициент β определяется выражением

,

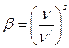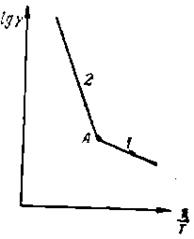Рис. 5‑5 Зависимость удельной объемной проводимости кристаллов от температуры

где s — число ионов, смежных с вакансией.

Для простой кубической решетки 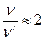, s= 6 и .

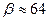В широком диапазоне температур график зависимости логарифма удельной объемной проводимости γ_v от величины, обратной абсолютной температуры Т, т. е. 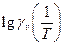, должен состоять из двух прямолинейных участков с различными значениями угла наклона к оси абсцисс (Рис. 5‑5).

При температуре выше точки излома (точка А) проводимость определяется в основном собственными дефектами. Это область 2 высокотемпературной, или собственной, проводимости. Ниже точки излома располагается область 1 низкотемпературной, или примесной (по терминологии Смекаля, «структурночувствительной») проводимости; здесь участок более пологий. Для каждого соединения граничной температурой в точке излома следует считать температуру, при которой концентрация собственных дефектов равна концентрации примесей. В отличие от низкотемпературной проводимости, определяемой в основном природой и концентрацией примесей, область 2 собственной проводимости не зависит от примесей, хорошо воспроизводится и является физической характеристикой данного соединения.

В качестве иллюстрации в Табл. 5‑1 приводятся экспериментальные значения A₁, A₂, w_и, w_д для некоторых щелочно-галоидных кристаллов.

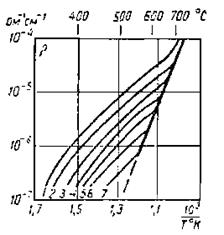
Табл. 5‑1. Значения A1, A2, wи, wд для щелочно-галоидных кристаллов. Вещество A1 wи,. ккал/моль A2 wд,. ккал/моль LiF - - 4×107 50,7 LiCI 13,6 1×106 32,6 LiBr 12,8 5×105 28,0 LiJ 0,2 8,4 2×105 21,2 NaF - — 2×106 51,9 NaCI 0,5 19,5 5×105 42,3 NaBr 0,2 18,4 2×105 38,4 NaJ 0,06 13,8 1×104 28,3 Рис. 5‑6 Влияние примеси ВаСl2 на удельное сопротивление KC1 (по Витту). Содержание BaCl2 в весовых процентах: 1 — без примеси; 2 — 1,25×10-3; 3 — 1,9×10-3; 4 — 3×10-3; 5 — 4,7×10-3; 6 — 9×10-3; 7—14×10-3

Температура, отвечающая точке излома на графике 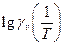, весьма резко зависит от степени чистоты и совершенства (отсутствия дефектных областей) кристаллов. В качестве иллюстрации на Рис. 5‑6 приведены данные для монокристаллов КСl с различными концентрациями примеси хлористого бария. В последние годы были развиты методы получения весьма чистых щелочно-галоидных кристаллов; излом на графике 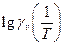для некоторых из них наблюдается при 100—150°С.

По наклону этого графика можно определить энергию активации носителей тока, а также их концентрацию. В щелочно-галоидных кристаллах концентрация равновесных дефектов в области низкотемпературной проводимости определяется выражением

,

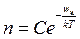где величина С, слабо зависящая от температуры, может быть определена экспериментально. Расчету равновесной концентрации посвящен ряд работ.

Концентрация дефектов п оказывает заметное влияние на электропроводность щелочно-галоидных кристаллов. Многие диэлектрики содержат кристаллизационную воду, которая начинает выделяться при нагревании до некоторой, достаточно высокой температуры. Потеря кристаллизационной воды может быть связана с резким возрастанием, удельного сопротивления.

В сравнительно редких случаях электроизоляционные материалы при нормальной температуре обладают также и электронной электропроводностью. Чисто электронный характер электропроводности обнаружен у титанатов (ВаТiO₃, BaTi₄O₉, СаТiO₃, SrТiO₃).

При значительном повышении напряженности электрического поля (в «предпробнвной» области), помимо обычной ионной электропроводимости, появляется добавочная электронная электропроводность.