Второе начало термодинамики

Второе начало термодинамики позволяет определить направление протекания процессов (определить процессы, протекание которых возможно). С этой целью вводится понятие энтропии.

Пусть dQ - количество теплоты, сообщенное телу на бесконечно малом участке изотермического процесса. Величина dQ/T называется приведенным количеством теплоты , где Т - температура теплоотдающего тела. В теории доказывается, что в замкнутой системе для любого обратимого кругового процесса 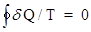, откуда следует, чтоdQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние, т.е. dQ/T = dS.

Функция состояния S, дифференциалом которой является dQ/T называется энтропией. Из 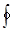dQ/T = 0 следует, что для обратимых процессов DS = 0 . Кроме того, доказывается, что для необратимого цикла DS > 0. Так что в общем случае для замкнутой системы справедливо неравенство КлаузиусаDS ³ 0.

Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии

DS = S₂ - S₁ =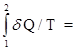

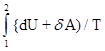
и, следовательно, энтропия определяется с точностью до аддитивной постоянной, т.е. физический смысл имеет не сама энтропия, а разность энтропии.

Используя выражения для идеального газа [dU=(m/M)C_VdT, dA=pdV=(m/M)RTdV/V], можно получить

DS = (m/M)[C_Vln(T₂/T₁) + Rln(V₂/V₁)],

т.е. изменение энтропии идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1 ® 2.

Для адиабатического процесса dQ = 0 и, следовательно S = const - т.е. адиабатический процесс протекает при постоянной энтропии (изоэнтропийный процесс). Для изотермического процесса T₁ = T₂ и, следовательно, DS = (m/M)Rln(V₂/V₁). Для изохорного процесса V₁ = V₂ и, следовательно, DS = (m/M)C_Vln(T₂/T₁).

Энтропия обладает аддитивным свойством - энтропия системы равна сумме энтропий тел, входящих в систему. Свойством аддитивности обладает также внутренняя энергия, масса, объем. Свойством аддитивности не обладают температура и давление.

В статистической физике энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W системы - это число способов, которыми может быть реализовано данное макросостояние макроскопической системы (число микросостояний, осуществляющих данное макросостояние, т.е. W ³ 1 и термодинамическая вероятность не есть вероятность в математическом смысле, т.к. последняя £1). Согласно гипотезе Больцмана S = klnW, т.е. энтропия есть логарифм числа микросостояний, с помощью которых может быть реализовано данное макросостояние (k - постоянная Больцмана).

Следовательно, энтропия является мерой неупорядоченности системы: чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия - наиболее вероятного состояния системы - число микросостояний максимально, при этом максимальна и энтропия.

Поскольку реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению энтропии (принцип возрастания энтропии): процессы в замкнутой системе идут в направлении увеличения числа микросостояний, т.е. идут от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной. Энтропия (и термодинамическая вероятность состояния) замкнутой системы может либо возрастать (для необратимых процессов), либо оставаться постоянной (для обратимых процессов).

Клаузиус так сформулировал второе начало термодинамики (закон возрастания энтропии): любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

Формулировка второго начала Кельвина: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

Таким образом, для произвольного процесса, протекающего в термодинамической системе, справедливо соотношение (второе начало термодинамики)dQ £ TdS, где Т - температура того тела, которое сообщает термодинамической системе энергию dQ в процессе бесконечно малого изменения состояния системы. Используя первое начало термодинамики dQ = dU + dA, можно записать неравенство, объединяющее первое и второе начала термодинамикиTdS ³ dU + dA.

Для обратимого процесса dA =-(dU - TdS) =-d(U - TS) - SdT = -dF - SdT, где F = U - TS называется свободной энергией, которая является разностью двух функций состояния и поэтому также является функцией состояния термодинамической системы.

Для изотермического процесса dT = 0 и, следовательно, dA =-dF, т.е. убыль свободной энергии является мерой работы, которую совершает система в обратимом изотермическом процессе.

Внутреннюю энергию системы можно записать U = F + TS, т.е. внутренняя энергия системы равна сумме свободной энергии F и связанной энергииTS. Связанная энергия - эта та часть внутренней энергии системы, которая не может быть передана в форме работы в изотермическом процессе (в этом смысле связанная энергия - это “обесцененная” энергия). Связанная энергия тем больше, чем больше энтропия системы S и поэтому энтропия системы служит мерой “обесцененности” ее энергии.

Реальные газы