Основы равновесной термодинамики

· Удельная теплоёмкость вещества: .

· Молярная теплоёмкость вещества: .

· Молярные теплоёмкости при постоянном объёме ( ) и постоянном давлении ( ):

, где - число степеней свободы, т.е.

· Связь между удельной (с) и молярной (С) теплоёмкостями:

с=С/М,

где М – молярная масса.

· Внутренняя энергия идеального газа:

.

· Работа расширения газа:

- в общем случае.

- при изобарном процессе.

- при изотермическом процессе.

- при адиабатном процессе,

где .

· Первое начало термодинамики:

,

где Q – количество теплоты, сообщённое системе, - изменение внутренней энергии системы, А – работа, совершённая системой против внешних сил.

Если над системой совершается работа ( ), то первое начало термодинамики: , причём .

· Первое начало термодинамики применительно к изопроцессам:

1) Изотермический ( ): ( );

2) Изохорный ( ): ( );

3) Изобарный ( ): ;

4) Адиабатный ( ): или .

· Уравнение Пуассона для адиабатного процесса:

, где .

· Коэффициент полезного действия цикла Карно, который состоит из двух изотерм и двух адиабат:

,

где - количество теплоты, полученное от нагревателя, - количество теплоты, переданное холодильнику, - температура нагревателя, - температура холодильника.

· Изменение энтропии при равновесном переходе из состояния 1 в состояние 2:

.

ОСНОВЫ НЕРАВНОВЕСНОЙ ТЕРМОДИНАМИКИ.

ЯВЛЕНИЯ ПЕРЕНОСА

· Средняя длина свободного пробега молекул газа

,

где - средняя арифметическая скорость, <z> - среднее число столкновений каждой молекулы с остальными за единицу времени, σ - эффективный диаметр молекулы, n - число молекул в единице объема (концентрация)

· Средняя продолжительность свободного пробега

.

· Общее число столкновений всех молекул в единице объема за единицу времени

.

· Явления переноса – возникают при отклонении газа от равновесия:

· Диффузия – возникает при градиенте плотности (концентрации) и обусловлена переносом массы.

Коэффициент диффузии

.

Масса, перенесенная за время dt при диффузии через площадку dS, расположенную перпендикулярно направлению, вдоль которого происходит диффузия

,

где - градиент плотности, знак «минус» показывает, что перенос массы происходит в направлении убывания плотности.

· Внутреннее трение (вязкость) – возникает при градиенте скорости, возникающем при движением слоёв жидкости или газа относительно друг друга и обусловлено переносом импульса молекул из слоя в слой.

Динамический коэффициент внутреннего трения (вязкости)

,

где ρ - плотность вещества.

Сила внутреннего трения, действующая на элемент поверхности слоя с площадью dS

,

где - градиент скорости, знак «минус» указывает, что импульс переносится в направлении убывания скорости.

· Теплопроводность –возникает при градиенте температуры и обусловлена переносом средней кинетической энергии молекул.

Коэффициент теплопроводности

,

где c_v - удельная теплоемкость газа в изохорном процессе.

Количество теплоты, перенесенное через поверхность dS, перпендикулярную направлению теплового потока за время dt

,

где - градиент температуры, знак «минус» показывает, что энергия переносится в направлении убывания температуры.

ЭЛЕКТРОСТАТИКА

· Закон Кулона

где F – модуль силы взаимодействия двух точечных зарядов q₁ и q₂; r – расстояние между зарядами; e₀ =8,85×10^-12 Ф/м – электрическая постоянная, 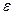-диэлектрическая проницаемость вещества (для вакуума )

· Напряженность и потенциал электростатического поля

; , или ,

где 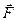- сила, действующая на точечный положительный заряд , помещенный в данную точку поля; - потенциальная энергия заряда ; - работа по перемещению заряда из данной точки поля за пределы поля.

· Напряженность и потенциал электростатического поля точечного заряда 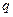на расстоянии 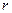от заряда

; .

· Поток вектора напряженности через площадку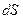

,

где - вектор, модуль которого равен 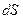, а направление совпадает с нормалью 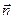к площадке; - составляющая вектора по направлению нормали 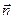к площадке ( ), 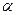-угол между векторами и .

· Поток вектора напряженности через произвольную поверхность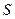

.

· Поток вектора напряжённости через замкнутую поверхность (рис.12)

.

Рис.12

· Принцип суперпозиции (наложения) электростатических полей

; ,

где , - соответственно напряженность и потенциал поля, создаваемого зарядом .

· Направление вектора напряжённости , создаваемого точечным зарядом (рис.13)

Рис.13

ПРИМЕР. Найти напряженность электрического поля, созданного двумя разноимёнными зарядами в точках А, В и С (рис.14)

Рис.14

В точке А: Е=Е₁+ Е₂

В точке В: Е=Е₁ – Е₂

В точке С: Е=

· Связь между напряженностью и потенциалом электростатического поля

, или ,

где , , - единичные векторы координатных осей.

· Вектор напряженности направлен в сторону убывания потенциала (рис.15)

Рис.15

· Направление вектора градиента потенциала в точке А (рис.16)

Рис.16

· В случае поля, обладающего центральной или осевой симметрией

.

· Эквипотенциальные поверхности – геометрическое место точек с одинаковым потенциалом. Вектор напряжённости направлен по нормали к эквипотенциальной поверхности.

· Электрический момент диполя (дипольный момент)

,

где - плечо диполя, О – центр диполя (рис.17).

Рис.17

Напряжённость поля на продолжении оси диполя на расстоянии от центра диполя r>>l

.

Напряжённость поля на перпендикуляре, восстановленном к оси из его середины на расстоянии r>>l

.

· Линейная, поверхностная и объемная плотности зарядов, т.е. заряд, приходящийся соответственно на единицу длины, поверхности и объема:

; ; .

· Теорема Гаусса для электростатического поля в вакууме

,

где - алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; N – число зарядов.

Если заряд распределён внутри замкнутой поверхности непрерывно с объёмной плотностью , то

Примеры: 1.Определить поток Ф_Е вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечный заряд (рис.18).

Рис.18

По теореме Гаусса .

2. Как изменится поток через ту же поверхность, если внутрь поместить ещё один заряд (рис.19)?

Рис.19

По теореме Гаусса , т.е. поток уменьшится вдвое и станет отрицательным.

3. Как изменится поток через данную поверхность, если около неё поместить любой заряд 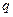(рис.20)?

Рис.20

Поток не изменится, т.к. заряд находится вне поверхности.

· Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью,

.

· Напряжённость поля, создаваемого двумя бесконечными параллельными разноимённо заряженными плоскостями

- между плоскостями,

- вне плоскостей.

· Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R с общим зарядом q на расстоянии r от центра сферы,

E = 0 при r < R (внутри сферы);

при r ³ R (вне сферы).

· Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром (нитью) радиусом R на расстоянии r от оси цилиндра,

E = 0 при r < R (внутри цилиндра);

при r ³ R (вне цилиндра).

· Работа, совершаемая силами электростатического поля при перемещении заряда q₀ из точки 1 в точку 2,

, или ,

где - проекция вектора на направление элементарного перемещения , и - потенциалы электростатического поля в точках 1 и 2.

· Работа сил электростатического поля не зависит от вида траектории, а определяется только начальным и конечным положениями, по замкнутому пути работа равна нулю.

· Циркуляция вектора напряжённости электростатического поля равна нулю, следовательно это поле потенциальное

.

Это значит, что линии напряжённости электростатического поля начинаются и заканчиваются на зарядах.

· Вектор поляризации диэлектрика:

,

где V – объем диэлектрика; - дипольный момент i-й молекулы.

· Связь между векторами поляризации и напряженности электростатического поля внутри диэлектрика
æe_{0 ,}

где æ – диэлектрическая восприимчивость вещества.

· Связь диэлектрической проницаемости e с диэлектрической восприимчивостью æ

e = 1 + æ.

· Связь между напряженностью поля в диэлектрике и напряженностью внешнего поля

, или .

· Связь между векторами электрического смещения и напряженностью электростатического поля

.

· Связь между векторами электростатического смещения ( ), напряжённости поля ( ) и поляризации ( )

.

· Теорема Гаусса для электростатического поля в диэлектрике

,

где - алгебраическая сумма заключенных внутри замкнутой поверхности 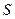свободных электрических зарядов; - составляющая вектора по направлению нормали 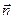к площадке ; - вектор, модуль которого равен 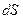, а направление совпадает с нормалью 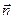к площадке. Интегрирование ведется по всей поверхности.

· Электроемкость уединенного проводника и конденсатора

, ,

где 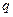- заряд, сообщенный проводнику; 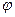- потенциал проводника; – разность потенциалов между пластинами.

· Электроемкость плоского конденсатора

,

где 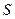- площадь каждой пластины конденсатора; 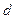- расстояние между пластинами.

· Электроемкость цилиндрического конденсатора

,

где 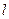- длина обкладок конденсатора; и - радиусы внутренней и внешней обкладок конденсатора.

· Электроемкость сферического конденсатора

,

где и - радиусы сферических обкладок конденсатора.

· Электроемкость системы конденсаторов соответственно при последовательном (а) и параллельном (б) соединениях

а) , б) ,

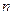где - электроемкость - го конденсатора; - число конденсаторов.

· Энергия уединенного заряженного проводника

.

· Потенциальная энергия системы точечных зарядов
,

где j_{i –} потенциал, создаваемый в той точке, где находится заряд q_i , всеми зарядами, кроме i-го.

· Энергия заряженного конденсатора

,

где q – заряд конденсатора; C – его емкость; U - разность потенциалов между обкладками.

· Сила притяжения между обкладками плоского конденсатора

.

· Энергия электростатического поля плоского конденсатора
,

где S – площадь одной пластины; U – разность потенциалов между пластинами; V=Sd – объем области между пластинами конденсатора.

· Объемная плотность энергии электростатического поля
,

где D – электрическое смещение, 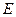-напряжённость поля.

· Если конденсатор заряжен до разности потенциалов ( ) и отключенот источника тока, то при изменении расстояния между пластинами заряд на них неизменен,т.е. .

А если конденсатор не отключен от источника тока, то при изменении расстояния между пластинами неизменнаразность потенциалов на нем, т.е. .