Соотношение неопределённостей Гейзенберга
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга.
Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей: 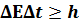
Это соотношение означает, что определение энергии с точностью должно занять интервал времени, равный, по меньшей мере,
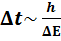
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Соотношение неопределенностей указывает, в какой мере возможно пользоваться понятиями классической механики применительно к микрочастицам, в частности с какой степенью точности можно говорить о траекториях микрочастиц. Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив в (4.2.1) вместо произведение , получим соотношение: 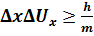
Из этого соотношения следует, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости, следовательно тем с большей точностью можно применять к этой частице понятие траектории.
Уравнение Шредингера.
В 1925 г. австрийский физик Эрвин Шрёдингер сконструировал дифференциальное уравнение для волновой функции де-Бройля (подробнее см. [1], с.с. 137-178). 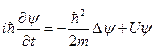 . Общее уравнение Шрёдингера (4.1)
. Общее уравнение Шрёдингера (4.1)
Здесь  – мнимая единица, ħ=hç2π, m – масса частицы, U– потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа.
– мнимая единица, ħ=hç2π, m – масса частицы, U– потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа.
Для систем в стационарном состоянии, когда все наблюдаемые физические параметры не меняются с течением времени, уравнение Шрёдингера имеет вид:
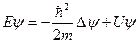 . Уравнение Шрёдингера для стационарных состояний (4.2)
. Уравнение Шрёдингера для стационарных состояний (4.2)
Здесь E – полная энергия системы, постоянная величина.
Операторы физических величин.
Квантование энергии и момента импульса.
Квантовые числа.
Собственные функции уравнения Шрёдингера для атома, т.е. Ψ-функции содержат, как выяснилось, три целочисленных параметра – n, l, m :
Ψ = Ψnlm( r, θ, φ )
n - главное квантовое число ( то же, что и в выражениях для Еп )
п = 1; 2; 3; …
l – орбитальное (азимутальное) квантовое число, определяющее модуль орбитального момента импульса движущегося в атоме электрона.
В квантовых состояниях с заданным значением главного квантового числа п орбитальное квантовое число может иметь следующие значения:
l = 0; 1; 2; 3; … ; (п – 1).
Орбитальное квантовое число l однозначно определяет модуль орбитального момента импульса движущегося в атоме электрона: