Электростатика. Диэлектрики
Примеры решения задач
23. По тонкому кольцу равномерно распределен заряд Q = 40 нКл с линейной плотностью  = 50 нКл/м. Определить напряженность
= 50 нКл/м. Определить напряженность  электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
Дано: Q = 40 нКл =  Кл Кл 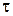 = 50 нКл/м = = = 50 нКл/м = =  Кл/м h = Кл/м h =  |
 |


Напряженность поля, создаваемого этим зарядом 
где  – электрическая постоянная;
– электрическая постоянная;  – единичный вектор, направленный вдоль r . Разложим вектор
– единичный вектор, направленный вдоль r . Разложим вектор  на две составляющие:
на две составляющие:  вдоль оси Z, и
вдоль оси Z, и  , перпендикулярную оси z ,т.е.
, перпендикулярную оси z ,т.е.


 .
.
Напряжённость  электрического поля в точке А найдём интегрированием
электрического поля в точке А найдём интегрированием


 ,
,
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dQ и d  , расположенных симметрично относительно центра кольца, векторы
, расположенных симметрично относительно центра кольца, векторы  и
и  , в точке А равны по модулю и противоположны по направлению
, в точке А равны по модулю и противоположны по направлению  = –
= –  , т.е компенсируют друг друга.
, т.е компенсируют друг друга.
Составляющие  для всех элементов кольца сонаправлены с осью z, т.е.
для всех элементов кольца сонаправлены с осью z, т.е.  =
=  .
.
Тогда 
Так как  ,
,  ;
;  , то
, то
 .
.
Таким образом  .
.
Поскольку  , то радиус кольца
, то радиус кольца  .
.
Тогда  .
.
Значение напряженности на расстоянии z = h = R/2.
 = 7000 В/м = 7,9 кВ/м
= 7000 В/м = 7,9 кВ/м
Ответ: Е = 7,9 кВ/м.
24. Электрическое поле создается бесконечным цилиндром радиусом R, равномерно заряженным с линейной плотность τ. Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии  и
и  от поверхности этого цилиндра. Решение
от поверхности этого цилиндра. Решение
 | |||
 | |||
               Дано Дано           R R       τ τ               |
       φ1 – φ2 ? φ1 – φ2 ? |
Интегрирал по гауссовой поверности, верхности раскладываем на три интеграла: по верхнему и нижнему основаниям, по боковой поверхности. Интеграл по верхнему основанию  , так как угол
, так как угол  между вектором элементарной площадки
между вектором элементарной площадки  и вектором
и вектором  равен π /2 и cos π /2 = 0. Аналогично для нижнего основания. Остается интеграл по боковой поверхности
равен π /2 и cos π /2 = 0. Аналогично для нижнего основания. Остается интеграл по боковой поверхности  , здесь угол
, здесь угол  = 0, cos 0 = 1, значение напряженности Е на одном и том же расстоянии r одинаково, Е выносим за знак интеграла
= 0, cos 0 = 1, значение напряженности Е на одном и том же расстоянии r одинаково, Е выносим за знак интеграла  . В правой части теоремы Гаусса заряд, охватываемый гауссовой поверхностью
. В правой части теоремы Гаусса заряд, охватываемый гауссовой поверхностью  . Таким образом, получаем
. Таким образом, получаем


Для нахождения разности потенциалов воспользуемся связью напяженности и потенциала
 .
.
Для случая радиальной симметрии, реализующейся у нас,
 .
.
Интегрируя это выражение, получим
 или
или
 .
.
Ответ:  .
.
25. Плоский конденсатор, между обкладками которого помещена стеклянная пластинка 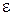 (
( 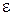 = 6) толщиной l = 2,00 мм, заряжен до напряжения U = 200 В (рис. 1). Пренебрегая величиной заряда между пластинкой и обкладками, найти а) поверхностную плотность
= 6) толщиной l = 2,00 мм, заряжен до напряжения U = 200 В (рис. 1). Пренебрегая величиной заряда между пластинкой и обкладками, найти а) поверхностную плотность  свободных зарядов на обкладках конденсатора, а также б) поверхностную плотность
свободных зарядов на обкладках конденсатора, а также б) поверхностную плотность  связанных зарядов (зарядов поляризации) на стекле. Изобразить силовые линии электрического поля в стекле и воздушном зазоре между стеклом и обкладками.
связанных зарядов (зарядов поляризации) на стекле. Изобразить силовые линии электрического поля в стекле и воздушном зазоре между стеклом и обкладками.
 Дано: Дано:
U = 200 В | ||
σ – ? σ´ – ?  силовые линии Е силовые линии Е |
 (1)
(1)
Отсюда, учитывая соотношение Е =  , справедливое для однородного поля конденсатора, найдем:
, справедливое для однородного поля конденсатора, найдем:
 (2)
(2)
Чтобы определить величину  , воспользуемся формулой
, воспользуемся формулой  =
=  (поверхностная плотность связанных зарядов равна проекции вектора поляризованности
(поверхностная плотность связанных зарядов равна проекции вектора поляризованности  на внешнюю нормаль к поверхности диэлектрика). Так как вектор
на внешнюю нормаль к поверхности диэлектрика). Так как вектор  параллелен вектору напряженности
параллелен вектору напряженности  поля в диэлектрике, направленному по нормали к поверхности стеклянной пластинки, то
поля в диэлектрике, направленному по нормали к поверхности стеклянной пластинки, то  =
=  . Учитывая соотношение
. Учитывая соотношение  = æ
= æ  , где æ – диэлектрическая проницаемость среды и соотношение
, где æ – диэлектрическая проницаемость среды и соотношение  æ, получим:
æ, получим:
 æ
æ  (3)
(3)
Подставляя в формулы (2) и (3) величины в единицах СИ: U = 200 B,  = 2,00
= 2,00  м,
м,  = 8.85
= 8.85  Ф/м, найдем:
Ф/м, найдем:
 =
= 
 =
= 
 Чтобы изобразить силовые линии электрического поля в стекле и воздуш ном зазоре, надо помнить, что густота силовых линий пропорциональна напряженности поля, а диэлектрическая проницаемость среды
Чтобы изобразить силовые линии электрического поля в стекле и воздуш ном зазоре, надо помнить, что густота силовых линий пропорциональна напряженности поля, а диэлектрическая проницаемость среды  показывает во сколько раз поле внутри диэлектрика слабее поля внутри зазора, следовательно густота силовых линий внутри стеклянной пластинки в шесть раз меньше, чем в зазоре (рис. 2).
показывает во сколько раз поле внутри диэлектрика слабее поля внутри зазора, следовательно густота силовых линий внутри стеклянной пластинки в шесть раз меньше, чем в зазоре (рис. 2).
Ответ:  =
= 
 =
= 
26. Определить дивергенцию следующих векторных полей:
a)  , где f(x) – некоторая функция декартовой координаты х;
, где f(x) – некоторая функция декартовой координаты х;
b)  , где
, где  – радиус-вектор точки, в которой определяется дивергенция.
– радиус-вектор точки, в которой определяется дивергенция.
Дано: а)  ; b) ; b)  | Решение По определению  . a) . a)  ; b) Выразим радиус-вектор через компоненты: ; b) Выразим радиус-вектор через компоненты: |
div  - ? - ? |
 ,
,
 .
.
Ответ:а)  ; b) div
; b) div  = 3.
= 3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1. Шар радиусом R заряжен однородно с объёмной плотностью r. Найти напряженность поля  для точек внутри и вне шара.
для точек внутри и вне шара.
(  ;
;  )
)
3.2. Бесконечно тонкая прямая нить заряжена однородно с плотностью l. Найти напряженность электрического поля Е и потенциал j как функции расстояния r от нити. Потенциал на расстоянии r0 положить равным нулю.
(E = (1/2pe0) l/r; j = -(l/2pe0) ln(r/r0))
3.3. Тонкий длинный стержень равномерно заряжен с линейной плотностью t = 1,5 нКл/см. На продолжении оси стержня на расстоянии d = 12 см от его конца находится точечный заряд Q = 0,20 мкКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
(F = 2,2 мН)
3.4. По тонкому проволочному кольцу радиусом r = 60 мм равномерно распределен заряд q = 20 нКл.
а) приняв ось кольца за ось х, найти потенциал j и напряженность поля  на оси кольца как функцию х (начало отсчета х поместить в центр кольца);
на оси кольца как функцию х (начало отсчета х поместить в центр кольца);
б) исследовать случаи х = 0 и ½х½>> r.
(E = (1/4pe0)×  ; j = (1/4pe0)
; j = (1/4pe0)  )
)
3.5. Чему равен поток вектора  через поверхность сферы, внутри объема которой находится:
через поверхность сферы, внутри объема которой находится:
а) заряд е;
б) заряд -е;
в) диполь с моментом  ?
?
Объясните результат с помощью картины силовых линий электрического поля.
3.6. Металлический шар радиусом R помещен в однородное электрическое поле. Изобразите качественную картину силовых и эквипотенциальных линий электрического поля.
3.7. Два точечных заряда +е и -е расположены в точках с координатами (а/2,0,0), (-а/2,0,0). Построить качественно график зависимости проекции напряженности поля Ех(х) для точек, лежащих на оси х (у = 0).
3.8. Найти зависимость плотности зарядов от декартовых координат ρ(x,y, z), при которой напряженность поля описывалась бы функцией  (В/м).
(В/м).
(ρ(x,y, z) =  Кл/м3)
Кл/м3)
3.9. Потенциал поля, создаваемого некоторой системой зарядов, имеет вид: j = a(x2+y2)-bz2, где а и b – положительные константы. Найти напряженность поля Е и ее модуль ½Е½. Построить графики зависимости Ex = f(x), Ez = f(z).
(E =  ;
;  )
)
3.10. Плоский воздушный конденсатор подключили к батарее, а затем отключили от неё. После этого уменьшим расстояние между пластинами конденсатора в 2 раза. Как изменится:
а) энергия, запасенная конденсатором;
б) заряд на обкладках конденсатора;
в) плотность энергии электрического поля конденсатора?
3.11. Диэлектрическая пластина шириной 2а с проницаемостью e = 2 помещена в однородное электрическое поле напряженности Е, силовые линии которого перпендикулярны пластине.
а) изобразите на рисунке линии полей Е и D электрического поля;
б) постройте качественно графики зависимостей Ех, Dх от х (ось х перпендикулярна пластине, вектор Е направлен вдоль оси х, точка х = 0 находится в середине пластины).
3.12. Диэлектрическая пластинка с проницаемостью e = 2 помещена в однородное электрическое поле с напряженностью Е. Линии поля Е образуют некоторый угол j с поверхностью пластины. Изобразите качественно линии полей Е и D в вакууме и в пластине. Постройте качественно графики зависимостей Еx = f(x) и Dx = f(x).
3.13. Внутри плоской однородной диэлектрической пластины с e = 3 вектор напряженности однородного электрического поля составляет угол j с поверхностью пластины. Считая, что с одной стороны пластины вакуум, а с другой стороны диэлектрик с e = 2, изобразить качественно линии Е и D электрического поля в трех указанных средах. Построить качественно зависимости Еx = f(x) и Dx = f(x). Ось ОХ перпендикулярна поверхностям пластины, а ее толщина d.
3.14. Плоский воздушный конденсатор опустили в воду так, что поверхность воды параллельна плоскостям пластин, а ее уровень расположен на расстоянии h от нижней пластины. Найти зависимость электроемкости конденсатора от величины h, если площадь пластины S, а расстояние между ними d.
(С =  )
)
3.15. Электрическое поле создается равномерно заряженным шаром радиусом R с объемной плотностью заряда r. Определить зависимость вектора электрического смещения электрического поля от r. Построить качественно график D = f(r).
(D = (1/3)rr; D = (r/3)×(R3/r2))
Постоянный ток
Примеры решения задач
27. Пространство между пластинами плоского конденсатора заполнено многослойным диэлектриком, обладающим слабой электропроводностью. Диэлектрическая проницаемость диэлектрика 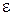 монотонно уменьшается от пластины 1 от значения
монотонно уменьшается от пластины 1 от значения  до значения
до значения  у пластины 2. Удельная электропроводность
у пластины 2. Удельная электропроводность  монотонно уменьшается от пластины 1 от значения
монотонно уменьшается от пластины 1 от значения  Ом.-1 м-1 до значения
Ом.-1 м-1 до значения  Ом.-1 м-1 у пластины 2. Конденсатор включен в цепь с постоянной ЭДС, и в нем устанавливается постоянный электрический ток силой
Ом.-1 м-1 у пластины 2. Конденсатор включен в цепь с постоянной ЭДС, и в нем устанавливается постоянный электрический ток силой  А, текущий через диэлектрик от стороны 1 конденсатора к стороне 2. Найти величину свободного заряда
А, текущий через диэлектрик от стороны 1 конденсатора к стороне 2. Найти величину свободного заряда  , возникшего в диэлектрике при протекании тока.
, возникшего в диэлектрике при протекании тока.
Дано:    Ом.-1м-1 Ом.-1м-1  Ом.-1м-1 Ом.-1м-1  А А | Решение Среда между пластинами конденсатора обладает как электропроводящими, так и диэлектрическими свойствами. Поэтому в решении используется закон Ома в дифференциальной форме:  , (1) где , (1) где  – плотность тока; – плотность тока;  - напряженность электрического поля, и теорема Гаусса для диэлектрика. Направление линий тока вектора - напряженность электрического поля, и теорема Гаусса для диэлектрика. Направление линий тока вектора  и направления векторов и направления векторов |
 – ? – ? |
электрического смещения  и
и  у пластины 1 и пластины 2 соответственно показаны на рисунке.
у пластины 1 и пластины 2 соответственно показаны на рисунке.

Ток через среду постоянный, линии тока перпендикулярны к пластинам конденсатора, следовательно, для величин силы тока у пластины 1 и пластины 2 можно записать

где  - площадь пластины конденсатора. Это же соотношение с учетом закона Ома (1) принимает форму
- площадь пластины конденсатора. Это же соотношение с учетом закона Ома (1) принимает форму
 (2)
(2)
Для использования теоремы Гаусса проведем гауссову поверхность в виде прямоугольного параллелепипеда (пунктирная линия на рисунке), так, чтобы внутри находился диэлектрик. По теореме Гаусса для диэлектрика, учитывая направление векторов  , имеем:
, имеем:
 (3)
(3)
Связь между вектором электрического смещения  и напряженностью
и напряженностью  электрического поля, как известно имеет вид:
электрического поля, как известно имеет вид:
 (4)
(4)
Из соотношений (2) – (4) для величины заряда  следует
следует

 Кл.
Кл.
Ответ:  нКл.
нКл.
28. В схеме, изображенной на рисунке  В,
В,  В,
В,  В,
В,  Ом,
Ом,  Ом,
Ом,  Ом. Внутреннее сопротивление источников тока пренебрежимо мало. Определить силы токов
Ом. Внутреннее сопротивление источников тока пренебрежимо мало. Определить силы токов  ,
,  ,
,  , текущих через сопротивления.
, текущих через сопротивления.
Дано:  В В  В В  В В  Ом Ом  Ом Ом  Ом Ом | Решение   | |
 – ? – ?  – ? – ?  – ? – ? | ||
Представленная в задаче схема постоянного тока, может быть рассчитана на основе законов Кирхгофа. Для применения законов Кирхгофа выделим два замкнутых контура АBCDА и AFЕBА. Зададим направление обхода этих замкнутых контуров по часовой стрелке, как показано на рисунке. Также будем рассматривать узел схемы А, в котором сходятся (или вытекают) токи  ,
,  ,
,  .
.
По первому закону Кирхгофа для токов узла А следует уравнение:
 (1)
(1)
В данном выражении учитывалось правило знаков: ток втекает в узел – положителен, ток вытекает из узла – отрицателен.
По второму закону Кирхгофа для контуров ABCDА и AFЕBА имеем соответственно:
 (2)
(2)
 . (3)
. (3)
В выражениях (2) и (3) учитывалось правило знаков, определяемое выбранным направлением обхода контура. ЭДС положительна, если направление обхода контура совпадает с направлением ЭДС.
Подставляя известные численные значения сопротивлений участков цепи и ЭДС источников тока в уравнения (1) – (3), получим
 (4)
(4)
Таким образом, получается система трех линейных уравнений с тремя искомыми неизвестными  ,
,  ,
,  . Решение такой системы дается формулами Крамера:
. Решение такой системы дается формулами Крамера:
 ,
,  ,
,  , (5)
, (5)
где 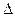 – определитель системы (4);
– определитель системы (4);  – определитель при первом неизвестном
– определитель при первом неизвестном  ;
;  – определитель при втором неизвестном
– определитель при втором неизвестном  ;
;  – определитель при третьем неизвестном
– определитель при третьем неизвестном  .
.
По значениям коэффициентов системы уравнений (4) следует:

 (6),
(6), 
 (7)
(7)

 (8),
(8), 
 (9)
(9)
Из выражений (5) – (9) для величин сил токов получается
 А,
А,  А,
А,  А.
А.
Ответ:  А;
А;  А;
А;  А.
А.
29. Сила тока в проводнике убывает со временем по закону  (
(  А,
А,  с-1). Определить заряд, прошедший через поперечное сечение проводника за время
с-1). Определить заряд, прошедший через поперечное сечение проводника за время  с.
с.
Дано:   А А  с-1 с-1  с с | Решение Величина силы тока  связана с зарядом q, проходящим через поперечное сечение проводника, соотношением связана с зарядом q, проходящим через поперечное сечение проводника, соотношением  . (1) Следовательно, за бесконечно малый промежуток времени . (1) Следовательно, за бесконечно малый промежуток времени  через поперечное сечение проводника пройдет заряд через поперечное сечение проводника пройдет заряд |
 – ? – ? |
 (2)
(2)
Величина заряда q, прошедшего через поперечное сечение проводника за промежуток времени 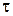 , может быть найдена интегрированием выражения (2):
, может быть найдена интегрированием выражения (2):
 Кл.
Кл.
Ответ:  Кл.
Кл.
30. В медном проводнике объемом  см3 при прохождении по нему постоянного тока за время
см3 при прохождении по нему постоянного тока за время  ,0 мин выделилось количество теплоты
,0 мин выделилось количество теплоты  Дж. Найти напряжённость
Дж. Найти напряжённость  электрического поля в проводнике, плотность тока
электрического поля в проводнике, плотность тока  , скорость упорядоченного движения электронов
, скорость упорядоченного движения электронов  . Считать, что на каждый атом меди приходится один свободный электрон.
. Считать, что на каждый атом меди приходится один свободный электрон.
Проводимость, плотность и молярная масса меди соответственно  ,
, 
Дано: 6,0 см3 =  ,0×10-6 м3 ,0×10-6 м3  мин = 60 с мин = 60 с  Дж Дж  Ом-1×м-1 Ом-1×м-1  Кг/м3 Кг/м3  г/моль = 63,5×10-3 кг/моль г/моль = 63,5×10-3 кг/моль | Решение а) для решения используем закон Ома в дифференциальной форме  , (1) закон Джоуля – Ленца в дифференциальной форме , (1) закон Джоуля – Ленца в дифференциальной форме  (2) где (2) где  – удельная электропроводность меди, – удельная электропроводность меди,  – удельная тепловая мощность тока. Из формул (1) и (2) для напряженности – удельная тепловая мощность тока. Из формул (1) и (2) для напряженности  электрического поля в проводнике следует: электрического поля в проводнике следует: | |
а)  – ? б) – ? б)  – ? в) – ? в)  - ? - ? | ||
 В/м.
В/м.
б) из выражения (1) для плотности тока  имеем
имеем
 А·м-2.
А·м-2.
в) скорость упорядоченного движения электронов  и плотность тока
и плотность тока  связана соотношением
связана соотношением
 , (3)
, (3)
где  – заряд электрона;
– заряд электрона; 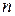 – концентрация свободных электронов. Учитывая, что на каждый атом меди приходится один свободный электрон, для концентрации свободных электронов получается
– концентрация свободных электронов. Учитывая, что на каждый атом меди приходится один свободный электрон, для концентрации свободных электронов получается
 , (4)
, (4)
где  – число Авогадро.
– число Авогадро.
Из формул (3) и (4) для скорости упорядоченного движения электронов следует
 м/c
м/c
Ответ: а)  В/м , б)
В/м , б)  А·
А·  , в)
, в)  м/c.
м/c.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.16. Зазор между обкладками плоского конденсатора заполнен веществом с проницаемостью e = 7 и удельным сопротивлением r = 100 ГОм×м. Емкость конденсатора С = 3000 пФ. Найти силу тока утечки через конденсатор при подаче на него напряжения U = 2000 В.
(I = 9,7×10-7A)
3.17. В схеме, изображенной на рисунке, e1 = 10 В, e2 = 20 В, e3 = 30 В, R1 = 1,0 Ом, R2 = 2,0 Ом, R3 = 3,0 Ом, R4 = 4,0 Ом, R5 = 5,0 Ом, R6 = 6,0 Ом, R7 = 7,0 Ом. Внутреннее сопротивление источников тока пренебрежимо мало. Найти силы токов I1, I2, I3.
 |
(I1 = -1,02 A, I2 = 0,90 A, I3 = -0,12 A)
3.18. Определить заряд Q, прошедший по проводу с сопротивлением R = 3,0 Ом при равномерном нарастании напряжения на концах провода от U0 = 2,0 B до U = 4,0 B в течение 20 с.
(Q = 20 Кл)
3.19. Сила тока в проводнике сопротивлением 20 Ом нарастает в течение времени Dt = 2,0 с по линейному закону от I0 = 0 до Imax = 6,0 A. Определить количество теплоты Q, выделившееся в этом проводнике за первую секунду.
(Q = 60 Дж)
3.20. Концентрация электронов проводимости в меди n = 1,0·1029 м-3. Считая условия нормальными, определить среднее время между двумя столкновениями электрона с решеткой (среднее время свободного пробега). Определить среднюю длину свободного пробега электрона. Удельное сопротивление меди r = 1,7×10-8 Ом×м.
(l = 4,7×10-9 м)
3.21. По медному проводнику сечением 0,20 мм2 течет ток. Определить, какая сила действует на отдельный электрон проводимости со стороны электрического поля, если объемная плотность энергии, выделяемая в проводнике, равна 9,0×103 Дж/м3. Определить плотность и силу тока в проводнике.
F = 20×10-22 H; j = 7,3×105 A/м2; I = 0,15 A)
3.22. Два источника тока, соединенные одинаковыми полюсами, с ЭДС  и
и  и внутренними сопративлениями
и внутренними сопративлениями  и
и  включены параллельно сопративлению R = 2,0 Ом. Определите силу тока через это сопративление.
включены параллельно сопративлению R = 2,0 Ом. Определите силу тока через это сопративление.
(I = 0,78 A)
Магнетизм
Примеры решения задач
 31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток
31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток  А. Найти магнитную индукцию
А. Найти магнитную индукцию  в точках М и N, если
в точках М и N, если  см.
см.

 =
=  , с учетом наличиия диэлектрика
, с учетом наличиия диэлектрика  = 6,0
= 6,0 = 2,00 мм
= 2,00 мм