Молекулярные скорости

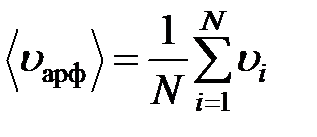
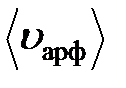В молекулярной физике используют следующие скорости движения молекул:

Средняя арифметическая скоростьмолекул:

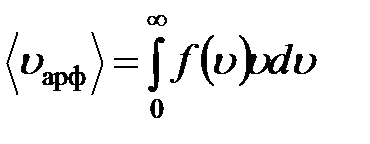Среднюю арифметическую скорость можно найти, используя закон распределения молекул по скоростям:

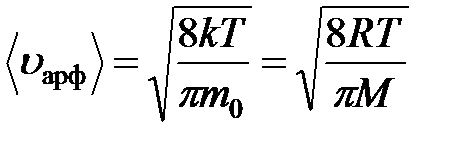Подставив выражение для функции Максвелла и проинтегрировав, получим:

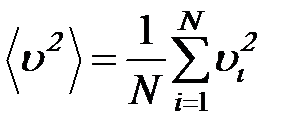
Среднее значение квадрата скорости молекул газа:

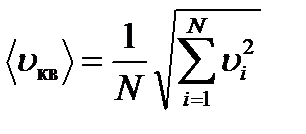
Средняя квадратическая скорость молекул газа:

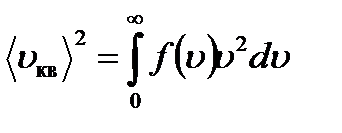
Подставив f(u), проинтегрировав и извлекая корень, получим:

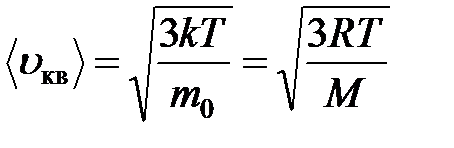
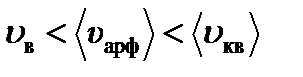Все три скорости незначительно отличаются друг от друга множителем порядка единицы, причем:

Формула Максвелла для относительных скоростей.

Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена в относительных единицах. Такая скорость называется относительной.

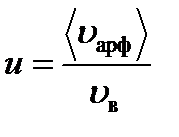Относительная скорость – это скорость, характеризующаяся отношением средней арифметической скорости к наивероятнейшей.

Относительную скорость обозначим через u:

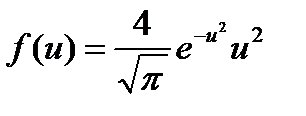Тогда получим

Это уравнение универсальное. В таком виде функция распределения молекул по скоростям не зависит ни от рода газа, ни от температуры.

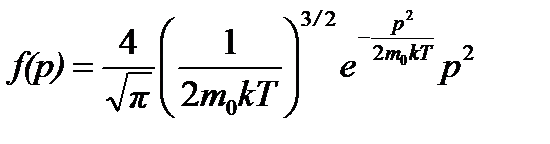Формулы распределения молекул по импульсам и кинетическим энергиям имеют схожий вид с формулой распределения по скоростям.

Распределение молекул по импульсам:

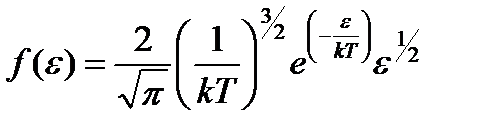Распределение молекул по кинетическим энергиям поступательного движения:

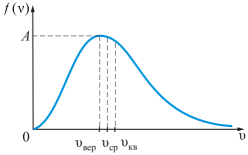
Зависимость функции распределения Максвелла от температуры газа.

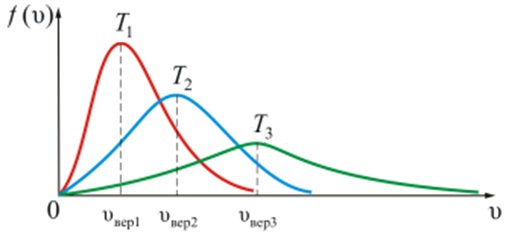
На рисунке показана зависимость f(υ) при различных температурах T₁<T₂<T₃(при m=const). С увеличением температуры газа максимум кривой смещается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями, уменьшается, а доля молекул с большими скоростями увеличивается.

Площадь под кривой величина постоянная, равная единице (f(υ)=const=1).

Максвелловский закон распределения по скоростии все вытекающие следствия из него справедливы толькодля газа в равновесной системы. Это закон статистический, и выполняется тем лучше, чембольше число молекул.

Опыт Штерна.

Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт явился одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.

Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего атомы начинали испаряться и летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью υ, соответствующей подаваемому на концы нити напряжению. Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее. Стенки цилиндров специально охлаждались, что способствовало «оседанию» попадающих на них атомов. В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щели малого цилиндра.

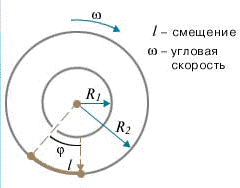
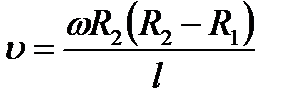
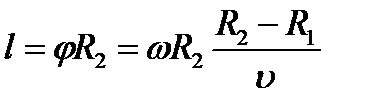
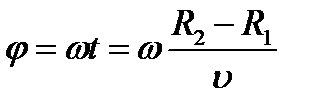
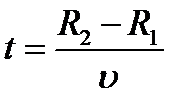Затем всю систему начинали вращать с некой достаточно большой угловой скоростью ω. При этом полоса налёта смещалась в сторону, противоположенную направлению вращения, и теряла чёткость. Измерив смещение s наиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул:

Опыт Ламмерта.

Прямые измерения скорости атомов ртути в пучке были выполнены Ламмертом в 1929 году.

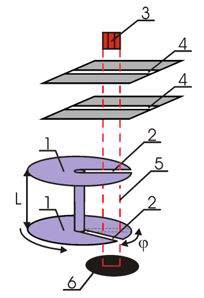
Упрощенная схема опыта Ламмерта:

1 - быстро вращающиеся диски,

2 - узкие щели,

3 - печь,

4 - коллиматор,

5 - траектория молекул,

6 - детектор

Два диска 1, насаженные на общую ось, имели радиальные прорези 2, сдвинутые друг относительно друга на угол φ. Напротив щелей находилась печь 3, в которой нагревался до высокой температуры легкоплавкий металл. Разогретые атомы металла, в данном случае ртути, вылетали из печи и с помощью коллиматора 4 направлялись в необходимом направлении. Наличие двух щелей в коллиматоре обеспечивало движение частиц между дисками по прямолинейной траектории 5, параллельной их оси. Атомы, прошедшие через прорези в дисках, регистрировались с помощью детектора 6. Вся установка помещалась в глубокий вакуум.

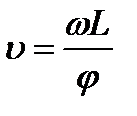При вращении дисков с постоянной угловой скоростью ω, через их прорези беспрепятственно проходили только атомы, имевшие скорость υ:

где L- расстояние между вращающимися дисками.

Опыт Эстермана.

Несколько иначе был организован эксперимент по определению распределения по скоростям для атомов цезия, выполненный в 1947 году немецким физиком-экспериментатором Иммануэлем Эстерманом (1900 - 1973) совместно с О. Симпсоном и Штерном.

На рисунке приведено схематическое изображение опыта Эстермана. Пучок атомов цезия вылетал через отверстие в печи 1 с некоторой скоростью v и под действием силы тяжести начинал двигаться по параболе. Атомы, прошедшие через узкую щель в диафрагме 2, улавливались детектором 3, который можно было располагать на различных высотах h.

Величина отклонения h пучка в гравитационном поле Земли зависела от скорости атома. В этих опытах отклонение h составляло величину порядка нескольких долей миллиметра при расстоянии L от печи до детектора равном 2 метрам. Перемещая датчик и регистрируя количество атомов цезия, попадающих в детектор за единицу времени, можно было построить зависимость интенсивности пучка от величины h. Последующий пересчет, с учетом известной зависимости высоты h от скорости атома υ, давал распределение по скоростям атомов цезия.

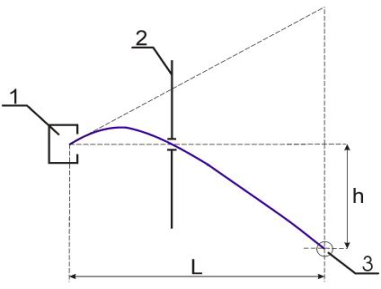
Схема опыта Эстермана:

1 – печь;

2 - диафрагма с узкой щелью;

3 – детектор.

Все проведенные эксперименты подтвердили справедливость полученного Максвеллом распределения по скоростям для атомных и молекулярных пучков.

28. Барометрическая формула. Распределения Больцмана.