Зонная модель полупроводника

Известно, что первичными и единственными носителями заряда являются электроны и протоны. В вакууме и газах электроны и протоны могут быть свободными, в твердых телах и жидкостях электроны и протоны связаны с атомами и их заряды нейтрализуют друг друга.

Полупроводниковые кристаллы образуются из атомов, расположенных в определенном порядке. Естественно возникает вопрос, если в атоме электроны связаны с ядром, то откуда в состоящем из атомов кристалле берутся свободные заряды, способные перемещаться по кристаллу создавая электрический ток. Действительно, если представить атом как изолированный шарик, то тело полученное из миллиардов уложенных в правильном порядке шариков все равно останется изолятором, поскольку в нем способные переносить заряд не появятся. Для того, чтобы объяснить как в металлах и полупроводниках появляются свободные электроны необходимо использовать закономерности микромира. Согласно законам квантовой механики, электроны могут находиться только в строго определенных энергетических состояниях. Изменение энергии электрона возможно при поглощении или испускании кванта электромагнитного излучения с энергией, равной разности значений энергий на начальном и конечном уровне. Поэтому оптические спектры поглощения (или излучения) атомов, соответствующие электронным переходам на свободные дискретные уровни, так же должны быть дискретны, что и наблюдается в экспериментах (рис. 3.4.)

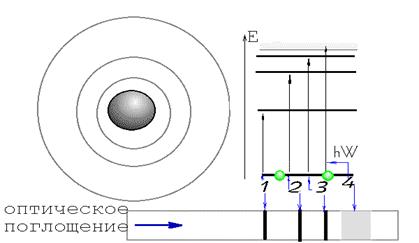Рис. 3.4. Диаграмма, иллюстрирующая энергетический спектр электронов в атоме (модель Бора) и ожидаемый спектр поглощения.

Электронные оболочки принято обозначать буквами и числами (N). Число N называют главным квантовым. Отсчет его значения осуществляется от уровня, ближайшей к ядру N = 1, 2, 3, 4 и т.д., оболочки имеют соответствующие буквенные обозначения: K, L, M, N, и т.д.

На каждой оболочке может находиться несколько электронов, причем каждому из них соответствует свой энергетический уровень, со своим пространственным распределением заряда, который часто называют орбиталью. Энергетические уровни электронов (орбитали) внутри оболочки (с одним числом N) принято обозначать буквами: s (нижний уровень), p, d, f и т.д. Причем чем выше энергия оболочки (больше N), тем большее число электронов может на ней находиться, или другими словами ей соответствует большее число орбиталей. Так первой оболочке соответствует один уровень - орбиталь 1s, т.е. на этой оболочке могут находиться только два электрона с разными спинами. Соответственно конфигурацию с одной оболочкой имеют только два атома – водорода и гелия.

Второй оболочке соответствуют три уровня: одна орбиталь 2s и три орбитали 2p, т.е. в этой оболочке могут находиться шесть электронов.

Третей оболочке соответствуют девять уровней: одна орбиталь 3s, три орбитали 3p, пять орбиталей 3d, т.е. в этой оболочке могут находиться до 18 электронов.

При увеличении числа электронов в атоме, заполнение оболочек происходит по определенным правилам:

1. Первыми заполняются низшие по энергии орбитали.

2. На любой орбитали может находиться не более двух электронов с противоположными значениями спина (принцип запрета Паули).

3. Заполнение орбиталей одной оболочки начинается одиночными электронами с параллельными спинами, пары начинают образовываться только после того как каждая орбиталь имеет по одному электрону (правило Гунда).

Именно на основе правил заполнения оболочек построена периодическая таблица элементов Д.И.Менделеева. Один ряд таблицы соответствует элементам, в которых происходит заполнение внешней (валентной) оболочки, переход от одной ячейке к другой в пределах ряда соответствует добавлению одного электрона.

При сближении двух атомов, например водорода, их орбитали начинают перекрываться и возможно возникновение связи между ними. Существует правило, согласно которому число орбиталей у молекулы равно сумме чисел орбиталей у атомов, при этом взаимодействие атомов приводит к тому, что уровни у молекулы расщепляются, при этом чем меньше расстояние между атомами, тем сильнее это расщепление.

На рис. 3.5 показана схема расщепления уровней для пяти атомов при уменьшении расстояния между ними. Как видно из графиков при образовании между атомами связей валентные электроны формируют разрешенные для электронов зоны, причем число состояний в этих зонах тем больше, чем больше взаимодействующих атомов. В кристаллах число атомов более чем 10²² см^-3, примерно такое же количество уровней в зонах. При этом расстояние между уровнями становится чрезвычайно малым, что позволяет считать, что энергия в разрешенной зоне изменяется непрерывно. Тогда электрон, попавший в незанятую зону можно рассматривать как классический, считая, что под действием электрического поля он набирает непрерывно энергию, а не квантами, т.е. ведет себя как классическая частица.

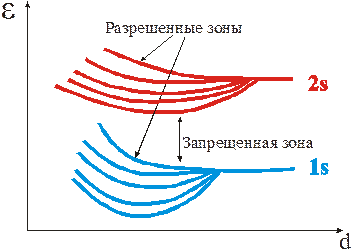
Рис. 3.5. Энергетическое расщепление 1s и 2s уровней для пяти атомов в зависимости от расстояния между ними

При образовании кристаллов образуемые валентными электронами зоны могут быть частично заполненными, свободными или полностью заполненными электронами. При этом если между заполненными и свободными состояниями запрещенная зона отсутствует, то материал является проводником, если существует небольшая запрещенная зона, то это полупроводник, если запрещенная зона большая и электроны за счет тепловой энергии в нее не попадают, то это изолятор. Для проводников разрешенная зона частично заполнена электронами, поэтому даже при приложении внешнего напряжения они способны набирать энергию и перемещаться по кристаллу. Такая структура зон характерна для металлов. Уровень F, разделяющий заполненную электронами и незаполненную часть зоны называют уровнем Ферми. Формально его определяют как уровень вероятность заполнения которого электронами равна 1/2.

Для полупроводников и диэлектриков структура зон такова, что нижняя разрешенная зона полностью заполнена валентными электронами, поэтому ее называют валентной. Потолок валентной зоны обозначают E_v. В ней электроны перемещаться под действием поля (и соответственно набирать энергию) не могут, поскольку все энергетические уровни заняты, а согласно принципу Паули электрон не может переходить с занятого состояния на занятое. Поэтому электроны в полностью заполненной валентной зоны не участвуют в создании электропроводности. Верхняя зона в полупроводниках и диэлектриках в отсутствии внешнего возбуждения свободна от электронов и если каким-либо образом туда забросить электрон, то под действием электрического поля он может создавать электропроводность, поэтому эту зону называют зоной проводимости. Дно зоны проводимости принято обозначать E_c. Между зоной проводимости и валентной зоной находится запрещенная зона E_g, в которой согласно законам квантовой механики электроны находиться не могут (подобно тому как электроны в атоме не могут иметь энергии не соответствующие энергиям электронных оболочек).

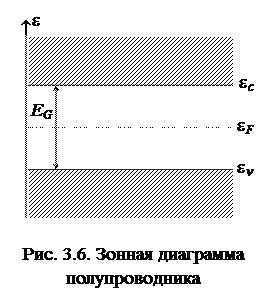Расчет проводимости полупроводников обычно производят на основе зонной модели. Схематическое изображение наиболее важных зон полупроводника представлено на рис. 3.6, где: e_c , e_v и e_F – значения энергии, соответствующие дну зоны проводимости, потолку валентной зоны и уровню Ферми; E_G – ширина запрещенной зоны.

Равновесные концентрации свободных электронов п₀ и дырок р₀ в полупроводнике определяются следующими равенствами:

,

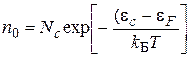(2.1)

,

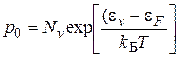где: N_c и N_v – эффективные плотности состояний в зоне проводимости и в валентной зоне (соответственно), k_Б – постоянная Больцмана, Т – абсолютная температура полупроводника. Для кремния N_c » N_v » 2×10¹⁹ см^-3. Энергия Ферми (электрохимический потенциал) фактически равна работе, которую необходимо совершить для изменения числа свободных носителей заряда на единицу. В беспримесном и бездефектном полупроводнике (в собственном полупроводнике) энергия Ферми обозначается e_i и она равна:

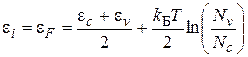. (3.2)

где отношение N_v /N_c приблизительно пропорционально отношению эффективных масс дырки и электрона.

Если за счет термического возбуждения электрон покидает валентную зону, то на его месте в этой зоне образуется дырка. Поэтому собственные концентрации свободных носителей в идеальном беспримесном полупроводники одинаковы и определяются равенством

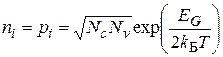, (3.3)

где N_vN_c ~ T ³, а E_G = E_G0 – k_БT. Зависимость E_G от температуры приводит к тому, что при Т = 0 К ширина запрещенной зоны, например, кремния E_G = E_G0= 1,21 эВ, в то время как при комнатной температуре (Т = 300 К) E_G =1,1 эВ.

Практические расчеты концентрации свободных носителей в бездефектном беспримесном полупроводнике для заданной температуры следует вести по формуле

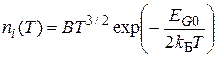, (3.4)

где значения констант для кремния и германия следующие: 1) кремний: В =3,873×10¹⁶ K^-3/2×см^-3, E_G0 = 1,21 эВ; 2) германий: В =1,76×10¹⁶ K^-3/2×см^-3, E_G0 = 0,785 эВ. Используя эту формулу, для кремния при Т = 300 К можно получить n_i(Si) = 1,4×10¹⁰ см^-3 , а для германия n_i(Ge) = 2,3×10¹³ см^-3.

Для целенаправленного изменения проводимости и других физических свойств полупроводника его легируют донорными (фосфор Р, мышьяк As, сурьма Sb) или акцепторными (алюминий Al, галий Ga, индий In) примесями.

Вследствие термического возбуждения постоянно происходит генерация свободных носителей, как за счет переноса электронов из валентной зоны в зону проводимости, так и за счет ионизации донорных и акцепторных атомов. Одновременно с этим происходят рекомбинационные процессы, приводящие к исчезновению свободных носителей. При любой температуре устанавливается такое равновесное состояние, что произведение п×р при неизменных значениях Т и Е_g оказываетсяпостоянным:

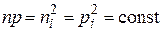(3.5)

Равенство (3.5) называют законом действующих, масс.

Концентрации носителей заряда можно представить в виде функций, зависящих от n_i и E_i:

,

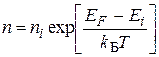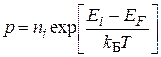. (3.6)

Равенства (3.4) и (3.5) позволяют получить формулу

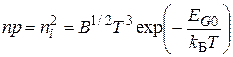. (3.7)

Концентрация носителей заряда определяется положением уровня Ферми. Уровень Е_F для примесного полупроводника с донорной примесью (п-типа), можно найти, используя равенство:

.

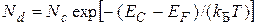В результате находим, что

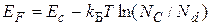. (3.8)

Для полупроводника р-типа справедливо равенство

,

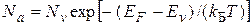откуда

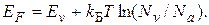(3.9)

В примесных полупроводниках любого типа проводимости (п или р) одновременно присутствуют как свободные электроны, так и дырки. Те из них, которые соответствуют типу проводимости полупроводника, называются основными носителями заряда. Носители противоположного типа называются неосновными. Для определения их концентраций можно использовать следующие формулы:

,

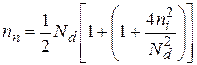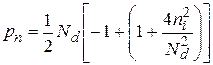. (3.10)

где п_п и р_п – соответственно основные и неосновные носители заряда в полупроводнике п-типа.

В равновесных условиях полупроводник должен быть электронейтрален. Условие электронейтральности представляется равенством:

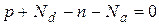, (3.11)

где N_d и N_a соответственно обозначают концентрации донорных и акцепторных атомов.