Обработка результатов измерений. 1. Определить объем воздуха протекающего через капилляр в течении времени t по
1. Определить объем воздуха протекающего через капилляр в течении времени t по формуле:
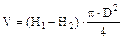
2. Найти разность давлений на концах капилляра:
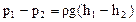 ,
,
где (h1 - h2) - разность уровней воды в манометре, ρ - плотность воды
3. Рассчитать по формуле (9) значение коэффициента динамической вязкости воздуха h и определить погрешность. Сравнить с табличным значением.
4. Для определения средней длины свободного пробега молекул воздуха используется соотношение:
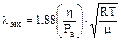 , (10)
, (10)
где m - молярная масса воздуха.
5. Рассчитать среднее значение величины lэкс и ее погрешность.
6. Сравнить 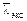 с lтеор =
с lтеор = 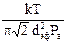 (значения эффективного диаметра молекулы и массу 1 моля воздуха найти в справочнике).
(значения эффективного диаметра молекулы и массу 1 моля воздуха найти в справочнике).
Контрольные вопросы
1. Как определяется средняя длина свободного пробега молекул? Как она зависит от температуры, от давления?
2. Какова природа явлений переноса? Какие явления переноса вы знаете?
3. Записать формулу для потока импульса.
4. Чем обусловлено внутреннее трение (вязкость) газа ?
5. В какой части экспериментальной установки возникает исследуемое в опыте явление переноса?
6. В каком направлении происходит перенос импульса?
7. Определите физический смысл коэффициента динамической вязкости. Как зависит h от давления и температуры газа?
8. Как определяется кинематическая вязкость?
9. Когда возникает сила внутреннего трения? От чего она зависит?
10. Выведите формулу (9) для расчёта коэффициента динамической вязкости.
11. Как определяется объем воздуха, проходящего через капилляр?
12. Как определяется разность давлений, возникающих на концах капилляра?
Лабораторная работа № 7
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ.
Цель работы: Изучение поверхностных явлений, определение коэффициента поверхностного натяжения жидкости методом взвешивания капель и методом отрыва кольца.
Введение
Совокупность явлений, связанных с особыми свойствами поверхностных слоев на границе раздела двух фаз, называют поверхностными явлениями. На границе раздела «жидкость – пар» все молекулы можно разбить на три группы: молекулы газообразной фазы, молекулы внутренних слоев и молекулы поверхностного слоя. Каждая молекула жидкости испытывает притяжение со стороны всех соседних с ней молекул, находящихся в пределах радиуса молекулярного действия r, который имеет значение порядка нескольких эффективных диаметров молекул ~10-9 м. Равнодействующая всех сил притяжения для молекулы М1, находящейся от поверхности жидкости на расстоянии r >10-9 м, очевидно, в среднем равна нулю (рис.1). Молекулы приграничного слоя М2 и М3 окружены соседними молекулами жидкости не со всех сторон. Часть “соседей” на поверхности - это частицы приграничной среды.
 |
Поэтому сила притяжения, испытываемая молекулами поверхностного слоя со стороны молекул жидкости, больше, чем со стороны молекул пара. В результате, равнодействующая всех сил притяжения, действующих на молекулу, находящуюся на поверхности, отлична от нуля и направлена внутрь жидкости. Следовательно, для перехода молекулы из глубинных слоев жидкости на поверхность нужно совершать работу против этой силы, т.е. такой переход требует затрат энергии. Эта работа совершается молекулой за счет запаса ее кинетической энергии и идет на увеличение потенциальной энергии молекулы, подобно тому, как работа, совершаемая летящим вверх телом против сил земного тяготения, идет на увеличение потенциальной энергии тела. При обратном переходе молекулы в глубь жидкости потенциальная энергия, которой обладала молекула в поверхностном слое, переходит в кинетическую энергию молекулы.
Таким образом, молекулы в поверхностном слое обладают дополнительной потенциальной энергией, которая входит составной частью во внутреннюю энергию жидкости. В состоянии равновесия свободная энергия системы должна быть минимальной. Это один из важнейших законов природы его еще называют принципом минимума потенциальной энергии.
Из-за наличия поверхностной энергии жидкость обнаруживает стремление к сокращению своей поверхности. Жидкость ведет себя так, как если бы она была заключена в упругую растянутую пленку, стремящуюся сжаться. Следует иметь в виду, что никакой пленки, ограничивающей жидкость снаружи, на самом деле нет. Поверхностный слой состоит из тех же молекул, что и вся жидкость, и взаимодействие между молекулами имеет в поверхностном слое тот же характер, что и внутри жидкости. Дело заключается лишь в том, что молекулы в поверхностном слое обладают дополнительной энергией по сравнению с молекулами внутри жидкости. Выделим мысленно часть поверхности жидкости, ограниченную замкнутым контуром. Тенденция этого участка к сокращению приводит к тому, что он действует на граничащие с ним участки с силами, распределенными по всему контуру (по третьему закону Ньютона внешние участки поверхностного слоя действуют на рассматриваемую часть поверхности с силами такой же величины, но противоположного направления). Эти силы называются силами поверхностного натяжения. Направлена сила поверхностного натяжения по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует. Обозначим силу поверхностного натяжения, приходящуюся на единицу длины контура, через a. Эту величину называют коэффициентом поверхностного натяжения и измеряют ее в Н/м (СИ).
Если жидкость не ограничена стенками сосуда и не подвержена действию внешних силовых полей (силы тяжести), тогда под действием сил поверхностного натяжения она примет форму шара, т.к. из всех тел данного объема шар имеет наименьшую поверхность. Например, маленькие капли ртути на стекле имеют форму шара. Но с увеличением объема форма их меняется. С увеличением объема увеличивается потенциальная энергия капли и поверхностная энергия. Потенциальная энергия капли пропорциональна объему, а поверхностная энергия пропорциональна площади поверхности, поэтому относительное влияние силы тяжести тем больше, чем больше объем капли.
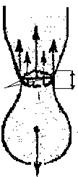 Δℓ d Δℓ d 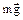 Рис. 2 Рис. 2 |
При постоянной температуре для изменения поверхности жидкости на величину DS необходимо совершить работу. Рассмотрим какой-либо процесс, в ходе которого поверхность жидкости возрастает за счет внешних сил. Это происходит, например, при вытекании жидкости из узкой трубки (рис. 2). Жидкость из такой трубки вытекает по каплям. Непосредственно перед отрывом капля висит на шейке, форму которой можно приблизительно считать цилиндрической. Вес капли уравновешивается силами поверхностного натяжения, действующими по контуру, ограничивающему поперечное сечение шейки:
G = mg = FH
Результирующую этих сил можно представить в виде:
FH = apd, (1)
где d - диаметр шейки. При возрастании длины шейки на Dℓсила тяжести совершает работу:
mgDℓ =pdaDℓ или DА=aDS, (2)
где DS = pdDℓ - приращение поверхности капли, a - коэффициент поверхностного натяжения (a>0). Коэффициент численно равен работе, которую необходимо совершить, чтобы изотермически увеличить площадь поверхности жидкости на единицу при сохранении ее объема. В системе СИ размерность a, в этом случае, равна [Дж/м2].
Поверхностное натяжение зависит от химического состава жидкости и от температуры. Этвеш нашел эмпирическую зависимость коэффициента поверхностного натяжения от температуры:
aVμ 2/3 = K(Tкр - T), (3)
где Ткр – есть критическая температура вещества, Vμ - молярный объем, К – некоторая константа. Из этого выражения следует, что при Т → Ткр a→ 0. В этом случае исчезает различие между жидкостью и ее паром, а значит, исчезает и поверхность, разделяющая обе фазы. Коэффициент поверхностного натяжения зависит и строения жидкости, и от природы молекул газовой фазы над поверхностью жидкости. Это зависимость выражается уравнением Бачинского:
a = С ( ρж – ρп ), (4)
где ρж – плотность жидкости; ρп – плотность насыщенного пара; С – некоторая константа.
Если жидкость находится в сосуде (капилляре) или вне его (рис.3), то из-за различия взаимодействия молекул жидкости между собой и взаимодействием их с молекулами твердого тела наблюдается явление смачивания (рис.3а) или несмачивания (рис.3б), которое приводит к искривлению (увеличению) поверхности жидкости на границе раздела. Искривление поверхности создает дополнительное давление Dр, обусловленное силами поверхностного натяжения, направленное в сторону вогнутости поверхности. Если поверхность (мениск) представляет собой часть сферической поверхности, то добавочное давление Dр определяется по формуле :
Dр = ±2a/R, (5)
где R - радиус кривизны поверхности, знак “+” - для выпуклой поверхности (несмачивание), знак “-“ - для вогнутой (смачивание).
|
Под вогнутым мениском в капилляре давление уменьшается на Dр и жидкость поднимается на высоту Н. Когда гидростатическое давление столбика жидкости уравновесит дополнительное давление, вызванное поверхностным натяжением, подъем столба прекратится.
Упражнение 1. Определение коэффициента поверхностного натяжения методом взвешивания капель
Метод взвешивания капель довольно точный и наиболее распространенный лабораторный метод для измерения поверхностного натяжения на границе раздела: жидкость - воздух; жидкость - жидкость. Измерения заключаются в следующем (рис. 2). На конце трубки формируются капли, их собирают в контейнер до тех пор, пока можно будет достаточно точно определить вес, приходящийся на одну каплю. Простое выражение для определения веса капли G получило известность как закон Тэйта (1864):
G = α πd, (6)
где d – диаметр трубки.
Уравнение (6) выводится из представления о том, что максимальная сила, удерживающая каплю, равна поверхностному натяжению, умноженному на длину окружности кончика трубки. Точность определения этим методом достигается 0,1 %.

