Классификация по взаимодействию между частицами дисперсной фазы
Классификация по агрегатному состоянию дисперсной фазы и дисперсионной среды (по В.Оствальду)
Учитывая, что вещество может находиться в трех агрегатных состояниях, возможны 8 комбинаций дисперсионной среды и ДФ:
| ДС | ДФ | Условное обозначение системы | Тип системы | Примеры |
| Газ | Газ Жидкость Твердое тело | Г–Г Г–Ж Г–Т | Аэрозоли | Нет (гомогенные системы). Туман, облака, аэрозоли жидких лекарств. Дым, пыль, порошки, аэрозоли твердых лекарств. |
| Жидкость | Газ Жидкость Твердое тело | Ж–Г Ж–Ж Ж–Т | Лиозоли | Пены, крем, газированная вода Эмульсии, нефть, молоко, сливки. Суспензии, зубные пасты, тушь, глины. |
| Твердое тело | Газ Жидкость Твердое тело | Т–Г Т–Ж Т–Т | Солидозоли | Твердые пены (пемза, хлеб, резина, лава, пенобетон, пенопласт) Жемчуг, некоторые минеральные гели, опал, желе, желатин, агар-агар Сплавы, стекла, минералы (рубин) |
Для отличия коллоидных растворов от других дисперсных систем, их называют золями (от лат. solutio раствор). Поэтому системы, в которых дисперсионной средой является газ называют аэрозолями, в случае жидкости – лиозолями, в случае твердой дисперсионной среды – солидозолями. В зависимости от природы жидкой дисперсионной среды лиозоли делят на гидрозоли, алказоли, бензозоли, этерозоли (органозоли).
Классификация по взаимодействию дисперсионной среды и дисперсной фазы (по Г.Фрейндлиху)
Такая классификация пригодна только для систем с жидкой дисперсионной средой.
Если поверхность частиц и молекула растворителя имеют одинаковую по-лярность (т.е. сродство), то они будут взаимодействовать друг с другом. Поэто-му вокруг коллоидных частиц образуются толстые многослойные сольватные оболочки. Фрейндлих таких систем назвал лиофильными (от гр. lyo жидкость + phileo люблю). Примерами таких систем являются растворы белка, крахмала, агар-агара, гуммиарабика, высококонцентрированные эмульсии, эмульсолы. В случае, когда частицы и молекулы растворителя разнополярны, то между коллоидными частицами и дисперсионной средой отсутствует взаимодействие, значит отсутствуют и сольватные оболочки, либо образуются тонкие сольватные оболочки. Такие системы были названы лиофобными коллоидными растворами (от гр.lyo жидкость + phobos боязнь). В случае, когда дисперсионной средой является вода, эти системы называются соответственно, гидрофильными и гидрофобными.
К лиофобным системам относятся типичные коллоидные системы, образо-ванные трудно растворимыми в дисперсионной среде веществами (слабые осно-вания, некоторые соли, металлы, аэрозоли, пены).
Лиофильные системы не обладают всеми типичными коллигативными свойствами, они растворяются самопроизвольно, термодинамически устойчивы, образуют гомогенные растворы. Поэтому лиофильных систем в настоящее время выделяют как особые группы дисперсных систем – растворы высокомо-лекулярных веществ (белков, полисахаридов, нуклеиновых кислот) и мицелярные растворы ПАВ.
Классификация по взаимодействию между частицами дисперсной фазы
(по подвижности дисперсной фазы)
Р.Зигмонди дисперсные системы разделил на свободнодисперные и связнодисперсные. В свободнодисперсных системах (золях, эмульсиях) частицы не связаны друг с другом, свободно перемещаются в дисперсионной среде под действием броуновского движения или силы тяжести. Лиозоли обладают текучестью.
В связнодисперсных системах частицы взаимодействуют друг с другом, под действием физических сил образуют пространственные сетки, структуры, поэтому не могут перемещаться. Такая система не может течь. Их называют гелями и студнями. К ним относятся пасты, концентрированные эмульсии, суспензии, пены, порошки, кремы.
Лекция 2
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ и ОПТИЧЕСКИЕ СВОЙСТВА КОЛЛОИДНЫХ СИСТЕМ
Молекулярно-кинетические свойства коллоидных систем, как и истинных растворов обнаруживаются в таких явлениях, как броуновское движение, диф-фузия, осмотическое давление и они связаны движением дисперсных частиц. Поскольку коллоидные частицы участвуют в тепловом движении и подчиняются молекулярно-кинетическим законам обычных растворов, экспериментально можно определить размер, массу и концентрацию частиц дисперсной фазы.
Диффузия. Диффузия – это самопроизвольный необратимый процесс вырав-нивания концентрации частиц по всему объёму раствора или газа под влиянием теплового движения. Процесс диффузии идёт самопроизвольно, поскольку он сопровождается увеличением энтропии системы, так как по второму закону тер-модинамики, равномерное распределение вещества в системе отвечает наиболее вероятному её состоянию. Для описания диффузии в коллоидных системах более справедливо применение I закона Фика:
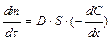 ,
,
где 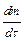 - масса вещества, диффундированного за единицу времени;
- масса вещества, диффундированного за единицу времени; 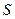 - пло-щадь диффузии,
- пло-щадь диффузии, 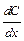 - градиент концентрации (знак «-» означает, что диффузия идёт в сторону уменьшения концентрации);
- градиент концентрации (знак «-» означает, что диффузия идёт в сторону уменьшения концентрации); 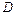 – коэффициент диффузии; это масса вещества, продиффундированного за единицу времени через единицу площади при градиенте концентрации, равном единице
– коэффициент диффузии; это масса вещества, продиффундированного за единицу времени через единицу площади при градиенте концентрации, равном единице 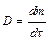 , т.е. масса вещества диффундирущего за единицу времени через поперечное сечение в 1 м2 при
, т.е. масса вещества диффундирущего за единицу времени через поперечное сечение в 1 м2 при 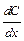 = 1 (физический смысл коэффициента диффузии).
= 1 (физический смысл коэффициента диффузии).
Эйнштейн показал, что коэффициент диффузии связан с размерами частиц, вязкости дисперсионной среды, температуры: 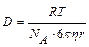 , м2/с. Как видно из формулы, чем меньше размер частиц, тем больше коэффициент диффузии. Для коллоидных систем D ~ 10-13 м2/с.
, м2/с. Как видно из формулы, чем меньше размер частиц, тем больше коэффициент диффузии. Для коллоидных систем D ~ 10-13 м2/с.
Так как в коллоидных системах размер частиц дисперсной фазы значительно больше размера молекул или ионов, скорость диффузии в коллоидных системах в целом небольшая, т.е. меньше скорости диффузии в истинных растворах.
Используя уравнение Эйнштейна можно определить размер частиц золей и молекулярную массу полимера. Для этого требуется экспериментально опреде-лить D. С этой целью, сначала оптическими методами, измеряя показатель пре-ломления или оптическую плотность раствора, измеряют скорость изменения концентрации в слое, а затем рассчитывают значение D.
В тех случаях, когда затруднено определение D через концентрацию, D и r частиц рассчитывают через смещение частиц.
После определения размера частиц можно рассчитать мицеллярную массу частиц или молекулярную массу полимера (что и было сделано впервые для белков). Для этого пользуются уравнением Перрена:
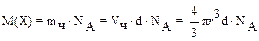 ,(а.е.м)
,(а.е.м)
где 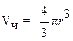 – объем одной частицы; d – плотность вещества.
– объем одной частицы; d – плотность вещества.
Броуновское движение
Историческая справка: Броуновское движение наблюдал Р.Браун под микроско-пом водной суспензии цветочной пыльцы в 1828 г. Оно количественно было исследовано в 1906 году французским ученым Ж.Перреном. На основе опытов он вычислил число Авогадро, за что получил Нобелевскую премию.
Броуновское движение проявляется в хаотическом и непрерывном движении частиц ДФ под действием ударов молекул дисперсионной среды, находящихся в состоянии интенсивного молекулярно-теплового движения. В зависимости от размера частиц их движение может иметь различные формы. Частицы коллоид-ных размеров под действием ударов молекул ДС с разных сторон, могут переме-щаться поступательно в разных направлениях. Траектория движения таких час-тиц представляет собой ломаную линию неопределенной конфигурации (рис.1).
 Рис.1 Схема броуновского движения одной частицы Рис.1 Схема броуновского движения одной частицы | Количественной мерой (интен-сивности броуновского движе-ния) принимают величину сред-него смешения (сдвига) частицы за определенный промежуток времени. Смещением частицы называют расстояние между проекциями начальной и конечной точек траектории на ось смещений. А.Эйнштейн и М.Смолуховский показали, что смещение части-цы не зависит от природы кол-лоидной системы, а определя-ется лишь размером частицы (r) и растет со временем (t). |
На него оказывают влияние температура (t) и вязкость среды (h):
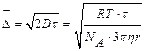 ,
,
где R – универсальная газовая постоянная, NA – число Авогадро,
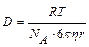 – коэффициент диффузии.
– коэффициент диффузии.
Как видно из уравнения, смещение частицы обратно пропорционально радиусу частицы. Это означает, что чем крупнее частица, тем меньше величина её смеще-ния. С увеличением размера частицы броуновское движение ослабевает и при каких-то размерах прекращается. Для частиц размером более 50 нм броуновское движение вообще не характерно. Броуновское движение наблюдают под микро-скопом или кинематографической микросъёмкой и используя уравнение рассчи-тывают размер коллоидных частиц.
Осмотическое давление коллоидных растворов. Осмос – сампроизвольный односторонний переход молекул дисперсионной среды через полупроницаемую мембрану из раствора с меньшей концентрацией в раствор с большей концентра-цией, т.е. односторонняя диффузия через полупроницаемую мембрану. За счет диффузии молекул дисперсионной среды через мембрану наблюдается увеличе-ние объёма раствора с большей концентрацией. Работа системы против внешнего давления (изменение объема раствора) описывается осмотическим давлением. Равновесное осмотическое давление растворов неэлектролитов рассчитывают по уравнению Вант-Гоффа: 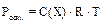 . Осмотическое давление – это свойство, определяемое числом частиц в растворе. Поэтому в случае коллоидных систем определяют по уравнению:
. Осмотическое давление – это свойство, определяемое числом частиц в растворе. Поэтому в случае коллоидных систем определяют по уравнению: 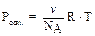 , где
, где 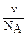 - численная (или частичная) концентрация. Численная концентрация представляет собой число частиц в 1 л дисперсной системы и её можно вычислить по соотношению
- численная (или частичная) концентрация. Численная концентрация представляет собой число частиц в 1 л дисперсной системы и её можно вычислить по соотношению 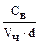 . Тогда
. Тогда 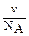 =
= 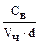 , а
, а 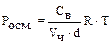 .
.
Как видно из уравнения, осмотическое давление пропорционально числу час-тиц в единице объема системы и не зависит от природы и массы частиц. Коллоидные растворы разных веществ с одинаковой численной концентрацией молекул или частиц оказывают одинаковое осмотическое давление. Например, при 273К при 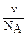 = 1 моль/л Росм. = 2,27.106 Па.
= 1 моль/л Росм. = 2,27.106 Па.
Осмотическое давление дисперсных систем отличается от осмотического давления истинных растворов:
-осмотическое давление коллоидных систем меньше осмотического давления истинных растворов, т.к. из-за низкой агрегативной устойчивости и больших размеров частиц, численная концентрация их обычно на 5 -7 порядков меньше, чем в истинных растворах при одинаковой молярной концентрации. Из-за малой величины осмотическое давление коллоидных растворов трудно измерить.
- в связи с термодинамической неустойчивостью в коллоидных растворах непрерывно протекают процессы агрегации и дезагрегации, что приводит к непостоянству осмотического давления во времени.
Все перечисленные особенности коллоидных растворов являются препятствием для применения осмотического давления при определении размеров частиц.
В отличие от лиофобных коллоидов, растворы ВМС (лиофильные коллоиды) при сравнительно небольших концентрациях показывают измеримые величины осмотического давления. Это позволяет использовать явление осмоса для определения молекулярной массы белков, полисахаридов и др. полимеров.
Лекция 2
Тема: Оптические свойства дисперсных систем.
Рассеивание света. При прохождении через молекулярную дисперсную систему (через истинные растворы) свет может только преломляться и погло-щаться. При прохождении через дисперсную систему возможно преломление, поглощение, отражение и рассеивание света, что обусловлено их дисперсностью, влиянием структуры, размера и формы частиц дисперсной фазы. Преобладание какого-либо из этих явлений зависит от соотношения длины волны падающего света и размера частиц ДФ. В микрогетерогенных системах размер частиц намного больше длины волны видимой части спектра. Поэтому свет отражается от поверхности частиц. В коллоидных растворах величина частиц 2 раза меньше длины волны видимого света: r ~ 0,5l. Поэтому в этом случае наблюдается рассеивание света. Сущность рассеивания света в дисперсной системе состоит в том, что луч света, встречая на своем пути частицу, как бы огибает её и несколько меняет свое направление. Это происходит по тому, что лучи длиннее размеров частиц и частицы удалены друг от друга на расстояния, больше длин волн. В коллоидных растворах рассеивание света проявляется в виде опалесценции – изменения окраски золя при рассматривании его в проходящем и отраженном свете. При рассмотрении золя в отраженном свете (при боковом освещении) на темном фоне всего проявляется матовое (чаще всего голубоватое) свечение. Если золь рассматривать в прямом проходящем свете, он может иметь красновато-желтую окраску.
Эффект Фарадея-Тиндаля: С опалесценцией, т.е. дифракцией света в микронеоднородной среде связана специфичная для коллоидных растворах явление – конус или эффект Фарадея-Тиндаля (1896 г.). Световая волна взаимо-
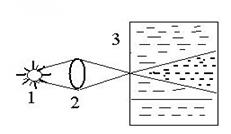 Рис.1. Конус Фарадея-Тиндаля: 1- источник света; 2 – линза; 3 – сосуд с коллоидным раствором. Рис.1. Конус Фарадея-Тиндаля: 1- источник света; 2 – линза; 3 – сосуд с коллоидным раствором. | действует не только с освещаемой, но и с «затемненной» стороны. Каждая частица частично переизлучает свет, вследствие чего при рассматривании с боку, наблюдается конусовидное рассеяние света. При тех же условиях молекулярно-дисперсные и микрогетерогенные системы не дают такого эффекта. Таким путем можно распознать коллоидные растворы. |
Интенсивность светорассеяния. Закон Рэлея: Интенсивность светорассеяния зависит от величины частиц, их концентрации, длины волны освещающего света, показателей преломления дисперсной фазы и дисперсионной среды. Такая зависимость для сферических частиц определяется уравнением Рэлея, называемым законом светорассеяния: 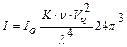 , где
, где
I - интенсивность рассеивания света; Io – интенсивность падающего (освещающего) света; 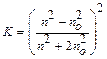 - коэффициент, зависящий от показателей преломления дисперсионной среды и дисперсной фазы; v – численная концентрация (1/м3); Vч – средний объем частицы (м3); l - длина световой волны.
- коэффициент, зависящий от показателей преломления дисперсионной среды и дисперсной фазы; v – численная концентрация (1/м3); Vч – средний объем частицы (м3); l - длина световой волны.
Как видно из уравнения, чем меньше длина световой волны, тем интенсивнее рассеивается свет в коллоидных растворах. Максимальное светорассеяние наблюдается в коллоидных растворах. С уменьшением или увеличением размера частиц, по сравнению с коллоидными частицами, интенсивность светорассеяния ослабевает пропорционально квадрату объема частиц. При размерах частиц более 0,1l свет отражается, в в растворах проявляется мутность, а опалесценция исчезает.
Спектр видимого света
| фиолетовая | синяя | зеленая | желтая | оранжевая | красная |
| 380− | 490− | 560− | 580− | 620− | 760− |
Если сравнивать спектр видимого света и уравнение Рэлея, видно, что максимальное светорассеяние будет наблюдаться в случае лучей фиолетового и синего света и минимальное – при красном свете. Этим объясняется цвет неба, морской воды, разведенного водой молока, гидрозолей канифоли, серы. Голубой цвет неба днем обусловлен рассеиванием коротких волн атмосферой Земли (наблюдение сбоку). Оранжевый или красный цвет неба при восходе и закате объясняется прохождением красного света через атмосферу. На этом основано и применение синего света для светомаскировки, красного – для сигнализации (красный свет мало рассеивается, он виден в тумане и издалека).
Явление светорассеяния используется для количественных оптических методов исследования, в частности для определения объема и размера частиц при известной концентрации или концентрации вещества. Для этих целей применяют специальные приборы: нефелометры, тиндалиметры, ультрамикроскопы.
Нефелометрия:оптический метод анализа, который заключается в измерении интенсивности света, рассеянного дисперсной системой. На практике при относительных измерениях сравнивают опалесценцию исследуемого раствора с опалесценцией стандартного раствора, размер частиц которого известен. При одинаковой объемной концентрации дисперсной фазы в обоих растворах интенсивности светорассеяний будут пропорциональны объемам или кубов диаметров частиц: 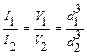 . Для проведения измерений применяют визуальные нефелометры, калориметры. Нефелометр (рис.2) состоит из 2-х одинаковых цилиндрических кювет, налитых исследуемым и стандартным растворами, источника света, регистрирующего прибора (окуляра). Освещенность растворов (высоту освещенного столба жидкости) можно регулировать поднятием или опусканием специальных экранов. Свет, попадая на жидкости, рассеивается.
. Для проведения измерений применяют визуальные нефелометры, калориметры. Нефелометр (рис.2) состоит из 2-х одинаковых цилиндрических кювет, налитых исследуемым и стандартным растворами, источника света, регистрирующего прибора (окуляра). Освещенность растворов (высоту освещенного столба жидкости) можно регулировать поднятием или опусканием специальных экранов. Свет, попадая на жидкости, рассеивается.
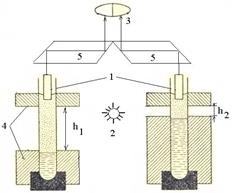 Рис.2. Схема нефелометра:1- кюветы(пробирки) с растворами; 2 –источник освещения; 3 – окуляр; 4 – подвижные экраны; 5 – оптическая часть прибора. Рис.2. Схема нефелометра:1- кюветы(пробирки) с растворами; 2 –источник освещения; 3 – окуляр; 4 – подвижные экраны; 5 – оптическая часть прибора. | При работе с нефелометром добиваются одинаковой освещенности полукругов окуляра. Так как интенсивность света, рассеянного каждой кюветой пропорциональна высоте её освещенной части, справедливо соотношение: 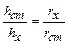 . Отсюда, . Отсюда, 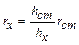 . Нефелометрия используется для установления формы и размера частиц, степени их дисперсности, молекулярной массы ВМС (белков, нуклеиновых кислот и др.), строения и конфигурации макромолекул. . Нефелометрия используется для установления формы и размера частиц, степени их дисперсности, молекулярной массы ВМС (белков, нуклеиновых кислот и др.), строения и конфигурации макромолекул. |
Ультрамикроскопия (разработана в 1903 году Зигмонди и Зидентопф). Принцип метода состоит в том, что используя обычный оптический микроскоп, изменяют способ освещения объекта. Вместо проходящего света применяют боковое освещение мощным пучком света. При таких условиях частицы ДФ кажутся светящимися точками на темном фоне. Их видны, даже, если размер частиц меньше разрешающей способности микроскопа, т.к. каждая частица
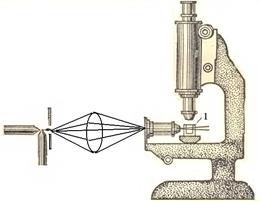 Рис.3. Схема ультрамикроскопа:1- кювета с исследуемым золем Рис.3. Схема ультрамикроскопа:1- кювета с исследуемым золем | 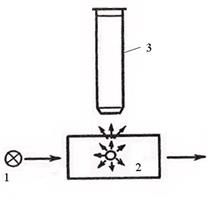 Рис.4. Схема ультрамикроскопа: 1 – источник света; 2 – коллоидный раствор; 3 – тубус микроскопа. Рис.4. Схема ультрамикроскопа: 1 – источник света; 2 – коллоидный раствор; 3 – тубус микроскопа. |
испускает рассеянный свет. Ультрамикроскопией можно подсчитать число частиц диаметром более 2-3 нм. Для этого в окуляре микроскопа имеется сетка, разделенная на квадраты. Подсчет частиц ведут поочередно в одном из центральных квадратов, где наблюдается наиболее интенсивное освещение. Форму частиц устанавливают по характеру их свечения. Если рассеянный свет испускается ровно, без мигания, то частицы – сферические. Частицы пластинчатой или палочкообразной формы под действием броуновского движения меняют свое положение. Поэтому в таких системах наблюдается мерцание (исчезновение и появление свечения). С помощью ультрамикроскопии можно вычислить число частиц в пробе и их размер, условно приняв для частиц сферическую или кубическую форму. Для этого необходимо знать общую массу частиц в пробе и их плотность. Предварительно рассчитав весовую и частичную концентрации или зная объем золя и подсчитав число частиц в нем, можно вычислить размер частиц: 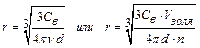 .
.
В настоящее время применяются и электронные микроскопы ( в них вместо световых лучей используется пучок электронов). У них разрешающая способность может достичь 0,15 – 0,2 нм, тогда как для светового микроскопа – 225 нм. Электронный микроскоп позволяет увидеть отдельные коллоидные частицы, крупные макромолекулы белков и вирусов, их структуру. Однако, электронный микроскоп не позволяет наблюдать систему в динамических условиях, т.к. объект рассматривается в виде реплик (отпечатков).
Лекция № 3
