Основные физические величины и законы. Мощность (поток) теплового излучения

Мощность (поток) теплового излучения

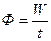(Вт),

где 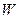– энергия всех длин волн, излученных телом за время .

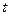Энергетическая светимость тела

( ),

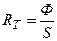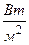где 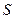– площадь излучающей поверхности тела.

Спектральная плотность энергетической светимости (излучательная способность)

,

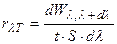где 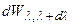– энергия излучения в интервале длин волн от 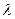до .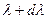

Закон Стефана-Больцмана

,

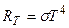где 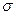– постоянная Стефана-Больцмана; 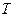– температура абсолютно черного тела (а.ч.т.).

Закон смещения Вина

,

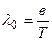где 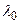– длина волны, соответствующая максимуму спектральной плотности энергетической светимости а.ч.т.; 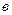– постоянная Вина.

Энергия фотона

,

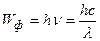где 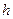– постоянная Планка; 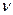– частота волны.

Формула Планка

.

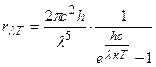Уравнение Эйнштейна для внешнего фотоэффекта

,

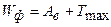где 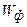– энергия фотона, падающего на металл; 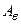– работа выхода электрона из металла; 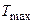– максимальная кинетическая энергия фотоэлектрона.

«Красная граница» фотоэффекта для данного металла

; .

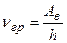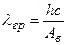Учитывая взаимосвязь массы и энергии 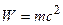, находим массу и импульс фотона

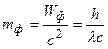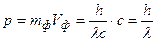; ; так как .

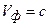Изменение длины волны рентгеновского излучения при комптоновском рассеянии

,

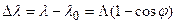где 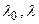– длины волн падающего и рассеянного излучения; 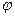– угол рассеяния; 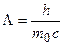– комптоновская длина волны. При рассеянии на электронах .

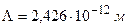Пример 1. От двух S₁ и S₂ когерентных источников ( 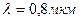) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку ( 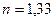), интерференционная картина изменилась на противоположную. При какой наименьшей толщине 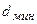пленки это возможно?

Дано: ; .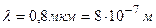

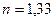Найти: .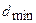

Решение. Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода лучей на нечетное число половин длин волн, т. е.

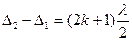, (1)

где Δ₁ — оптическая разность хода лучей до внесения пленки; Δ₂ — оптическая разность хода тех же лучей после внесения пленки; k = 0, ±1, ±2, ... .

Наименьшей толщине d_min пленки соответствует k = 0. При этом формула (1) примет вид

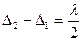. (2)

Выразим оптические разности хода Δ₂ и Δ₁. Из рисунка 20 cледует:

,

.

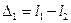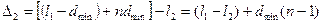Подставим выражения Δ₁ и Δ₂ в формулу (2):

,

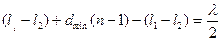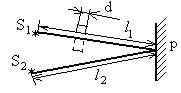или .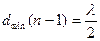

Отсюда получим .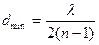

Подставив сюда числовые значения, найдем

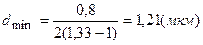. Рисунок 20.

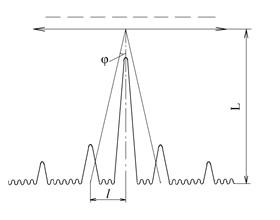
Пример 2.На дифракционную решетку нормально к ее поверхности падает свет с длиной волны 550 нм. На экран, находящийся от решетки на расстоянии 1 м, с помощью линзы, расположенной вблизи решетки, проецируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии 12 см от центрального.

Определить: 1) период решетки; 2) число штрихов на 1 см ее длины; 3) общее число максимумов, даваемых решеткой; 4) угол дифракции, соответствующий последнему максимуму.

Дано: ; ; ; ; .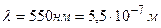

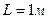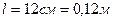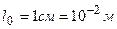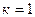Определить: , , , .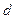

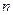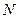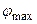Рисунок 21.

Решение. 1) Из условия главных максимумов

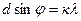. (2.1)

Находим период решетки

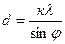. (2.2)

Из рисунка 21 следует

.

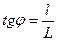Так как 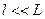, то .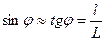

Тогда выражение (2.2) примет вид

.

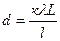Подставим численные значения

.

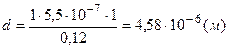2) число штрихов «n» на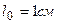

.

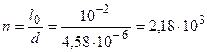3) Поскольку наибольший угол отклонения лучей решетки не может быть более 90⁰ , из условия (2.1) можно найти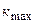

.

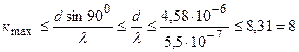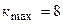, так как число 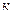должно быть целым.

Общее число максимумов, даваемых дифракционной решеткой

.

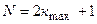Так как максимумы наблюдаются как справа, так и слева от центрального максимума (единица учитывает центральный максимум)

.

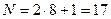4) Угол дифракции, соответствующий последнему максимуму, найдем, записав условие (2.1) в виде

.

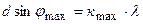Откуда

.

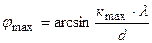Подставляя численные значения, получим

.

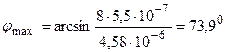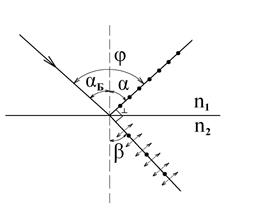Пример 3. Естественный луч света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины луч повернут на угол 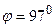по отношению к падающему лучу (рисунок 22).

Рисунок 22.

Определить показатель преломления жидкости, если отраженный свет максимально поляризован.

Дано: ; ; .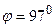

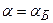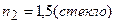Найти: .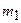

Решение. Согласно закону Брюстера луч света, отраженный от диэлектрика, максимально поляризован в том случае, если

.

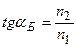Согласно условию задачи отраженный луч повернут на угол 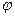относительно падающего луча. Так как угол падения равен углу отражения, то

.

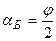Получаем .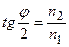

Отсюда .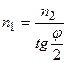

Сделав подстановку числовых значений, получим

.

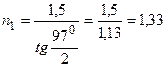Пример 4. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны 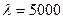Å. Принимая Солнце за абсолютно черное тело, определить:

1) температуру поверхности Солнца;

2) энергетическую светимость Солнца;

3) поток энергии, излучаемый Солнцем;

4) массу электромагнитных волн (всех длин), излучаемых Солнцем за одну секунду.

Дано: 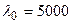Å ; ; ; ;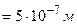

.

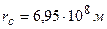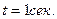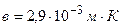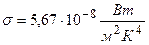Найти: , , , .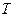

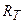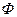
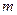Решение.

1. Температуру поверхности Солнца найдем из закона смещения Вина

.

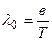Отсюда .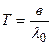

.

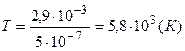2. Энергетическая светимость 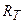абсолютно черного тела выражается законом Стефана-Больцмана

.

.

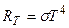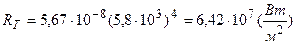3. Поток энергии 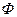, излучаемый Солнцем равен

,

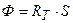где 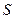– площадь поверхности Солнца

,

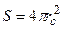где 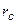– радиус Солнца.

Таким образом, получаем

.

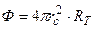Подставим числовые значения

.

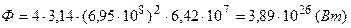4. Массу электромагнитных волн (всех длин) определим, применив закон

.

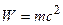Энергия электромагнитных волн 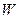равна

.

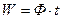Следовательно,

.

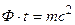Отсюда

.

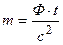Подставляя численные значения, находим

.

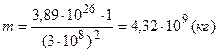Пример 5. Определить постоянную Планка 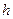, если известно, что фотоэлектроны, вырываемые с поверхности металла светом с частотой 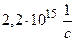, полностью задерживаются обратным потенциалом 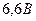, а вырываемые светом с частотой 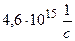– потенциалом .

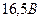Дано: ; ;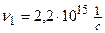

; ;

.

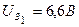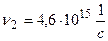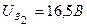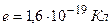Найти: .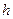

Решение. Фотоэлектроны задерживаются электрическим полем, если работа электрического поля по их торможению

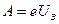
будет равна (или больше) максимальной кинетической энергии этих фотоэлектронов при их вылете из металла

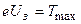. (5.1)

Тогда формула Эйнштейна для фотоэффекта

.

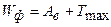С учетом формул 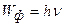и (5.1) уравнение примет вид

.

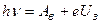Применяя эту формулу для каждого из указанных в условиях случаев, получаем систему двух уравнений

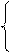
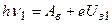
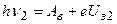
Откуда

.

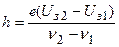Подставляя заданные численные значения величин, получим

.

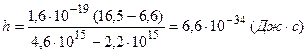Пример 6. Определить энергию и импульс электрона отдачи при эффекте Комптона, если фотон ( 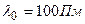) был рассеян на угол .

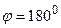Дано: ; ; .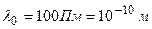

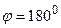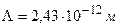Найти: , .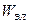

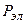Решение. Энергия электрона отдачи равна разности энергий падающего и рассеянного фотонов

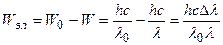. (6.1)

По формуле Комптона

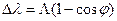. (6.2)

Подставив уравнение (6.2) в формулу (6.1) и учитывая, что 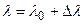, найдем

.

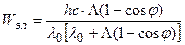Подставляя численные значения величин, получим

.

.

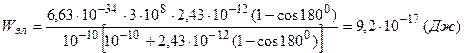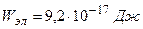По закону сохранения импульса имеем

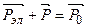, (6.3)

где 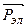– импульс электрона отдачи, 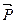– импульс рассеянного фотона, 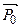– импульс падающего фотона.

Учитывая условие задачи 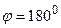, запишем уравнение (6.3) в скалярном виде

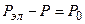
или 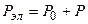. (6.4)

Импульсы падающего и рассеянного фотонов равны

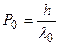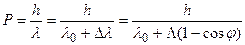; . (6.5)

Подставляя выражения (6.5) в уравнение (6.4) , получаем

.

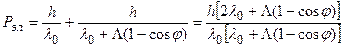Подставим численные значения

.

.

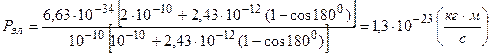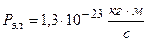Задачи

5.01. На тонкую глицериновую пленку толщиной 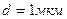, нормально к ее поверхности падает белый свет. Определить длины волн λ лучей видимого участка спектра ( 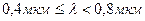), которые будут ослаблены в результате интерференции.

5.02. На стеклянную пластинку нанесен тонкий слой прозрачного вещества с показателем преломления 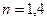. Пластинка освещается пучком параллельных лучей длиной волны 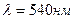, падающих на пластинку нормально. Какую минимальную толщину 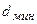должен иметь слой, чтобы отраженные лучи имели наименьшую яркость?

5.03. Расстояние L от щелей до экрана в опыте Юнга равно 1,5 м. Определить расстояние d между щелями, если на отрезке длиной 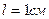укладывается 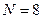темных интерференционных полос. Длина волны .

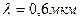5.04. На мыльную пленку в направлении нормали к ее поверхности падает монохроматический свет длиной волны 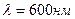. Отраженный от пленки свет максимально усилен вследствие интерференции. Определить минимальную толщину 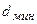пленки. Показатель преломления мыльной воды .

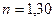5.05. На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещается монохроматическим светом длиной волны 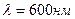. Найти радиус R линзы, если радиус восьмого темного кольца Ньютона в отраженном свете .

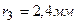5.06. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления п жидкости, если радиус 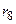восьмого темного кольца Ньютона при наблюдении в отраженном свете длиной волны 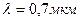равен 2 мм. Радиус кривизны линзы .

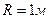5.07. Плосковыпуклая линза с фокусным расстоянием 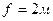лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете 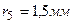. Определить длину световой волны λ.

5.08. На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в

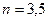раза больше длины световой волны. Найти общее число М дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.

5.09. На дифракционную решетку падает нормально параллельный пучок лучей белого света. Спектры второго и третьего порядка частично накладываются друг на друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница ( 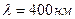) спектра третьего порядка?

5.10. Постоянная дифракционной решетки в 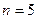раз больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол α между двумя первыми симметричными дифракционными максимумами.

5.11. На дифракционную решетку, содержащую 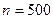штрихов на миллиметр, падает нормально белый свет. Спектр проектируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана 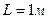. Границы видимого спектра: , .

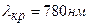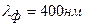5.12. Расстояние между штрихами дифракционной решетки 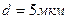. На решетку падает нормально свет с длиной волны 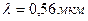. Максимум какого наибольшего порядка дает эта решетка?

5.13. На дифракционную решетку нормально падает пучок света. Угол дифракции для натриевой линии ( 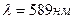) в спектре первого порядка был найден равным 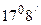. Некоторая линия дает в спектре второго порядка угол дифракции 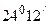. Найти длину волны этой линии и число штрихов на 1 мм решетки.

5.14. Луч света, идущий в стеклянном сосуде с водой, отражается от дна сосуда. При каком угле i₁ падения отраженный луч максимально поляризован?

5.15. Угол α между плоскостями поляризаторов (поляроидов) равен 60⁰. Естественный свет, проходя через такую систему, ослабляется в 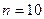раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах.

5.16. Между скрещенными николями поместили пластинку кварца толщиной 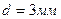, в результате чего поле зрения поляриметра стало максимально светлым. Определить постоянную вращения α кварца для монохроматического света, использованного в опыте.

5.17. Луч света переходит из воды в стекло так, что луч, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол γ между падающим и преломленным лучами.

5.18. Луч света последовательно проходит через два николя, главные плоскости которых образуют между собой угол 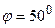. Принимая, что коэффициент поглощения k каждого николя равен 0,1 найти, во сколько раз луч, выходящий из второго николя, ослаблен по сравнению с лучом, падающим на первый николь.

5.19. Угол падения луча на поверхность жидкости 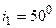. Отраженный луч максимально поляризован. Определить угол 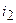преломления луча.

5.20. Пластинку кварца толщиной 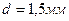поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол 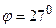. Какой наименьшей толщины 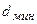следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным?

5.21. Определить температуру Т и энергетическую светимость 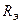абсолютно черного тела, если максимум энергии излучения приходится на длину волны .

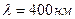5.22. Поток излучения абсолютно черного тела 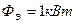, максимум энергии излучения приходится на длину волны 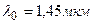. Определить площадь 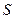излучающей поверхности.

5.23. Поверхность тела нагрета до температуры 1000 К. Затем одна половина этой поверхности нагревается на 100 К, другая охлаждается на 100 К. Во сколько раз изменится энергетическая светимость поверхности этого тела?

5.24. Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра ( 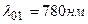) на фиолетовую ( )?

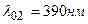5.25. Какое количество энергии излучает 1 см² затвердевающего свинца в 1 с? Отношение энергетических светимостей поверхности свинца и абсолютно черного тела для этой температуры считать равным 0,6.

5.26. Абсолютно черное тело находится при температуре 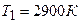. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 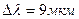. До какой температуры 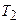охладилось тело?

5.27. Из смотрового окошечка печи излучается поток 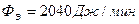. Определить температуру Т печи, если площадь отверстия .

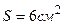5.28. Абсолютно черное тело имеет температуру 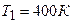. Какова будет температура Т₂ тела, если в результате нагревания поток излучения увеличится в 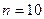раз?

5.29. Мощность излучения абсолютно черного тела равна 10 кВт. Найти площадь излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум спектральной плотности его энергетической светимости, равна 700 нм.

5.30. Мощность излучения абсолютно черного тела равна 34 кВт. Найти температуру этого тела, если известно, что поверхность его равна 0,6 м².

5.31. Красная граница фотоэффекта для цезия 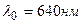. Определить максимальную кинетическую энергию Т фотоэлектронов в электрон-вольтах, если на цезий падают лучи с длиной волны .

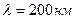5.32. На фотоэлемент с катодом из рубидия падают лучи с длиной волны 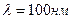. Найти наименьшее значение задерживающей разности потенциалов 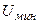, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.

5.33. На поверхность металла падают монохроматические лучи с длиной волны 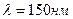. Красная граница фотоэффекта 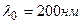. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?

5.34. Фотон с энергией 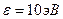падает на цинковую пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластины.

5.35. На металлическую пластину направлен пучок ультрафиолетовых лучей ( 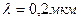). Фототок прекращается при минимальной задерживающей разности потенциалов 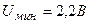. Определить работу выхода А электронов из металла.

5.36. Рентгеновские лучи ( 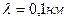) рассеиваются электронами, которые можно считать практически свободными. Определить максимальную длину волны 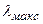рентгеновских лучей в рассеянном пучке.

5.37. Определить угол 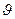, на который был рассеян 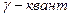с энергией 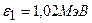при эффекте Комптона, если кинетическая энергия электрона отдачи .

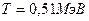5.38. В результате эффекта Комптона на свободных электронах фотон с энергией 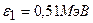был рассеян на угол 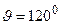. Определить энергию 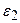рассеянного фотона.

5.39. Фотон сэнергией 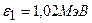был рассеян при эффекте Комптона на свободном электроне на угол 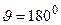. Определить кинетическую энергию Т электрона отдачи.

5.40. Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол 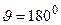? Энергия фотона до рассеяния .

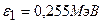ФИЗИКА АТОМА И ОСНОВЫ ФИЗИКИ ЯДРА