Примесная электропроводность

полупроводников

где е – элементарный заряд,

n_- и n₊ - концентрация электронов

и дырок,

b_- и b₊ - подвижность электронов

и дырок.

Примеры решения задач

1. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить дебройлевскую длину волны протона.

Дано: Т = Е₀/4, Е₀ = 1,50 ∙ 10^-10 Дж.

Найти: λ.

Решение. Длина волны де Бройля λ определяется по формуле

(1)

где h – постоянная Планка, р – импульс частицы.

Так как по условию задачи

Т = Е₀/4, (2)

кинетическая энергия Т протона сравнима с его энергией покоя Е₀, импульс р и кинетическая энергия связаны релятивистским соотношением

(3)

где с – скорость света в вакууме. Подставляя в (3) условие (2), найдем

(4)

Учитывая равенство (4), запишем (1) в виде

(5)

Подставляя в (5) числовые значения, получим

Ответ: λ = 1,77 ∙ 10^-15 м.

2.Масса движущегося электрона в три раза больше его массы покоя. Чему равна минимальная неопределенность координаты электрона?

Дано: m = 3m₀; m₀ = 0,91 ∙ 10^-30 кг.

Найти: Δх_min.

Решение. Согласно соотношению неопределенностей Гейзенберга,

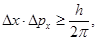(1)

где Δх и Δр_х – неопределенности координаты и импульса частицы, h – постоянная Планка.

Учитывая, что

(2)

где m – масса, v – скорость частицы, соотношение (1) можно представить в виде

(3)

Поскольку неопределенность скорости v_х, как и сама скорость, не может превышать скорость света с в вакууме, то

(4)

Согласно условию

m = 3m₀. (5)

Подставляя в (4) условие (5), получим

(6)

Проводя вычисления, найдем

Ответ: Δх_min = 1,28 ∙ 10^-13 м.

3. Среднее время жизни возбужденных состояний атома составляет 10 нс. Вычислить естественную ширину спектральной линии (λ = 0,7 мкм), соответствующую переходу между возбужденными уровнями атома.

Дано: τ = 10^-8 с; λ = 7 ∙ 10^-7 м.

Найти: Δλ_min.

Решение. При переходе электрона из одного стационарного состояния в другое излучается (или поглощается) энергия, равная

(1)

где Е_п и Е_к – энергетические уровни атома, λ – длина волны излучения, с – скорость света в вакууме, h – постоянная Планка.

Из (1) следует, что неопределенность длины волны Δλ излучения связана с неопределенностью энергии уровней ΔЕ_п и ΔЕ_к атома соотношением

(2)

Согласно соотношению неопределенностей Гейзенберга,

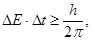(3)

где Δt – неопределенность момента времени перехода атома из одного стационарного состояния в другое.

Поскольку Δt не превышает среднее время жизни τ возбужденного состояния атома, минимальная неопределенность энергии возбужденных уровней, согласно (3), равна

(4)

Из (2) с учетом (4) найдем минимальную неопределенность длины волны излучения, которая называется естественной шириной спектральной линии

(5)

Если одно из состояний, между которыми совершается переход, является основным, то

(6)

поскольку для основного состояния τ = ∞. Для возбужденных состояний с одинаковым временем жизни τ_п = τ_к = τ имеем

(7)

Подставляя в (7) числовые значения, получим

Ответ: Δλ_min = 5,2 ∙ 10^-14 м.

4. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности.

Дано: l, w_п = w_∞, n = 2.

Найти: х.

Решение. Волновая функция ψ, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид

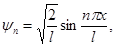(1)

где n – номер энергетического уровня (n = 1, 2, 3, …), х – координата частицы в яме (0 ≤ х ≤ l).

Согласно физическому смыслу волновой функции,

(2)

где w – плотность вероятности обнаружения частицыв точке с координатой x.

Если частица находится на втором энергетическом уровне (n = 2), то

(3)

В соответствии с принципом соответствия Бора, выражение для классической плотности вероятности получается при n → ∞

(4)

Приравнивая по условию задачи выражение (3) к (4), получим

(5)

Решая уравнение (5), найдем

. (6)

В пределах ямы (0 ≤ х ≤ l) таких точек четыре:

Ответ:

5. Длина волны линии L_a вольфрама равна 0,148 нм. Найти постоянную экранирования.

Дано: λ = 1,48 ∙ 10^-10 м.

Найти: а.

Решение. В соответствии с законом Мозли

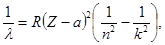(1)

где R – постоянная Ридберга; Z – порядковый номер элемента (для вольфрама Z = 74); а – постоянная экранирования; n – номер энергетического уровня, на который переходит электрон (для L – серии n = 2), k - номер энергетического уровня, с которого переходит электрон (для L_a – линии k = 3).

Из (1) находим

(2)

Подставляя числовые данные, получаем

Ответ: а = 7,4.

6. Вычислить дефект массы, энергию связи и удельную энергию связи ядра

Решение. Дефект массы Δm ядра определяется по формуле

(1)

где Z – зарядовое число, A – массовое число, m_p – масса протона, m_n – масса нейтрона, m_я – масса ядра.

Формулу (1) можно также записать в виде

(2)

где - масса атома 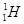, m_a – масса атома, дефект массы ядра которого определяется.

Из справочных таблиц находим:

а. е. м.; m_n = 1,00867 а. е. м.; = 15,99492 а. е. м.

Подставляя в (2) числовые данные (для числа Z = 8 и A = 16), получим

Δm = 0,13708 а. е. м.

Энергия связи ядра Е_св определяется по формуле

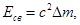(3)

где с – скорость света в вакууме.

Если дефект массы Δm выражать в а. е. м., а энергию связи Е_св - в МэВ, то формула (3) принимает вид

(4)

Подставляя в (4) числовые значения, получим

Удельная энергия связи ε_св вычисляется по формуле

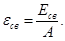(5)

Проводя вычисления, получим

Ответ: Δm = 0,13708 а. е. м.; Е_св = 128 МэВ; ε_св = 8 МэВ.

7. Сколько атомов распадается в 1г трития за среднее время жизни этого изотопа.

Дано: m = 10^-3 кг; t = τ.

Найти: N’.

Решение. Согласно закону радиоактивного распада

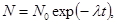(1)

где N – число не распавшихся атомов в момент времени t, N₀ – начальное число радиоактивных атомов в момент t = 0, λ – постоянная радиоактивного распада.

Среднее время жизни τ радиоактивного изотопа – величина, обратная постоянной распада,

(2)

По условию t = τ. Подставляя в (1) вместо t значение τ из (2), получим

(3)

Число атомов, распавшихся за время t = τ, равно

(4)

Найдем число атомов N₀, содержащихся в массе m = 1 г изотопа :

(5)

где М = 3 ∙ 10^-3 кг/моль – молярная масса изотопа , N_A – число Авогадро.

Учитывая (5), запишем выражение (4) в виде

(6)

Подставляя в (6) числовые значения, получим

Ответ: N’ = 1,27 ∙ 10²³.

8. На поверхность воды падает гамма – излучение с длиной волны 0,414 пм.На какой глубине интенсивность излучения уменьшится в два раза?

Дано: λ = 4,14 ∙ 10^-13 м; I₀/I = 2.

Найти: х.

Решение. Согласно закону поглощения гамма – излучения веществом

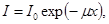(1)

где I₀ – интенсивность падающего излучения, I - интенсивность излучения на глубине х, μ – коэффициент линейного поглощения.

Решая уравнение (1) относительно х, найдем

(2)

Для определения коэффициента линейного ослабления вычислим энергию ε гамма – фотонов:

(3)

где λ – длина волны излучения, h – постоянная Планка, с – скорость света в вакууме.

Подставляя в (3) числовые значения, получим

По графику зависимости μ от ε (рис. 5) находим

μ = 0,04 см^-1.

Подставляя числовые значения в выражение (2), получим

Ответ: х = 17,3 см.

9. Вычислить энергию ядерной реакции

Выделяется или поглощается энергия при этой реакции?

Решение. Энергия ядерной реакции определяется по формуле

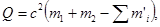(1)

где m₁ и m₂ – массы частиц, вступающих в реакцию; Σm’_i – сумма масс частиц, образовавшихся в результате реакции.

Если массу частиц выражать в а. е. м., а энергию реакции в МэВ, то формула (1) принимает вид

(2)

При вычислении энергии ядерной реакции можно использовать вместо масс их ядер массы атомов. Из справочных данных находим:

Дефект массы реакции равен

Подставляя значение дефекта массы реакции в (2), получим

Q = 931 МэВ/а. е. м. ∙ (- 0,01864 а. е. м) = - 17,3 МэВ.

Поскольку Q < 0, энергия в результате реакции поглощается.

Ответ: Q = - 17,3 МэВ.

10. Полоний имеет простую кубическую решетку. Постоянная решетки равна 0,334 нм. Вычислить плотность полония.

Дано: а = 3,34 ∙ 10^-10 м.

Найти: ρ.

Решение. Плотность полония можно вычислить по формуле

(1)

где m – масса атома полония, n – число атомов в единице объема.

Полоний имеет простую кубическую решетку. Некоторые характеристики кубических решеток приведены в следующей таблице.

	Тип решетки
ПК	ОЦК	ГЦК
Объем элементарной ячейки Число атомов на одну ячейку Расстояние между ближайшими соседними атомами	а3   а	а3	а3

Обозначение решеток: ПК – простая кубическая; ОЦК – объемоцентрированная кубическая; ГЦК – гранецентрированная кубическая.

Из таблицы следует, что для простой кубической решетки

(2)

где а – постоянная решетки.

Массу атома полония можно вычислить по формуле

(3)

где М – молярная масса полония, N_A – число Авогадро.

Подставляя (2) и (3) в (1), получим

(4)

Проводя вычисления, найдем

Ответ: ρ = 9,31 ∙ 10³ кг/м³.

11. Молярная изохорная теплоемкость аргона при температуре 4 К равна 0,174 Дж/(моль ∙ К). Определить значение молярной изохорной теплоемкости аргона при температуре 2 К.

Дано: Т₁ = 4 К; С₁ = 0,174 Дж/(моль∙ К); Т₂ = 2 К.

Найти: С₂.

Решение. Согласно теории Дебая, теплоемкость кристаллической решетки при низких температурах Т, когда Т << θ_D (квантовая область), где θ_D – характеристическая температура Дебая, пропорциональна кубу термодинамической температуры,

(1)

где С – молярная изохорная теплоемкость, R – молярная газовая постоянная.

При высоких температурах, когда Т >> θ_D (классическая область), теплоемкость кристаллической решетки описывается законом Дюлонга и Пти

(2)

Поскольку при Т₁ = 4 К теплоемкость аргона С₁ = 0,174 Дж/(моль∙ К) много меньше, чем выполняется закон Т³ Дебая, согласно которому

(3)

Отсюда

(4)

или

(5)

Подставляя в (5) числовые данные, получим

Ответ: С₂ = 0,022 Дж/(моль ∙ К).

12. Дебаевская температура кристалла равна 150 К. Определить

максимальную частоту колебаний кристаллической решетки. Сколько фононов

такой частоты возбуждается в среднем в кристалле при температуре 300К?

Дано: θ_D = 150 К; Т = 300К.

Найти: v_max, ‹N_i›.

Решение. Дебаевская температура

(1)

где v_max – максимальная частота колебаний кристаллической решетки, h – постоянная Планка, k – постоянная Больцмана.

Из (1) найдем

(2)

Подставляя в (2) числовые значения, получаем

Среднее число фононов с энергией ε_i:

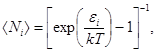(3)

где Т – термодинамическая температура кристалла.

Энергия фонона, соответствующая частоте колебания v_max,

(4)

Подставляя (4) в (3), находим

Ответ: v_max = 3,12 ∙ 10¹² Гц;‹N_i› = 1,54.