Молярную массу смеси газов найдем по формуле

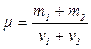(5)

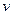где ₁ и 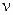₂ — число молей гелия и водорода соответственно. Число молей газов определим по формулам:

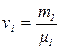(6)

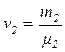(7)

Подставляя (6) и (7) в (5), найдем

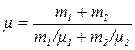(8)

Подставляя числовые значения в формулы (4) и (8), получаем:

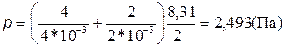
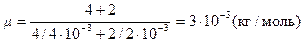
Ответ:p= 2493 кПа, 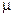=3 • 10^-3 кг/моль.

Задача 8. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К?

Решение. Считаем водород идеальным газом. Молекула водорода — двухатомная, связь между атомами считаем жесткой. Тогда число степеней свободы молекулы водорода равно 5. В среднем на одну степень свободы приходится энергия <E_i>=kТ/2 , где k—постоянная Больцмана; T—термодинами­ческая температура. Поступательному движению приписывается три (i=3), а вращательному две (i =2) степени свободы. Энергия одной молекулы

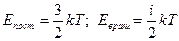
Число молекул, содержащихся в массе газа, равно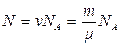

где v — число молей; N_A — постоянная Авогадро.

Тогда средняя кинетическая энергия поступательного движения молекул водорода

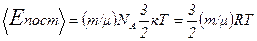(1)

где R=k • N_А - молярная газовая постоянная.

Средняя кинетическая энергия вращательногодвижения молекул водорода

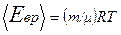. (2)

Подставляя числовые значения в формулы (1) и (2), имеем

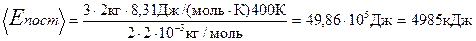
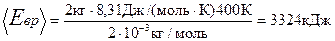
Ответ: <Е_пост>=4986кДж, <Е_вр>=2324кДж.

Задача 9. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27°С и давлении 100 кПа.

Решение. Средняя длина свободного пробега молекул кислорода вычисляется по формуле

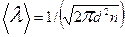(1)

где d — эффективный диаметр молекулы кислорода; п — число молекул в единице объема, которое можно определить из ура­внения

n=p/(kT), (2)

где k — постоянная Больцмана.

Подставляя(2) в (1), имеем

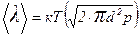(3)

Число соударенийZ, происходящих между всеми молекулами за 1 с, равно

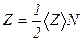(4)

где N — число молекул кислорода в сосуде объемом 2 • 10^-3 м³;

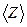— среднее число соударений одной молекулы за 1 с.

Число молекул в сосуде N=n • V. (5)

Среднее число соударений молекулы за 1 с равно

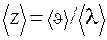(6)

где 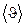— средняя арифметическая скорость молекулы

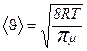(7)

Подставляя в (4) выражения (5), (6) и (7), находим

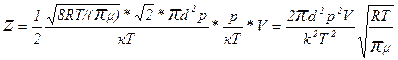
Подставляя числовые значения, получим

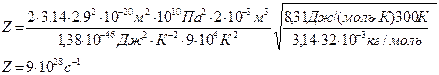
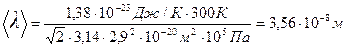
Ответ: Z=9 • 10²⁸ с-¹, < 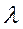>=3,56 • 10^-8 м.

Задача 10. Определить коэффициенты диффузии и внутреннего трения азота, находящегося при температуре Т=300 К и давлении 10⁵ Па.

Решение. Коэффициент диффузии определяется по формуле

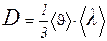(1)

где 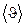— средняя арифметическая скорость молекул, равная

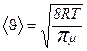(2)

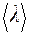— средняя длина свободного пробега молекул.

Для нахождения 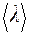воспользуемся формулой из решения примера 4

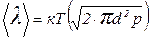(3)

Подставляя (2) и (3) в выражение (1), имеем

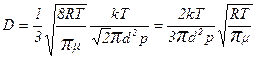(4)

Коэффициент внутреннего трения

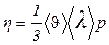(5)

где р - плотность газа при температуре 300 К и давлении 10⁵ Па. Для нахождения р воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота - при нормальных условиях Т_о=273 К, р= 1,01 • 10⁵ Па и в условиях задачи:

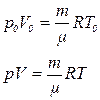(6)

Учитывая, что

,

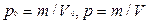имеем

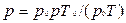. (7)

Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии (см. формулы (1) и (5)):

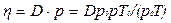
Подставляя числовые значения в (4) и (8), получим

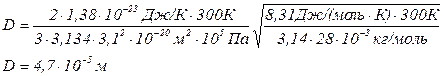
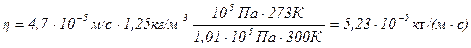
Ответ: D=4,7 10^-5м²/с,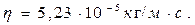

Задача 11. Объем аргона, находящегося при давлении 80кПа, увеличился от 1 до 2л. На сколько изменится внутренняя энергия газа, если расширение производилось: а) изобарно, б) адиабатно.

Решение. Применим первый закон термодинамики. Согласно этому закону, количество теплоты Q, переданное системе, расходуется на увеличение внутренней энергии 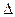U и на внешнюю механическую работу А:

Q= 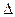U+А (1)

Величину 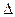U можно определить, зная массу газа m, удельную теплоемкость при постоянном объеме с_v и изменение температуры 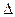Т:

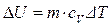(2)

Однако удобнее изменение внутренней энергии 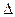U определять через молярную теплоемкость C_v, которая может быть выражена через число степеней свободы:

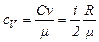(3)

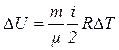(4)

Изменение внутренней энергии зависит от характера процесса, при котором идет расширение газа. При изобарном расширении газа, согласно первому закону термодинамики, часть количества теплоты идет на изменение внутренней энергии 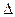U, которая выражается формулой (4) Найти 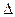U для аргона по формуле (4) нельзя, так как масса газа и температура в условии задачи не даны. Поэтому необходимо провести преобразование формулы (4).

Запишем уравнение Клапейрона - Менделеева для начального и конечного состояний газа:

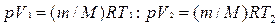(5)

или

p(V₂-V₁)=(m/M)R(T₂-Т₁).

Подставив (5) в формулу (4), получим

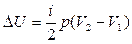(6)

Это уравнение является расчетным для определения 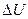при изобарном расширении.

При адиабатном расширении газа теплообмена с внешней средой не происходит, поэтому Q=0. Уравнение (1) запишется в виде

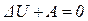(7)

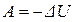(8)

Это соотношение устанавливает, что работа расширения газа может быть произведена только за счет уменьшения внутренней энергии газа (знак минус перед ):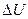

Формула работы для адиабатного процесса имеет вид

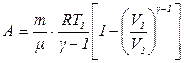(9)

где 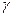- показатель степени адиабаты, равный отношению теплоемкостей: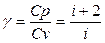

Для аргона - одноатомного газа (i=3) - имеем 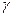=1,67.

Находим изменение внутренней энергии при адиабатном про­цессе для аргона, учитывая формулы (8) и (9):

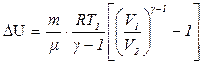(10)

Для определения работы расширения аргона формулу (10) следует преобразовать, учитывая при этом параметры, данные в условии задачи. Применив уравнение Клапейрона — Менделеева для данного случая 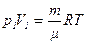, получим выражение для подсчета изменения внутренней энергии:

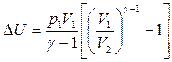(11)

Подставляя числовые значения в (6) и (11), имеем:

а) при изобарном расширении

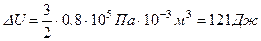
б) при адиабатном расширении

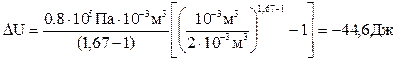
Ответ: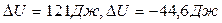

Задача 12.Заряд 15∙10^-9 Кл равномерно распределен по тонкому кольцу радиусом 0,2 м. Найдите напряженность электрического поля в точке, находящейся на оси кольца на расстоянии 15 см от его центра.

Решение. Разделим кольцо на одинаковые бесконечно малые участки dl. Заряд каждого участка dq можно считать точечным.

Напряженность электрического поля dE , создаваемого в точке А на оси кольца зарядом dq, равна:

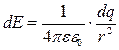(1)

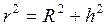где (2)

Полная напряженность поля Е в точке А, создаваемая зарядом q, согласно принципу суперпозиции равна векторной сумме напряженностей dE_i полей, создаваемых всеми точечными зарядами: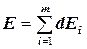

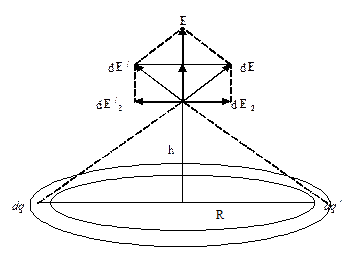
Вектор dE разложим на составляющие: вектор dE₁ (направлен вдоль оси кольца) и вектор dE₂ (параллелен плоскости кольца).

Тогда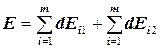

Для каждой пары зарядов dq и dq^/, расположенных симметрично относительно центра кольца, dE₂ и dE^/₂ в сумме дадут нуль, и значит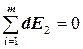

Составляющие dE₁ для всех элементов направлены одинаково вдоль кольца, поэтому полная напряженность в точке, лежащей на оси кольца, также направлена вдоль оси.

Модуль полной напряженности найдем интегрированием:

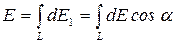(3)

где α-угол между вектором dE и осью кольца;

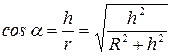(4)

Используя выражения (1), (2) и (4), для E получаем:

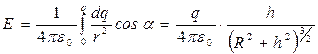
Подстановка числовых данных дает:

E=1,3∙10³В/м.

Ответ: E=1,3∙10³В/м.

Задача 13. Заряд переносится в воздухе из точки, находящейся на расстоянии 1м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?

Решение.Работа внешней силы по перемещению заряда q из точки поля с потенциалом φ_i в точку с потенциалом φ₀ равна

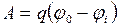(1)

Бесконечная равномерно заряженная нить с линейной плотностью заряда τ создает аксиально-симметричное поле напряженностью .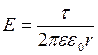

Напряженность и потенциал этого поля связаны соотношением

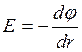, откуда .

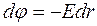Разность потенциалов точек поля на расстоянии r_i и r₀ от нити

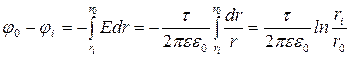
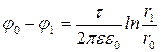
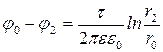(2)

Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:

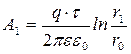
Подставив численные значения, получим:

A₁=4,1∙10^-5 (Дж).

Ответ: A₁=4,1∙10^-5 (Дж).

Задача 14. Сила тока в проводнике сопротивлением 20 Ом нарастает в течение времени 2 с по линейному закону от 0 до 6 А.. Определить теплоту Q₁, выделившуюся в этом проводнике за первую секунду, и Q₂ - за вторую, а также найти отношение Q₂/Q₁.

Решение.Закон Джоуля-Ленца в виде 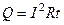справедлив для постоянного тока. Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде

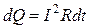(1)

Здесь сила тока является некоторой функцией времени.

В данном случае

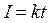, (2)

где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

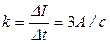
С учетом (2) формула (1) примет вид

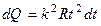(3)

Для определения теплоты, выделившейся за конечный интервал времени ∆t, выражение (3) надо проинтегрировать в пределах от t₁ до t₂:

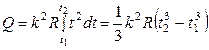
Произведем вычисления:

,

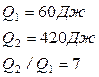т.е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.

Ответ: в 7 раз больше.

Задача 15. Электрическая цепь состоит из двух гальванически; элементов, трех сопротивлений и гальванометра. В этой цепи R₁= 100 Ом, R₂=50 Ом, R₃=20 Ом, Э.Д.С. элемента ε₁=2 В. Гальванометр регистрирует ток I₃=50 мА, идущий в направлении, указанном стрелкой. Определить Э.Д.С. второго элемента. Сопро­тивлением гальванометра и внутрен­ним сопротивлением элементов пре­небречь.

Указание. Для расчета разветвленных цепей применяются законы Кирхгофа.

Первый закон Кирхгофа. Алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т.е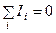

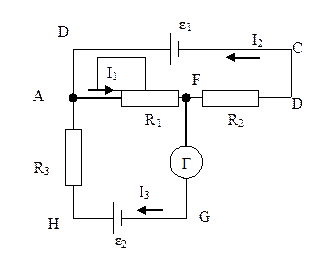
Второй закон Кирхгофа. В любом замкнутом контуре алгебраическая сумма напряжений на отдельных участках цепи равна алгебраической сумме Э.Д.С., встречающихся в контуре.

На основании этих законов можно составить уравнения, необходимые для определения искомых величин (сил токов, сопротивлений и Э.Д.С.). Применяя законы Кирхгофа, следует соблюдать сле­дующие правила:

1. Перед составлением уравнений произвольно выбрать: а) направления токов (если они не заданы по условию задачи) и указать их стрелками на чертеже; б) направление обхода контуров.

2. При составлении уравнений по первому закону Кирхгофа считать токи, подходящие к узлу, положительными; токи, отходящие от узла, отрицательными. Число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи.

3. При составлении уравнений по второму закону Кирхгофа надо считать, что: а) падение напряжения на участке цепи (т. е. произведение Ir) входит в уравнение со знаком плюс, если направление тока в данном участке совпадает с выбранным направлением обхода контура; в противном случае произведение Ir входит в уравнение со знаком минус; б) Э.Д.С. входит в уравнение со знаком плюс, если она повышает потенциал в направлении обхода контура, т. е. если при обходе приходится идти от минуса к плюсу внутри источника тока; в противном случае Э.Д.С. входит в уравнение со знаком минус.

Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, должно быть меньше числа замкнутых контуров, имеющихся в цепи. Для составления уравнений первый контур можно выбирать произвольно. Все последующие контуры следует выбирать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Если при решении уравнений, составленных указанным выше способом, получены отрицательные значения силы тока или сопротивления, то это означает, что ток через данное сопротивление в действительности течет в направлении, противоположном произвольно выбранному.

Решение. Выберем направления токов, как они показаны на рисунке, и условимся обходить контуры по часовой стрелке.

По первому закону Кирхгофа для узла F имеем: 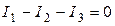(1)

По второму закону Кирхгофа имеем для контура ABCDFA:

,

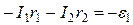или после умножения обеих частей равенства на -1

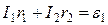(2)

Соответственно для контура AFGHA

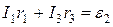(3)

После подстановки числовых значений в формулы (1), (2) и (3) получим:

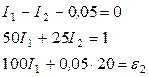
Эту систему с тремя неизвестными можно решить обычными при­емами алгебры, но так как по условию задачи требуется определить только одно неизвестное ε₂ из трех, то воспользуемся методом оп­ределителей.

Составим и вычислим определитель ∆ системы:

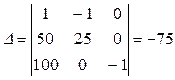
Составим и вычислим определитель ∆ε₂:

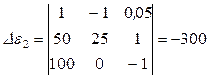
Разделив определитель ∆ε₂ на определитель ∆, найдем числовое значение ε₂ :

ε₂=-300/-75=4 В.

Ответ:ε₂=4 В.

Задача 16. Плоский квадратный контур со стороной 10 см, по которому течет ток силой 100 А, свободно установился в однородном магнитном поле индукции 1Тл. Определить работу, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол 90⁰. При повороте контура сила тока в нем поддерживается неизменной.

Решение. Как известно, на контур с током в магнитном поле действует момент силы : 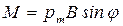(1)где 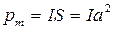-магнитный момент контура; 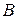-магнитная индукция; 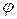-угол между векторам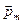и и .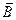

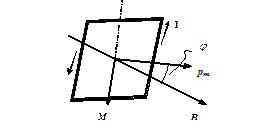
По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю М=0, а значит, 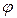=0, т.е. векторы 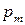и 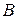сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота 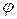), то для подсчета работы формулу работы в дифференциальной форме 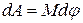. Учитывая формулу (1), получаем 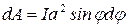. Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:

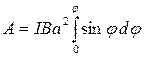
Работа при повороте на угол 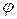=90⁰:

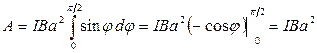(3)

Подставим в полученную формулу численные значения, получим: А=1Дж. Задачу можно решить и другим способом. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур:

,

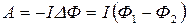где Ф₁ -магнитный поток, пронизывающий контур до перемещения;

Ф₂- то же, после перемещения.

Если 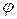=90⁰, то Ф₁=BS, Ф₁=0.

Следовательно, 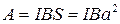, что совпадает с формулой (3).

Ответ:А=1Дж.

Задача 17. Электрон, пройдя ускоряющую разность потенциалов 400 В, попал в однородное магнитное поле напряженностью 1 кА/м. Определить радиус кривизны траектории и частоту обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

Решение. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца.

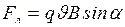
Сила Лоренца перпендикулярна вектору скорости, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона 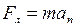, где 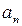- нормальное ускорение, или 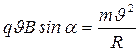(1)

где q- заряд, в нашем случае элементарный заряд; 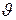-скорость электрона, В- магнитная индукция, m- масса электрона, R-радиус кривизны траектории, α - угол между векторами 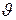и B (в данном случае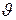 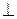В и 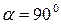, sin α=1).

Из формулы (1) найдем

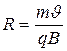(2)

Произведение 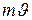, входящие в равенство (2), выразим через кинетическую энергию

.

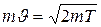Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов, можно определить 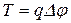. Подставив выражение T в формулу (3), получим

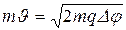(3)

Магнитная индукция может быть выражена через напряженность магнитного поля в вакууме:

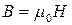(4)

где μ₀ -магнитная постоянная.

Подставив выражения (3) и (4) в формулу (2), получим

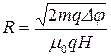
Произведя вычисления, получим: R= 5,37∙10^-2м.

Для определения частоты обращения воспользуемся формулой, связывающей частоту со скоростью и радиусом:

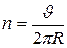(5)

Подставив в формулу (5) выражение (2), получаем

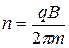или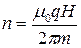

Произведя вычисления, получаем: n=3,52∙10⁷ с^-1 .

Ответ: R= 5,37∙10^-2м, n=3,52∙10⁷ с^-1 .

Задача 18. В однородном магнитном поле индукции 0,1 Тл равномерно с частотой 10 с^-1 вращается рамка, содержащая 1000 витков, плотно прилегающих друг к другу. Площадь рамки равна 150 см². определить мгновенное значение ЭДС индукции, соответствующие углу поворота рамки, равному 30⁰

Решение. Мгновенное значение ЭДС индукции определяется основным уравнением электромагнитной индукции Фарадея-Максвелла:

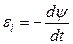(1)

где ψ – потокосцепление.

Потокосцепление связано с магнитным потоком и числом витков, плотно прилегающих друг к другу, соотношением

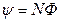(2)

.

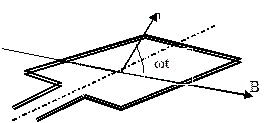Подставляя выражение (2) в формулу (1), получаем

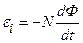
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, определяется соотношением 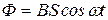, где B-магнитная индукция, S - площадь рамки, ω - круговая (или циклическая) частота.

Подставив в формулу (2) выражение Ф и продифференцировав полученное выражение по времени, найдем мгновенное значение ЭДС индукции:

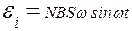(3)

Круговая частота ω связана с частотой вращения n соотношением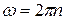

Подставляя выражение частоты в формулу (3) и заменив ωt на φ, получим

.

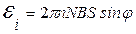Произведя вычисления, получим: 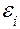=47,1 В.

Ответ: 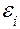=47,1 В.

Задача 19. На щель шириной 0,1 мм нормально падает параллельный пучок света от монохроматического источника (l= 0,6мкм). Определить ширину l центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии L = 1м.

Решение. Центральный максимум интенсивности света занимает область между ближайшими от него справа и слева минимумами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимуме интенсивности (см. рис.).

Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами j, определенными условием

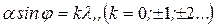(1)

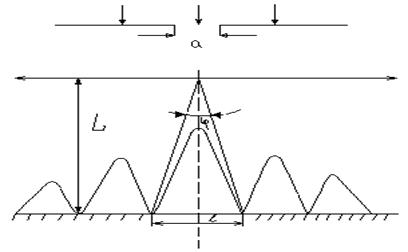
где k – порядок min , в нашем случае k =1. Расстояние между 2–мя минимумами на экране определим непосредственно по чертежу: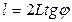

При малых углах 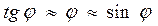, тогда 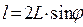(2).

Выразим sinj из формулы (1) и подставим его в равенство (2):

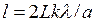(3)

Произведя вычисления по формуле (3), получим: l = 1,2 см.

Ответ: l = 1,2 см.

Задача 20. Пучок естественного света падает на полированную поверхность стекленной пластины, погруженной в жидкость. Отраженный от пластины пучок света составляет угол j = 97° с падающим пучком (см. рис.) Определить показатель преломления n₁ жидкости, если отраженный свет полностью поляризован.

Решение. Согласно закону Брюстера свет, отраженный от диэлектрика, полностью поляризован в том случае, если тангенс угла падения 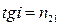, где n_2,1- относительный показатель преломления второй среды /стекла/ относительно первой /жидкости/, т.е. .

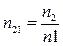По условию задачи, отраженный луч повернут на угол j относительно падающего луча.

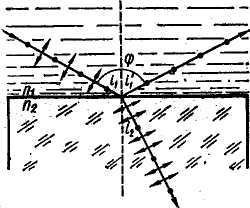Так как угол падения равен углу отражения, то 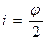и, следовательно, 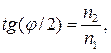откуда .

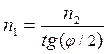Произведя вычисления, получим:

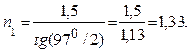
Ответ: п₁=1,33.

Задача 21. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела λ₀=0,58мкм. Определить энергетическую светимость (излучателность) R_e поверхности тела.

Решение. Энергетическая светимость R_e абсолютно черного тела в соответствии с законом Стефана - Больцмана пропорциональна четвертой степени термодинамической температуры и выражается формулой

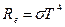(1)

где σ -постоянная Стефана - Больцмана; Т — термодинамическая температура.

Температуру Т можно выразить с помощью закона смещения Вина:

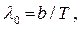(2)

где Ь — постоянная закона смещения Вина. Используя формулы (2) и (1), получаем

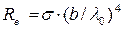(3)

Произведем вычисления:

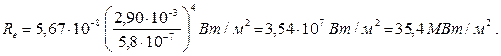
Ответ: R_e=35,4 МВт/м².

Задача 22.Определить красную границу l₀ фотоэффекта для металла, если при облучении его поверхности фиолетовым светом длиной волны l максимальная скорость υ_max фотоэлектронов равна 0,65 Мм/c.

Решение. При облучении светом с l₀, соответствующей красной границе фотоэффекта кинетическая энергия фотоэлектронов равна 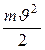. Уравнение Эйнштейна для фотоэффекта

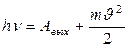(1)

В случае красной границы 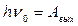и ,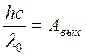

отсюда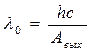

Работа выхода: 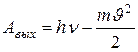(2).

Частота падающего света: 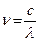(3).

Тогда с учётом (2), (3) : 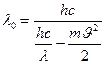(4).

Для определения красной границы фотоэффекта подставим значения в формулу (4) и вычислим : l₀ = 0,65мкм.

Ответ: l₀ =0, 65мкм.

Задача 23. Вычислить дефект массы ядра изотопа неона .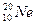

Решение. Дефект массы ядра равен

Dm = Zm_p + (A – Z)m_n – M_Я

Из символической записи элемента неона следует, что А = 20, Z = 10.

Тогда

Dm = 10m_p + (20 – 10)m_n – M_Я = 10 (m_p + m_n ) – М_Я .

По условию задачи:

m_p = 1,6724 × 10^-27кг, m_n = 1,6748 × 10^-27 кг, M_Я = 33,1888×10²⁷ кг.

Произведём вычисления:

Dm =10×(1,6724×10^-27 +1,6748×10^-27) - 33,1888×10^-27) кг =2,832×10^-28 кг.

Ответ: Dm=2,832×10^-28 кг.

Задача 24. Определить период полураспада радона, если за 1 сутки из 1 млн. атомов распадается 175 000 атомов.

Решение. Период полураспада радона

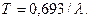
Постоянную радиоактивного распада l найдём из соотношения DN = N₀(1–e^-lt), откуда

.

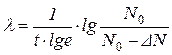Подставив это выражение в первую формулу, получим:

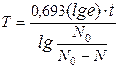; Т»3,3×10⁵с.

Ответ: Т»3,3×10⁵с.

Задача 25.В результате захвата a-частицы ядром изотопа азота 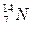образуются неизвестный элемент и протон. Написать реакцию и определить неизвестный элемент.

Решение. Запишем ядерную реакцию:

.

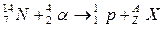Так как суммы массовых чисел и зарядов в правой и левой частях выражения должны быть равными, то

14 + 4 = 1 + А , 7 + 2 = 1 + Z,

откуда А = 17, а Z = 8.

Следовательно, полученный элемент символически можно записать в виде 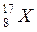. Изтаблицы Менделеева найдём, что это изотоп кислорода .

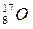Ответ: 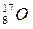.