Описание экспериментальной установки. Экспериментальная установка (рис
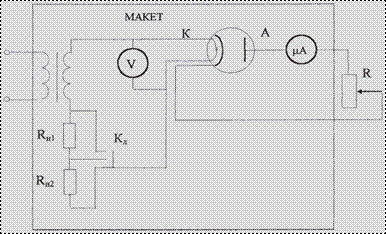 Рис. 2 Рис. 2 |
Экспериментальная установка (рис. 2) включает в себя экспериментальный макет и, подключаемый к нему, магазин сопротивлений R. Анодная цепь лампы, установленной в макете, состоит из микроамперметра и магазина сопротивлений, с помощью которого регулируют задерживающую разность потенциалов U. В цепи накала электронной лампы имеются резисторы Rн1, Rн2 и переключатель Кл, позволяющие дискретно менять мощность накала, и, соответственно, температуру катода электронной лампы. Напряжение от сети подается в цепь накала через понижающий трансформатор.
Порядок выполнения работы
1. Зарисовать таблицу
2. Подключить магазин сопротивлений к макету. Установить внешнее сопротивление R магазином сопротивлений 10 кОМ.
3. Включить макет в сеть 220 В и установить необходимый ток накала Iн электронной лампы с помощью переключателя Кл. Дать возможность лампе прогреться (при выходе на установившийся тепловой режим через окошечко в макете наблюдается светящийся термокатод, ток в анодной цепи лампы перестаёт расти).
4. Меняя внешнее сопротивление R в необходимых пределах (следить, чтобы стрелка микроамперметра не зашкаливала!), снять зависимость Ia от R (для 8-10 значений внешнего сопротивления). Данные рекомендуется занести в таблицу.
Таблица
| № | Iн, А | R, Ом | Ia × 10-6, А | U= Ia(R+Rm), В | lnIa |
| … |
5. При определении U учесть сопротивление микроамперметра Rm (Rm указано на приборе). Rm =2,5 кОм.
5. Повторить эксперимент для двух других значений токов накала. Данные занести в таблицы аналогичные приведенной.
Обработка результатов измерений
1. Для трех различных токов накала в одной системе координат построить графики зависимости lnIa=f (U). Убедиться в линейности графиков, т.е. в справедливости максвелловского распределения термоэлектронов по скоростям. При построении графиков рекомендуется использовать метод наименьших квадратов.
2. Учитывая, что угловые коэффициенты линеаризованных зависимостей в данной работе равны 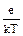 , а также используя табличные значения постоянных е и k, вычислить три различные температуры катода Т, соответствующие трём различным токам накала электронной лампы.
, а также используя табличные значения постоянных е и k, вычислить три различные температуры катода Т, соответствующие трём различным токам накала электронной лампы.
3. Используя формулы метода наименьших квадратов для расчета погрешностей коэффициентов линейной зависимости, оценить погрешности в определении температуры катода.
4. Определить среднеквадратичную, среднюю и наиболее вероятную скорости электронов для одного из найденных в работе значений температуры.
Контрольные вопросы
1. Как определить наиболее вероятную, среднюю и среднеквадратичную скорости молекул идеального газа из распределения Максвелла по скоростям?
2. Каковы формулы для среднеквадратичной и наиболее вероятной скоростей идеального газа, позволяющие найти эти скорости по известной температуре газа?
3. Каков вид распределения Максвелла по абсолютным значениям скорости и по проекциям скорости на ось х?
4. Какой вид имеет рабочая формула в данной работе ? Запишите ее.
5. В каких переменных строится график в данной работе?
6. Что служит причиной возникновения тока в анодной цепи?
7. Каким образом можно изменять задерживающую разность потенциалов при заданном напряжении накала?
8. Изменяется ли величина задерживающей разности потенциалов при изменении напряжения накала? Почему?
9. Каким образом изменяют температуру катода в данной работе?
Лабораторная работа № 10
Определение коэффициента теплопроводности металла
Цель работы: определение коэффициента теплопроводности металла и распределения температуры вдоль металлическогостержня, нагреваемого с одного конца.
Введение
Перенос тепла (энергии в форме теплоты Q) в твердых телах и газах описывается законом Фурье:
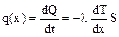 , (1)
, (1)
где q(x) – поток тепла, l - коэффициент теплопроводности, 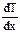 - градиент температуры, характеризующий ее убывание при удалении от источника тепла. Знак «минус» означает, что перенос энергии через площадку S происходит в сторону меньших температур.
- градиент температуры, характеризующий ее убывание при удалении от источника тепла. Знак «минус» означает, что перенос энергии через площадку S происходит в сторону меньших температур.
Коэффициент теплопроводности металлов меняется в широких пределах: от минимального (l ≈ 10 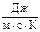 ) до максимального значения (у серебра l = 423
) до максимального значения (у серебра l = 423 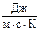 ), что значительно превышает коэффициент теплопроводности газов lгаза~ (10-2 ÷ 10-1)
), что значительно превышает коэффициент теплопроводности газов lгаза~ (10-2 ÷ 10-1) 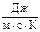 .
.
Процесс теплопроводности в твердых телах осуществляется путем взаимодействия колеблющихся ионов, образующих тело. Наиболее интенсивное колебание частиц, существующее в области повышенной температуры, передается соседним частицам, постепенно распространяясь на все тело.
Кроме того, теплопроводность в металлах значительно увеличивается благодаря наличию свободных электронов, которые могут перемещаться внутри металла, непосредственно перенося свою кинетическую энергию из области повышенной температуры в область более низкой. Важная роль свободных электронов в процессе теплопроводности подтверждается тем фактом, что теплопроводность металлов приблизительно пропорциональна их электропроводности.
Представим себе бесконечно длинный металлический стержень, один конец которого находится в печи (рис. 1).
Электроны и ионы, находящиеся в слое металла с координатой x вблизи печи, получают от неё дополнительную кинетическую энергию и передают её электронам и ионам соседнего слоя с координатой x+Dx. Стержень, получая тепло от печи, будет нагреваться. Одновременно с его поверхности часть тепла уносится воздушным потоком (конвекция). С течением времени устанавливается стационарное состояние, при котором распределение температуры вдоль стержня не меняется и имеет вид, показанный на рис.1.
Найдем уравнение теплопроводности, описывающее распределение температуры вдоль стержня.
Согласно (1) количество тепла, ежесекундно проходящее через сечение стержня S в точках x и (x +Dx), равно соответственно:
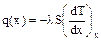 ,
, 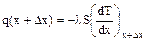 (2)
(2)
| радиатор Эл.печь S стержень T T = f (х) T0 0 х х+Dх х Рис. 1 Распределение температуры вдоль стержня. |
Количество тепла, отдаваемое с поверхности отрезком стержня между этими координатами, прямо пропорционально разности температур:
dq = αP(T – T0)dx, (3)
где a - коэффициент теплоотдачи металла, Р - периметр поперечного сечения стержня, Т, Т0 - температуры элемента стержня и воздуха соответственно.
В условиях стационарного режима количество тепла, поступающего в стержень, равно количеству тепла, отдаваемого им в окружающую среду, т.е. dq = q(x) – q(x + dx) или в соответствии с (2) и (3):
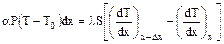 (4)
(4)
Учитывая, что:
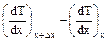 =
= 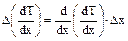 ≈
≈ 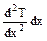 ,
,
при (Δx→dx) получим из выражения (4) дифференциальное уравнение второго порядка:
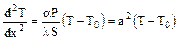 , (5)
, (5)
здесь:
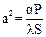 (6)
(6)
Уравнение типа (5) имеет стандартное решение вида:
T−T0 = Aeax + Be-ax, (7)
где А и В - произвольные постоянные.
По мере удаления от печи (х®¥) температура стержня убывает, приближаясь к комнатной (Т®Т0). Тогда уравнение (7) выполняется, если А = 0.
В начальной точке отсчета x = 0, Т = Т1. Тогда из (7)
В = Т1 - Т0. С учетом полученных значений А и В уравнение (7) примет вид:
T−T0 = (T1−T0)e-ax (8)
После логарифмирования получим формулу распределения температуры вдоль стержня в виде:
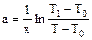 (9)
(9)
Рассчитаем тепло, теряемое бесконечно длинным отрезком стержня ежесекундно. Используя (3) и (8), запишем:
dq = αP(T – T0)dx = αP(T1−T0)e-axdx,
и после интегрирования получим:
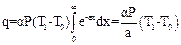
Согласно (6) αΡ = a2λS, тогда q = aλS(T1–T0), откуда:
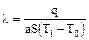
Подставив a из (9), получаем формулу для расчета коэффициента теплопроводности металла:
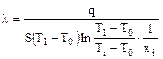 (10)
(10)
В формулу (10) входит разность абсолютных температур (по шкале Кельвина). Однако она равна разности температур по шкале Цельсия, т.е. Т1-Т0 = t1 – t0.
Количество тепла, ежесекундно отдаваемое электропечью, вычисляется по формуле:
q = hN, (11)
здесь N - мощность печи, h - её к.п.д. (коэффициент полезного действия) при теплоотдаче.
