Первый закон термодинамики
МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Тольяттинский Государственный Университет
Кафедра Водоснабжение и водоотведение
Л.Н. Козина
Теплотехника
(информационный курс)
Часть 1
Техническая термодинамика
Учебно-методическое пособие
Тольятти – 2010
Содержание
Стр.
1. Основные термодинамические понятия и определения 3
2. Параметры состояния 5
3. Законы идеальных газов 9
4. Смеси идеальных газов 11
5. Теплоёмкость газов 13
6. Первый закон термодинамики 18
7. Основные термодинамические процессы идеальных газов 20
Литература 27
Основные термодинамические понятия
И определения
Техническая термодинамика – часть общей Термодинамики, в которой рассматриваются закономерности превращения тепла в работу в различных тепловых машинах.
Термодинамическая система – совокупность макроскопических тел, обменивающихся энергией как друг с другом, так и с окружающей внешней средой.
Изолированная (замкнутая) система – система, которая не имеет никаких взаимодействий с окружающей средой.
Адиабатная (теплоизолированная) система – система, которая не обменивается теплом с окружающей средой.
Однородная система – система, которая во всех своих частях имеет одинаковые физические свойства и состав.
Гомогенная (однофазная) система – система, внутри которой нет поверхностей разрыва (однородна по составу и физическому строению).
Гетерогенная (многофазная) система – система, состоящая из нескольких макроскопических частей (фаз) с различными физическими свойствами, отделённых друг от друга видимыми поверхностями раздела.
Параметры состояния тела (системы) – некоторые физические величины, которые характеризуют данное физическое состояния тела.
Интенсивные параметры состояния - физические величины, не зависящие от массы системы (давление, температура и др.).
Экстенсивные (аддитивные) параметры состояния - величины, численное значение которых пропорционально массе системы (объём, энергия, энтропия и др.).
Основные термодинамические параметры состояния: удельный объём, абсолютная температура, абсолютное давление.
Примечание. Основные термодинамические параметры состояния не являются независимыми друг от друга величинами и связаны между собой уравнением состояния.
Равновесное состояние тела – состояние, когда во всех точках объёма тела давление, температура, удельный объём и все другие физические величины одинаковы.
Равновесный термодинамический процесс – совокупность изменений состояний термодинамической системы при переходе из одного равновесного состояния в другое.
Примечание. Только равновесные состояния могут быть описаны количественно с помощью уравнений состояния и только равновесные процессы можно изображать графически в системах координат P – vи T – s .
Изотермический процесс– равновесный процесс, в течение которого температура остаётся постоянной.
Изобарный процесс – равновесный процесс, протекающий при постоянном давлении.
Изохорный процесс– равновесный процесс, протекающий при постоянном объёме.
Адиабатный процесс– равновесный процесс, в котором термодинамическая система не обменивается теплом с окружающей средой.
Цикл (замкнутый или круговой процесс) – процесс, при котором система, проходя через ряд последовательных состояний, возвращается к начальному состоянию.
Внутренняя энергия газа– полный запас энергии (сумма отдельных видов энергий: кинетической энергии поступательного и вращательного движения молекул, колебательного движения атомов в молекулах, энергии электронов; внутриядерной энергии; энергии взаимодействия между ядром молекулы и электронами; потенциальной энергии, или энергии положения молекул).
Примечание. Внутренняя энергия не зависит от характера процесса и является функцией состояния, т.е. параметром (экстенсивным).
Теплота (количество теплоты) – энергия, переданная в процессе при непосредственном контакте тел, имеющих различную температуру, путём обмена кинетической энергии между молекулами соприкасающихся тел (микрофизическая форма передачи энергии).
Работа – энергия, переданная в процессе, связанном с перемещением тела в силовом поле, либо с изменением его объёма под действием внешних сил (макрофизическая форма передачи энергии).
Примечание. Тепло и работа являются функциями процесса.
Вопросы для самоконтроля
1. Какие основные вопросы рассматриваются в технической термодинамике?
2. Что называется равновесным состоянием?
3. Что такое термодинамические процессы и как они протекают?
4. Что называется термодинамической системой?
5. Дать определение гомогенной и гетерогенной системам.
6. Что называется функцией состояния?
7. Дать определение круговому процессу (циклу).
8. Какие существуют формы передачи энергии от одних тел к другим?
Параметры состояния
Величины, характеризующие состояние рабочего вещества называются параметрами состояния.
Параметры, которые можно измерить, называются основными. К основным параметрам рабочих веществ (пары или газы) относятся давление, плотность, удельный объем и температура.
Давление
Давление – это есть средний результат ударов молекул газа о стенки сосуда, в котором он находится. Давление измеряется силой, приходящейся на единицу площади поверхности. За единицу силы в системе СИ принят ньютон (Н):
1Н = 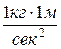 ;
;
за единицу давления – паскаль (Па), равный ньютону на квадратный метр:
1Па = 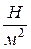 .
.
Эта единица давления очень мала, и пользоваться ей не всегда удобно. Для измерения больших давлений применяют единицы: килопаскаль (кПа) и мегапаскаль (МПа). При этом: 1 кПа = 10 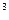 Па; 1 МПа = 10
Па; 1 МПа = 10 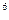 Па.
Па.
Исторически сложилось так, что в технике до сих пор широко используются ещё и внесистемные единицы давления.
Так, большие давления измеряют в технических атмосферах (ат) или в барах (бар):
1 ат = 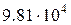 Па ;
Па ;
1 бар = 10 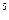 Па.
Па.
Малые давления измеряют в миллиметрах водяного столба (мм в.ст.) или в миллиметрах ртутного столба (мм рт.ст.). Обычно мм рт.ст используют для измерения атмосферного давления. Величина атмосферного давления, равная 760 мм рт.ст., называется физическая атмосфера (атм).
В термодинамике за параметр состояния рабочего вещества принимают абсолютное давление.
В технике давление выше атмосферного измеряют приборами, которые называются манометрами, а ниже атмосферного – вакууметрами. Все эти приборы показывают разницу между давлением в сосуде и атмосферным давлением. Поэтому для определения абсолютного давления рабочего вещества необходимо еще знать атмосферное давление, которое измеряется барометром. Таким образом,абсолютное давление обычно подсчитывается по показаниям двух приборов. Если абсолютное давление 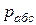 больше атмосферного, то оно рассчитывается по показаниям барометра и манометра, т.е.
больше атмосферного, то оно рассчитывается по показаниям барометра и манометра, т.е.
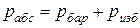 (2.1)
(2.1)
где 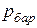 - атмосферное давление, определяемое барометром;
- атмосферное давление, определяемое барометром;
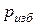 - давление по манометру (манометрическое, избыточное над атмосферным).
- давление по манометру (манометрическое, избыточное над атмосферным).
Если абсолютное давление меньше атмосферного, то оно подсчитывается по показаниям барометра и вакууметра, т.е.
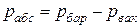 , (2.2)
, (2.2)
где 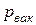 - давление вакуума, недостающее до атмосферного.
- давление вакуума, недостающее до атмосферного.
При удалении от поверхности земли атмосферное давление понижается. В пределах тропосферы (до высоты 11000 м) закон падения давления описывается формулой:
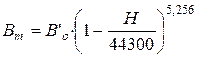 , (2.3)
, (2.3)
где 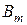 - барометрическое давление (мм рт.ст.) в тропосфере при температуре
- барометрическое давление (мм рт.ст.) в тропосфере при температуре
ртути 0 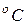 ;
;
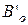 - барометрическое давление (мм рт.ст.) на уровне моря при
- барометрическое давление (мм рт.ст.) на уровне моря при
температуре ртути 0 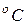 ;
;
Н- высота над уровнем моря, м.
При измерении давлений высотой столба жидкости необходимо учитывать изменение плотности жидкости в приборе в зависимости от температуры. При отклонении температуры жидкости в приборе от 0 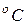 показание прибора приводят к температуре 0
показание прибора приводят к температуре 0 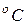 по формуле (для ртутного барометра):
по формуле (для ртутного барометра):
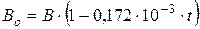 , (2.4)
, (2.4)
где 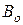 -атмосферное давление при температуре ртути0
-атмосферное давление при температуре ртути0 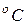 , мм рт.ст.;
, мм рт.ст.;
В- высота ртутного столба в барометре при температуре ртути 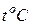 , мм рт. ст.
, мм рт. ст.
Можно также для ртути воспользоваться таблицей поправок:
Отклонение температуры ртутного столба от 0 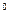 С С | 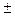 5 5 | 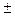 10 10 | 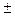 15 15 | 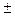 20 20 | 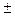 25 25 | 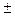 30 30 |
| Поправка х в мм на 1000 мм рт. ст. | 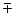 0,87 0,87 | 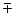 1,72 1,72 | 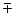 2,59 2,59 | 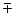 3,45 3,45 | 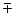 4,31 4,31 | 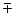 5,17 5,17 |
и измеренное ртутным барометром атмосферное давление В при температуре t привести к температуре ртути 0 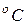 по формуле:
по формуле:
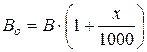 . (2.5)
. (2.5)
Таким образом, формулы (2.1) и (2.2) можно представить следующим образом:
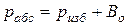 , (2.6)
, (2.6)
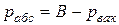 . (2.7)
. (2.7)
Плотность
В системе СИ плотность рабочего вещества определяется по формуле
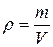 , (2.8)
, (2.8)
где m – масса рабочего вещества, кг;
V –объем, занимаемый рабочим веществом, 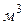 .
.
За единицу плотности принимается килограмм на кубический метр – 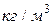 .
.
Удельный объем
Величина, обратная плотности, называется удельным объемом:
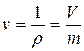 . (2.9)
. (2.9)
Таким образом, имеет место равенство:
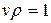 v. (2.10)
v. (2.10)
За единицу объема принимается кубический метр на килограмм 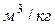 .
.
Температура
Температура характеризует степень нагретости газа и представляет собой меру средней кинетической энергии поступательного движения его молекул. При измерении температуры используют термометрическую и термодинамическую температурные шкалы, для которых соответственно установлены две единицы измерения: градус Цельсия ( 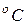 ) и градус Кельвина (
) и градус Кельвина ( 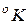 ). Для построения термометрической шкалы Цельсия выбраны две постоянные температуры (реперные точки) – таяния льда и кипения воды при нормальном атмосферном давлении. Первая принята за начало отсчета: 0
). Для построения термометрической шкалы Цельсия выбраны две постоянные температуры (реперные точки) – таяния льда и кипения воды при нормальном атмосферном давлении. Первая принята за начало отсчета: 0 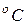 , вторая – за 100
, вторая – за 100 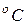 ; за градус принята 1/100 часть этого температурного интервала.Температура по шкале Цельсия обозначается t
; за градус принята 1/100 часть этого температурного интервала.Температура по шкале Цельсия обозначается t 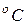 . Эта шкала используется для практического измерения температуры.
. Эта шкала используется для практического измерения температуры.
Термодинамическая шкала построена на основании второго закона термодинамики и называется также абсолютной. Эта шкала была предложена Кельвином и ею пользуются при измерении температуры ( Т ) от абсолютного нуля температур ( 0 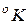 ). За реперную точку для этой шкалы принята тройная точка воды, т. е. температура, при которой могут одновременно существовать лед, вода и пар. Эта температура равна 273,16
). За реперную точку для этой шкалы принята тройная точка воды, т. е. температура, при которой могут одновременно существовать лед, вода и пар. Эта температура равна 273,16 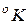 .
.
Градус Кельвина равен 1/273,16 части интервала от абсолютного нуля температуры до температуры тройной точки воды.
Температура точки таяния льда по шкале Цельсия на 0,01 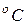 меньше температуры тройной точки. Поэтому по шкале Кельвина точка плавления льда имеет температуру 273,15 К.
меньше температуры тройной точки. Поэтому по шкале Кельвина точка плавления льда имеет температуру 273,15 К.
За параметр состояния рабочего вещества в термодинамике принимают термодинамическую (абсолютную) температуру
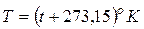 . (2.11)
. (2.11)
Нормальные условия
В термодинамике различают нормальные физические условия и нормальные технические условия.
Нормальные физические условия – это условия, при которых рабочее вещество находится под давлением 760 мм рт. ст. ( 1,0133 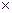 10
10 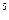 Па ) при температуре 0
Па ) при температуре 0 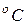 .
.
Нормальные технические условия – это условия, при которых рабочее вещество находится под давлением 1 кгс/см 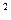 (0,980665
(0,980665 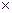 10
10 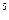 Па;735,6 мм рт. ст.) и t = 15
Па;735,6 мм рт. ст.) и t = 15 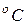 .
.
Объем газа, приведенный к нормальным условиям, принято обозначать:
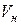 ,
, 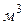 .
.
Вопросы для самоконтроля
1. Какие величины называются термодинамическими параметрами?
2. Какие термодинамические параметры относятся к основным?
3. Напишите размерность основных параметров.
4. Определите удельный объем и плотность газа.
5. В чем состоит различие между абсолютным и манометрическим (избыточным) давлением?
6. Какие температурные шкалы приняты в России?
7. Что называется абсолютной температурой?
8. Определение обратимого и необратимого процессов.
9. Каковы признаки обратимых процессов?
3. Законы идеальных газов
Газы, подчиняющиеся законам Бойля-Мариотта, Гей-Люссака, Авогадро и Дальтона, называются идеальными. Эти законы и соотношения, построенные на их основе, можно применять также к реальным газам при сравнительно невысоких давлениях и сравнительно высоких температурах.
С молекулярно-кинетической точки зрения идеальный газ – это газ, в котором отсутствуют силы взаимодействия между молекулами и пренебрегают объемом самих молекул.
Закон Бойля-Мариотта
При постоянной массе и одной и той же температуре плотность идеального газа изменяется прямо пропорционально, а удельный объем – обратно пропорционально давлению газа:
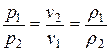 (3.1)
(3.1)
или
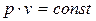 . (3.2)
. (3.2)
Закон Гей-Люссака
При постоянных давлении и массе удельный объем идеального газа изменяется прямо пропорционально, а его плотность - обратно пропорционально абсолютной температуре газа:
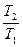 =
= 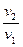 =
= 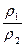 . (3.3)
. (3.3)
При объединении законов Бойля-Мариотта и Гей-Люссака получают уравнение Клапейрона для 1 кг газа
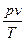 = const = R
= const = R
или
pv = RT , (3.4)
где R – газовая постоянная.
Размерность R , в соответствии с последним уравнением,
[ R ] = 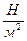
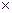
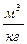
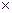
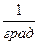 =
= 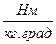 =
= 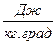
показывает, что эта величина является работой 1 кг газа при постоянном давлении и измененииего температуры на 1 К. Для идеального газа величина R зависит только от природы рабочего вещества.
Таким образом, уравнение Клапейрона связывает три основных термодинамических параметра: p, v,T и обычно используется для определения неизвестного параметра по двум заданным. Поэтому оно называется уравнением состояния идеального газа или его характеристическим уравнением.
Для G кг газа уравнение состояния:
pV = GRT . (3.5)
Закон Авогадро
При одинаковых температурах и давлениях в равных объёмах различных идеальных газов содержится одинаковое количество молекул.
Масса газа в килограммах, численно равная молекулярной массе, называется: килограмм-молекула или киломоль (кмоль). Из закона Авогадро следует, что произведение 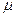 v (т.е. объём одного киломоля, где
v (т.е. объём одного киломоля, где 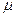 кг/кмоль – молекулярная масса однородного газа, а для смеси кажущаяся молекулярная или средняя молекулярная масса) есть величина одинаковая для всех газов и газовых смесей при одинаковых p и T . При нормальных физических условиях
кг/кмоль – молекулярная масса однородного газа, а для смеси кажущаяся молекулярная или средняя молекулярная масса) есть величина одинаковая для всех газов и газовых смесей при одинаковых p и T . При нормальных физических условиях
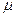 v = 22, 4 м
v = 22, 4 м 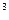 / кмоль. (3.6)
/ кмоль. (3.6)
Уравнение состояния для 1 кмоль газа называется уравнением Клапейрона - Менделеева и имеет вид
pV 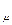 =
= 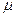 RT, (3.7)
RT, (3.7)
где
V 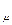 =
= 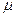 v,
v,
при этом
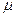 R = R
R = R 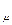 = 8,314 кДж /(кмоль
= 8,314 кДж /(кмоль 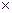 град.
град.
Величина R 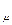 является универсальной газовой постоянной, одинаковой для киломоля любого однородного газа или газовой смеси. Универсальная газовая постоянная для 1 кг газа ( R ) определяется из соотношения
является универсальной газовой постоянной, одинаковой для киломоля любого однородного газа или газовой смеси. Универсальная газовая постоянная для 1 кг газа ( R ) определяется из соотношения
R = 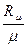 . (3.8)
. (3.8)
Вопросы для самоконтроля
1. Что называется уравнением состояния?
2. Для чего вводится в техническую термодинамику понятие об идеальном газе?
3. Законы Бойля – Мариотта и Гей-Люссака. Их определения и уравнения.
4. Что называется молекулярной массой газа?
5. Характеристическое уравнение состояния для идеального газа.
6. На каких законах основан вывод уравнения состояния Клапейрона?
7. Уравнение Клапейрона для любого количества газа.
8. Размерность всех величин, входящих в уравнение Клапейрона.
9. Размерность газовой постоянной и ее физический смысл.
10. Что называется киломолем газа?
11. Закон Авогадро, определение и выводы из этого закона.
12. На каких законах основан вывод уравнения Д. И. Менделеева?
13. Дать определение универсальной газовой постоянной и ее размерность.
Смеси идеальных газов
В качестве рабочих тел в технике могут использоваться смеси, состоящие из нескольких газов. Если смесь состоит из идеальных газов, то для неё справедливы все соотношения, полученные для однородного идеального газа. Так уравнение состояния для 1 кг смеси идеальных газов имеет вид:
pv = R 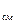 T . (4.1)
T . (4.1)
Для G кг смеси –
pV = G R 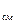 T , (4.2)
T , (4.2)
где R 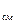 - газовая постоянная смеси, Дж / (кг
- газовая постоянная смеси, Дж / (кг 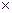 град) .
град) .
Для 1 кмоль смеси –
pV 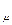 = R
= R 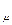 T . (4.3)
T . (4.3)
Здесь V 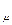 = v
= v 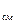
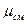 - объём 1 кмоль смеси;
- объём 1 кмоль смеси;
v 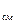 - удельный объём смеси, м
- удельный объём смеси, м 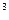 / кг;
/ кг;
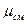 - кажущаяся или средняя молекулярная масса смеси, кг / кмоль;
- кажущаяся или средняя молекулярная масса смеси, кг / кмоль;
R 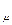 = 8314 Дж / (кмоль
= 8314 Дж / (кмоль 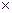 град) – универсальная газовая постоянная для смеси.
град) – универсальная газовая постоянная для смеси.
Для определения величин R 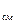 и
и 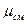 необходимо знать состав смеси, который может быть задан массовыми или объёмными долями.
необходимо знать состав смеси, который может быть задан массовыми или объёмными долями.
Массовая доля i-той составляющей газовой смеси:
g 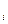 =
= 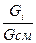 , (4.4)
, (4.4)
где G 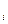 - масса данного газа в смеси, кг;
- масса данного газа в смеси, кг;
G 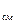 - масса смеси, кг.
- масса смеси, кг.
Сумма массовых долей:
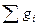 = 1. (4.5)
= 1. (4.5)
Каждый из газов, составляющих смесь, занимая объем, равный объему смеси, находится под своим парциальным давлением ( p 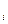 ) и имеет температуру смеси. Давление смеси равно сумме парциальных давлений. Это положение известно под названием
) и имеет температуру смеси. Давление смеси равно сумме парциальных давлений. Это положение известно под названием
закона Дальтона:
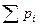 = p
= p 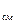 . (4.6)
. (4.6)
Объемная доля i-той составляющей газовой смеси:
r 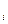 =
= 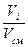 , (4.7)
, (4.7)
где V 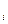 - объём данного газа, взятый при давлении смеси, так называемый приведенный
- объём данного газа, взятый при давлении смеси, так называемый приведенный
(парциальный)объём, м 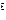 ;
;
V 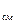 - объём смеси, м
- объём смеси, м 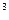 .
.
Сумма объёмных долей:
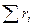 = 1. (4.8)
= 1. (4.8)
Сумма приведённых объёмов V 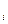 равна объёму всей смеси V
равна объёму всей смеси V 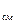 .
.
Если смесь задана массовыми долями, то R 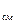 и
и 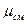 определяются из следующих соотношений:
определяются из следующих соотношений:
R 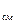 =
= 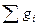 R
R 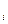 (4.9)
(4.9)
или
R 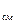 = 8314
= 8314 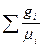 ; (4.10)
; (4.10)
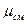 =
= 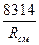 , (4.11)
, (4.11)
или
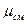 =
= 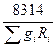 =
= 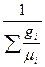 . (4.12)
. (4.12)
Если смесь задана объёмными долями, то справедливы зависимости:
R 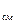 =
= 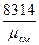 (4.13)
(4.13)
или
R 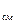 =
= 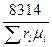 ; (4.14)
; (4.14)
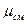 =
= 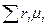 , (4.15)
, (4.15)
откуда
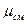 = 8314
= 8314 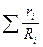 . (4.16)
. (4.16)
Парциальные давления отдельных газов, входящих в смесь, определяются из следующих соотношений:
1) если смесь задана массовыми долями, то
p 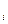 = g
= g 
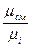 p
p 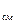 = g
= g 
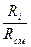 p
p 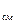 ; (4.17)
; (4.17)
2) если смесь задана объёмными долями, то
p 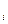 = r
= r 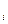 p
p 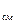 . (4.18)
. (4.18)
Соотношения между массовыми и объёмными долями составляющих газов и всей смеси в целом:
g 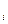 =
= 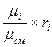 =
= 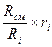 ; (4.19)
; (4.19)
r 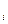 =
= 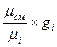 =
= 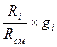 . (4.20)
. (4.20)
Вопросы для самоконтроля
1. Что такое газовая смесь?
2. Дать формулировку закона Дальтона.
3. Что называется парциальным давлением?
4. Что называется массовой, объёмной и мольной долями?
5. Что называется парциальным, или приведенным, объёмом?
6. Почему молекулярная масса смеси называется средней молекулярной массой?
7. Как производится пересчёт массового состава в объёмный и объёмного в массовый?
8. Как определяется газовая постоянная по массовым и объёмным долям?
9. Как определяется парциальное давление газа в смеси по массовым и объёмным долям?
10. Как определяется средняя молекулярная масса смеси газов?
Теплоёмкость газов
Теплоёмкостью называют количество тепла, необходимое для нагревания тела на один градус. Эта величина зависит от количества вещества в теле и является экстенсивным свойством.
В термодинамических расчётах используется теплоёмкость единицы количества вещества, которую называют удельной теплоёмкостью тела в данном процессе или просто теплоёмкостью. Эта величина является интенсивным параметром, т.е. удельная теплоёмкость не зависит от количества вещества в системе.
В зависимости от того, к какой количественной единице отнесена теплоёмкость, в термодинамике различаются:
1) массовая теплоёмкость c 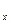 , кДж/(кг град) – для 1 кг;
, кДж/(кг град) – для 1 кг;
2) объёмная теплоёмкость c 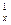 , кДж/(м
, кДж/(м 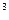 град) – для 1 м
град) – для 1 м 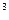 , взятого при
, взятого при
нормальных физических условиях, т.е. при давлении 101 325 Па
( 760 мм рт. ст. ) и температуре 0 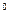 С;
С;
3) мольная теплоёмкость 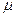 c
c 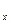 , кДж/(кмоль град) – для 1 кмоль газа.
, кДж/(кмоль град) – для 1 кмоль газа.
Между указанными выше теплоёмкостями существует следующая взаимосвязь:
c 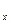 = c
= c 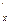 v
v 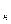 =
= 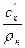 =
= 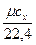 , (5.1)
, (5.1)
где v 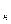 и
и 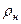 – соответственно, удельный объём и плотность при нормальных
– соответственно, удельный объём и плотность при нормальных
физических условиях;
x – индекс, который указывает на тот параметр ( p, v и др.), при
постоянном значении которого происходит рассматриваемый процесс.
Сообщение телу теплоты в каком-либо процессе вызывает изменение его состояния и, в общем случае, сопровождается изменением температуры. Предел отношения теплоты 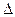 q
q 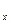 , полученной единицей количества вещества при бесконечно малом изменении его состояния, к изменению температуры
, полученной единицей количества вещества при бесконечно малом изменении его состояния, к изменению температуры 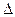 t называют истинной теплоёмкостью тела в данном процессе:
t называют истинной теплоёмкостью тела в данном процессе:
c 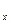 =
= 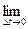
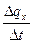 =
= 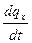 . (5.2)
. (5.2)
Фактически, это теплоёмкость при данных значениях параметров состояния v и T , или p и T (т.е. в данном состоянии тела).
В общем случае теплоёмкость не является постоянной величиной.
Для идеального газа теплоёмкость зависит от его физических свойств (прежде всего от его атомности), температуры, характера процесса, а для реальных газов – и от давления.
Иногда в теплотехнических расчётах, не требующих большой точности, особенно в области сравнительно невысоких температур и при небольших интервалах, пренебрегают зависимостью теплоёмкости от температуры и считают её величиной постоянной.
В связи с зависимостью теплоёмкости от температуры вводится понятие средней теплоёмкости в интервале температур, которой называют отношение
c 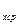 =
= 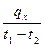 , (5.3)
, (5.3)
где q 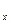 – теплота,
– теплота,
t 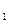 и t
и t 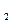 - температуры начала и конца процесса.
- температуры начала и конца процесса.
Таким образом, количество тепла в процессе нагревания или охлаждения рабочего тела можно определить, если известны средняя теплоёмкость процесса, температуры начала и конца процесса и количество вещества.
В общем случае зависимость теплоёмкости от температуры имеет нелинейный характер, поэтому каждому значению температуры соответствует своё значение истинной теплоёмкости. Эта зависимость описывается полиномом
c 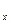 = a + bt + dt
= a + bt + dt 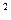 + ... , (5.4)
+ ... , (5.4)
где a, b, d, … -постоянные для каждого газа величины, определяемые на основании
экспериментальных или теоретических данных.
При нелинейной зависимости теплоёмкости от температуры вычисление средних теплоёмкостей в интервале температур t 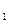 и t
и t 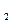 представляет значительные трудности. Поэтому, для наиболее распространённых газов определены экспериментально и приведены в справочных таблицах средние теплоёмкости в интервале от нуля до какой-либо температуры t. При этом температура t принимает различные, всё увеличивающиеся на определённый интервал (например, на 100
представляет значительные трудности. Поэтому, для наиболее распространённых газов определены экспериментально и приведены в справочных таблицах средние теплоёмкости в интервале от нуля до какой-либо температуры t. При этом температура t принимает различные, всё увеличивающиеся на определённый интервал (например, на 100 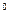 C) значения температур. Обычно в таблицах задаются значения мольных средних теплоёмкостей для процессов, протекающих при p = const и различных температурах (см. Приложение 4).
C) значения температур. Обычно в таблицах задаются значения мольных средних теплоёмкостей для процессов, протекающих при p = const и различных температурах (см. Приложение 4).
К примеру, средняя мольная теплоемкость в произвольном диапазоне температур от t 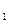 и t
и t 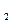 в изобарном процессе при использовании табличных данных определяется по формуле
в изобарном процессе при использовании табличных данных определяется по формуле
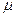 c
c 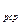 =
= 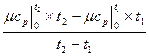 , кДж/(кмоль град), (5.5)
, кДж/(кмоль град), (5.5)
где 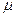 c
c 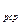 - средняя мольная теплоемкость в диапазоне температур от t
- средняя мольная теплоемкость в диапазоне температур от t 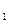 до t
до t 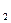 (
( 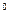 C),
C),
кДж/(кмоль град);
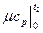 - средняя мольная теплоемкость в интервале температур от 0 до t
- средняя мольная теплоемкость в интервале температур от 0 до t 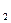
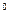 C ,
C ,
кДж/(кмоль град);
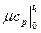 - средняя мольная теплоемкость в интервале температур от 0 до t
- средняя мольная теплоемкость в интервале температур от 0 до t 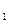
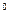 C,
C,
кДж/(кмоль град);
t 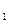 , t
, t 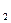 - температуры начала и конца процесса,
- температуры начала и конца процесса, 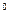 C .
C .
Тогда, средняя массовая теплоемкость в изобарном процессе определяется по формуле:
