Ток смещения. Уравнения Максвелла
Теория электромагнитного поля, начала которой заложил Фарадей, математически была завершена Максвеллом. При этом одной из важнейших новых идей, выдвинутых Максвеллом, была мысль о симметрии электрического и магнитных полей. А именно, поскольку меняющееся во времени магнитное поле создает электрическое поле, следует ожидать, что меняющееся во времени электрическое поле создает магнитное поле. Так как магнитное поле есть основной обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения.
 |
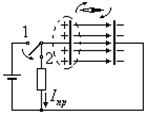Предположение Максвелла о существовании тока смещения, сопровождающегося магнитным полем, было подтверждено экспериментально А.А. Эйхенвальдом (Россия начало 20-го века). Один из многочисленных опытов Эйхенвальда заключался в том, что магнитная стрелка, подвешенная вблизи плоского заряженного конденсатора, отклонялась при разряде конденсатора от своего первоначального направления. Убывающее электрическое поле между обкладками конденсатора представляет собой ток смещения, сопровождающийся, как и ток проводимости, магнитным полем, действующим на магнитную стрелку.
Применим теорему Гаусса к замкнутой поверхности охватывающей одну из пластин конденсатора
,
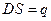где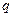 
— заряд на пластине; 
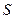— площадь пластины. Возьмем производную по времени от левой и правой части последнего равенства
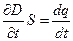или 
,
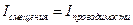т. е. цепь оказывается замкнутой. Благодаря току смещения. Плотность тока смещения будет равна
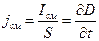, или в векторной форме
.
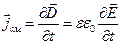Если в каком либо проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле. Поэтому внутри проводника имеется и ток проводимости, и ток смещения. Сумму же тока проводимости и тока смещения называют полным током. Его плотность
.
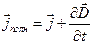Тогда теорему о циркуляции вектора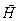 
, которая была установлена для постоянных токов , можно обобщить для произвольного случая и записать
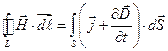, (1)
или в дифференциальной форме
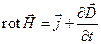. (1)
Уравнения Максвелла представляют собой обобщение уже рассмотренных нами законов. Рассмотрим эти уравнения в интегральной и дифференциальной форме.
Уравнение (1) выражает закон, по которому магнитное поле порождается токами проводимости и смещения.
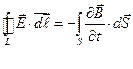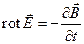; (2)
. (2)
Уравнение (2) выражает закон электромагнитной индукции и указывает на изменяющееся магнитное поле как на один из возможных способов получения электрического поля.
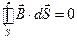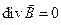(3)
(3)
Уравнение (3) есть теорема Гаусса для магнитного поля и выражает замкнутость силовых линий.
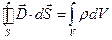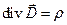(4)
(4)
Уравнение (4) есть теорема Гаусса для электрического поля.
Эти четыре уравнения называются полевыми и применимы для описания всех макроскопических электромагнитных явлений.
Чтобы учесть электромагнитные свойства материальной среды вводится дополнительно еще три уравнения — материальные уравнения.
, 
, 
.
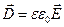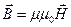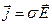Система уравнений Максвелла позволяет рассчитать любой электромагнитный процесс. Принципиальное значение имеют два первые уравнения, позволяющие ввести понятие электромагнитной волны.