Цикл Карно, теорема Карно, обратный цикл Карно
Карно рассмотрел обратимый круг. пр. Этот пр. сост. из 4-х обрат. процессов: двух изотермич. и двух адиаб. Цикл Карно сыграл большую роль в развитии термод. и теплотехники, т.к. позволяет проводить анализ кпд тепл. двиг. На рис. прямой цикл Карно: /-/’ изотерм. расшир. при Т1 (Т1’ = Т1), адиабатного расш. 1’-2, изотер. сжатие 2-2’ при Т2 (Т2 = Т2’) и адиаб. сжатие 2’-1. Процесс проходит так:
Газ в цилиндре с подвижным поршнем, в процессе изотерм. расш. находится в тепл. контакте с равновес. раб. телом при Т1. Это тело наз. нагреватель. – большой резервуар с водой. В процессе H’ нагреватель передает газу теплоту Q1>0. Теплоемкость нагревателя д.б. бесконечно большой (иначе Т нагревателя стала бы уменьш. и нарушалась бы изотермичность порц.). В проц. 1’-2 газ полностью теплоизолируют и его расширение происходит адиабатно. Для этого на участке 1’-2 цикла его необх. разобщить с нагревателем и заключил в теплонепр. оболочку. На участке 2-2’ газ приводят в тепл. контакт с др. телом, имеющим Т2 (Т2< Т1) - холодильником. В пр. 2-2’газ изотермически сжимается и передает холодильнику теплоту – Q2. Затем, в сост 2’ газ снова теплоизолируется и адиабатно сжимается до первонач. сост. 1, где цикл. К. заверш.
Работа, кот. соверш. раб. тело в прямом цикле К. равна
A = Q = Q1-Q2
т.е. A< Q1, т.е. полезная работа меньше энергии, получ. в формк теплоты от нагр. на количество тепл., отданное хол. Этот результат справедлив для любого прямого круг. проц.:
А1 соверш. за прямой цикл всегда меньше к-ва теплоты, подводимого всеми нагревателями.
Величина η = А/Qподв. – отнош. работы А, соверш. раб. телом в прямом обр. цикле, к кол-ву тепл. Qподв сообщенному в этом проц. раб. телу нагрев, наз. термическим кпд цикла. Он характ. экономичность цикла тепл. двиг. Для прямого цикла A = Q1-Q2, а Qподв. = Q1 тогда кпд цикла
η = (Q1-Q2)/Q1
 Далее будет показано, что η зависит только от Т нагр. и Т хол.
Далее будет показано, что η зависит только от Т нагр. и Т хол.
η = (Т1-Т2)/Т1 = 1- Т2/Т1 (**)
Из последних ф-л видно, что (Q1-Q2)/Q1 = (Т1-Т2)/Т1 или

1 - Q2/Q1 = 1 - Т2/Т1 => Q1/Т1 Q1/Т1+ Q2/Т2 = 0
При выводе ф-лы (**) не делалось никаких предположений о свойствах раб. тела и устройства тепл. машины (ф-ла теорет.). След-но кпд всех обратимых машин, работающих в один. условиях (т.е. при одинак. Т1 и Т2) одинаков и определ только температурами нагревателя и холод. – Это теорема Карно.
В обр. цикле К. отводится к-во тепл. Q1 в процессе 1’-1 – изотерм. сжатие при Т1, а к-во теплоты Q2 подводится к газу в процессе 2’-2 изотермич. расшир. при Т2< Т1. След-но Q1<0; Q2>0 и работа, совершаемая газом за цикл отрицательна A = Q1-Q2<0. Этот вывод справедлив для любого обратного цикла. Если раб. тело сов. обр. цикл, то при этом идет передача теплоты от холл. тела к горячему за счет соверш. внешними силами соответств. работы. По такому принципу работают холодильники.
Величина Σ равная отнош. Qотв теплоты, отведенной в обр. цикле от охлажд. тела, к работе А’, затраченной в этом цикле, наз. холодильным коэффициентом.
Σ = Qотв/ А’
В частности для обр. цикла Карно Qотв = Q2 А’ = -А = Q1-Q2, а связь между Q1 и Q2 такая же, как в прямом цикле, т.е.
Σ = Q2/(Q1-Q2) = Т2/(Т1-Т2)
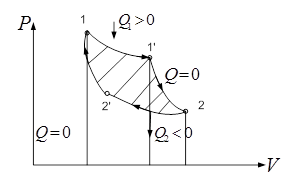 рис.19
рис.19
4.4 Энтропия
В середине ХІХ века было сделано существенное открытие, касающееся обратимых т. процессов. Оказалось, что наряду с внутренней энергией у тела имеется еще одна важная функция состояния – энтропия. Так же, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. В опытах проявляется значение разности энтропий (энтропия от греческого слова преобразовать, превратить).
Если тело или система при бесконечно малом переходе из одного состояния в другое при темпратуре Т получает малое количество теплоты δQ, то отношение δQ/Т является полным дифференциалом некоторой функции S. Эта функция и есть энтропия, определяющаяся, таким образом, двумя эквива
| |
dS = δQ/Т, а после интегрирования: ΔS = S2-S1 = ∫ δQ/Т
Открытие этого принципа связано с именами Карно и Клаузиуса, и является существенной частью 2-го з-на т.
Переход системы из одного состояния в другое может произойти бесчисленным количеством способов (разные кривые на графике с окончанием в одних
| |
Например, тело нагревают равномерно от 20 до 25˚С, при этом оно получает по 5 Дж теплоты на 1 К. Тогда прирост энтропии, примерно, равен S2-S1 ≈ 5/293,5+5/294,5+5/295,5+5/296,5+5/297,5 Дж/К. Наиболее просто выразить изменение энтропии при изотермическом процессе: S2-S1 = Q/Т
За нуль энтропии может быть принято значение энтропии любого состояния, (кипящей воды, плавящегося льда). Однако, в некоторых случаях за нуль
| |
S = ∫ νСрdT/T если нагрев происходил при р= const. Чтобы определение энтропии dS = δQ/Т было обоснованным, необходимо доказать, что в любом обратимом круговом процессе интеграл от δQ/Т тождественно равен 0.

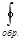 δQ/Т ≡0, т.е. S = const
δQ/Т ≡0, т.е. S = const
Если известно уравнение состояния вещества, то энтропия (с точностью до const) может быть вычислена весьма просто. По определению:
dS = δQ/Т , подставив сюда δQ из 1-го з-на т. получим:
dS = (m/M)(CvdT/T+RdV/V)
Взяв определенный интеграл, получим S2-S1 = (m/M)(Cv lnT2 /T1+ RlnV2/V1).
Это выражение для энтропии идеальных газов: она возрастает с повышением Т и при увеличении объема газа при подводе к телу теплоты δQ.
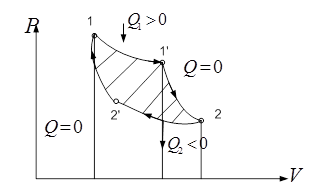 рис.20
рис.20
