Кинетические коэффициенты
1.3.1.В этом параграфе мы познакомимся с эмпирическими законами, описывающими поведение диффузионных потоков. Мы увидим, что основной экспериментальный факт состоит в том. что величина этих потоков определяется степенью пространственной неоднородности соответствующих интенсивных макроскопических величин: чем сильнее различаются значения этих величин в разных частях системы, тем больше величина диффузионных потоков. Микроскопическому объяснению этих законов будут посвящены остальные параграфы настоящей лекции.
1.3.2.Рассмотрим систему, находящуюся при определенной температуре и определенном давлении и состоящую из частиц двух сортов. Пусть полная плотность числа частиц п = п1 + п2 одна и та же во всей системе, а состав частиц не однороден в пространстве из-за того, что плотности числа частиц каждого сорта, п1 и п2, меняются от точки к точке. Основным эмпирическим законом, описывающим диффузионные потоки в такой системе, является закон Фика, который связывает поток частиц s-го сорта, dJs (s = 1, 2), протекающий через элементарную площадку dA, с быстротой изменения плотности их числа,  dns/dx, в направлении нормали
dns/dx, в направлении нормали 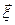 :
:
 .
.
Величину D, определяемую этим законом, называют коэффициентом диффузии частиц s-го сорта в данной смеси веществ.
В соответствии с законом величина потока частиц зависит, во-первых, от местоположения площадки dA. Потому что в разных участках пространства плотность числа частиц может по-разному меняться от точки к точке, и поэтому будет различна производная dns/dx,. И, во-вторых, поток через данную площадку зависит еще от ее ориентации в пространстве, определяемой направлением нормали 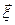 .
.
Пусть, например, плотность числа частиц меняется только в направлении оси х, оставаясь постоянной в плоскостях 11' и 22', показанных на Рис. 1‑2. Тогда производная dn/dx, будет максимальна для площадки с нормалью вдоль оси х. При любой другой ее ориентации расстояние dx, между плоскостями 11' и 22', отсчитываемое в направлении нормали 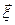 , будет больше, а изменение плотности на этом расстоянии — такое же. Поэтому отношение dn/dx, уменьшится, свидетельствуя об уменьшении потока через такую наклонную площадку. Это происходит, конечно, потому, что поток всегда имеет определенное направление, и если мы будем ориентировать площадку плоскостью вдоль этого направления, то через нее ничего не будет протекать.
, будет больше, а изменение плотности на этом расстоянии — такое же. Поэтому отношение dn/dx, уменьшится, свидетельствуя об уменьшении потока через такую наклонную площадку. Это происходит, конечно, потому, что поток всегда имеет определенное направление, и если мы будем ориентировать площадку плоскостью вдоль этого направления, то через нее ничего не будет протекать.
 Рис. 1‑2 Рис. 1‑2 |
При неоднородном составе частиц диффузия происходит в любых системах. В газах она идет довольно быстро, в жидкостях — медленнее, а в твердых телах — совсем медленно, но все же идет.
1.3.3.Если температура Т в остальном однородной системы меняется от одной точки к другой, через произвольную площадку dA возникает поток тепла
 .
.
Это соотношение, выражающее эмпирический закон Фурье, определяет величину κ, называемую коэффициентом теплопроводности. Производная dT/dx, имеет здесь тот же смысл, что и производная dn/dx в формуле : она определяется быстротой изменения температуры в направлении 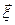 .
.
1.3.4.Между различными частями неподвижных газа или жидкости действуют силы только одного типа — силы нормального давления. Если же разные слои жидкости или газа движутся друг относительно друга, то, помимо этих обычных сил давления[1], между ними начинают действовать еще силы вязкого трения, стремящиеся затормозить их относительное движение. Такая ситуация возникает, например, при пролете через жидкость или газ какого-нибудь тела, которое вовлекает в свое движение прилегающие к нему слои вещества. При обтекании жидкостью или газом различных препятствий или при их движении по трубам, когда тормозятся слои, прилегающие к неподвижным предметам. И так далее.
 Рис. 1‑3 Рис. 1‑3 |
Разнообразие движений здесь огромно, и, чтобы разобраться в существе дела, ограничимся простейшим случаем ламинарного потока, текущего вдоль оси у со скоростью Vy, различной в разных точках оси х (Рис. 1‑3). В этом случае в любой плоскости АА' действуют две одинаковые по величине и противоположные по направлению силы трения, одна из которых приложена к правой части среды, а другая — к левой. Эти силы направлены, соответственно, по и против оси у и ускоряют движение более медленных слоев (на Рис. 1‑3 — правых), но тормозят движение более быстрых (на Рис. 1‑3 — левых). В результате вся среда приобретает с течением времени одинаковую скорость (если есть неподвижные стенки, то нулевую). Эмпирический закон Ньютона устанавливает, что величина этих сил
 ,
,
где h — коэффициент внутреннего трения или вязкость, A —площадь сечения АА'.
Этот закон можно представить в виде, аналогичном виду законов Фика и Фурье . Из-за действия вязкой силы у-компонента импульса левой от сечения АА' части среды убывает со скоростью  , а правой — с такой же скоростью возрастает. Мы можем сказать поэтому, что y-компонента импульса переносится через сечение АА' слева направо, и ее поток
, а правой — с такой же скоростью возрастает. Мы можем сказать поэтому, что y-компонента импульса переносится через сечение АА' слева направо, и ее поток

(если dVy/dx < 0, как на Рис. 1‑3, то  и наоборот).
и наоборот).
1.3.5.Коэффициенты диффузии, теплопроводности и вязкости, вводимые законами —, относятся к числу величин, называемых кинетическими коэффициентами. А пространственные производные, фигурирующие в этих соотношениях, называют градиентами — градиентом плотности числа частиц, градиентом температуры и градиентом у-компоненты скорости[2].
Универсальная справедливость законов — связана просто с тем, что в малом все линейно, и если различные диффузионные потоки исчезают в однородной системе, когда все градиенты равны нулю, то при малых градиентах они должны быть им пропорциональны. Такие соображения не позволяют, конечно, выяснить, как малы должны быть градиенты, чтобы линейность еще не нарушалась. Опыт показывает, однако, что реально создаваемые градиенты различных макроскопических параметров в этом смысле практически всегда достаточно малы.
