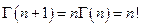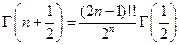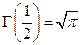Квазиклассическое приближение в статистической физике

Мы говорили, что состояние квантово-механической системы описывается каноническим распределением:

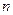, где - номер состояния

Потом учли, что энергетические уровни близко расположены друг к другу и ввели вместо дискретного спектра – непрерывный:

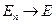
Ввели функцию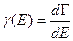

В нормировке функции перешли к интегралу:

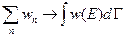
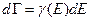- это число состояний в интервале энергий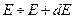

Здесь 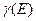- плотность состояний с энергией 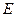на единичный интервал энергии.

Мы вместо 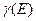часто пользуемся функцией :

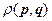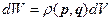, где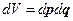

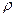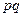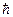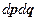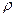Функция - размерная. Величина имеет размерность , тогда объёмчик имеет размерность . Значит, функция имеет размерность

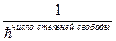
Поэтому удобно ввести величину:

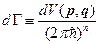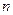, - число степеней свободы системы

Тогда:

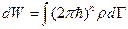(здесь уже безразмерные величины)

При 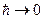имеем квазиклассическое приближение. В этом случае 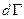характеризует величину числа состояний в интервале .

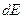Как же посчитать число состояний при переходе из фазового пространства в квазиклассическое представление?

В квантовой механике:

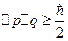
т.е. это точность, с которой определяется фазовая точка в фазовом пространстве.

Но фазовая точка определяет состояние, тогда это точность, с которой определяется состояние:

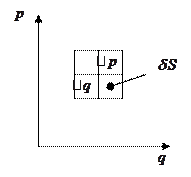
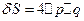
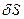- это площадка, описывающая состояние.

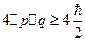-точнее этого мы состояние не определим.

Более точные измерения дают:

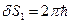
- такая площадка выделяется на фазовую точку (в случае, когда 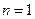- одна степень свободы).

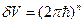
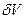- это объём, приходящийся на одно состояние в квазиклассическом приближении, при 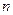степенях свободы.

Тогда: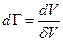

где 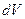- элементарный объём фазового пространства, а 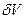- объём на одно состояние, следовательно 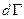- число состояний.

Тогда в квазиклассическом приближении каноническое распределение выглядит так:

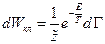
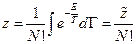
Множитель 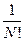возникает по следующим причинам:

В квантовом случае 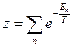- суммирование по числу состояний, и мы учитывали нетождественные перестановки. Но интегрирование по фазовому пространству не чувствительно к тождественным перестановкам – не выбрасываем их, поэтому возник множитель 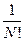- учитывающий тождественные перестановки. Это имеет место при переходе в квазиклассическое приближение.

Замечание:

Принцип тождественности оказывает влияние только на расчёт статистического интеграла 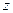, при расчёте средних он не влияет.

Каноническое распределение для квантовых систем имеет вид:

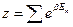- суммирование по квантовым состояниям

При переходе в квазиклассику, используя переход 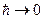, получаем для вероятности состояния 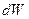(здесь индекс не проставлен):

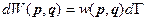
где 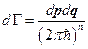и ,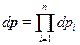

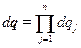
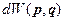- это вероятность того, что фазовая точка с координатами 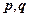попадает в элементарный объём 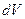в фазовом пространстве.

Мы писали: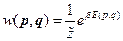

под 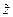понимаем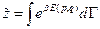

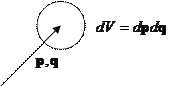Очевидно, что константу 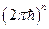можно выкинуть, если рассчитывать средние через вероятность, при переходах:

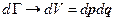
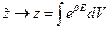
т.к. константа 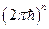не влияет на расчёт средних.

Часто рассматривают случай, когда квазиклассичность имеет место не по всем степеням свободы, а лишь по некоторым. Тогда суммируем по квантовым степеням свободы и интегрируем по квазиклассическим степеням свободы, т.е. имеем «гибрид»:

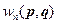
и в этом случае имеется и статистическая сумма и статистический интеграл.

§21*. Распределение Максвелла как следствие канонического распределения Гиббса

Далее будем излагать без константы 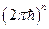, т.к. она нам в ближайших расчётах не понадобится.

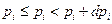
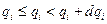
здесь 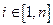, а 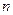- число степеней свободы.

В квазиклассике:

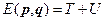
Рассмотрим систему из 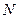материальных точек и в качестве 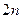степеней свободы выберем 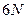переменных:

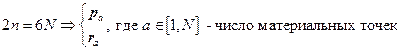
т.е. это обычное трехмерное пространство.

Тогда можем в явном виде записать кинетическую энергию и аргументы потенциальной энерги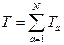и:

и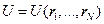

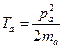
здесь время 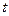отсутствует, потому что решается стационарная задача.

И функция плотности вероятности и вероятность зависят от всех выше указанных переменных:

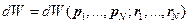(15)

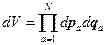
Каждый вектор 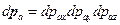- т.е. это элементарный объём соответствующего трёхмерного пространства.

Вероятность 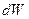говорит о событии:

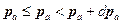
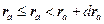
где .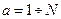

Если имеем вероятность некоторого совместного события:

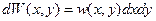
то вероятность одного из них:

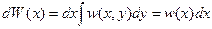
тогда:

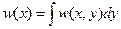(16)

Используем соотношение (16), чтобы, зная вероятность (15), найти плотность распределения импульсов (в данном случае импульса первой точки):

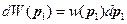
Аналогично (16) получаем:

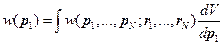здесь 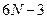интегралов

Для функции 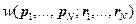имеем:

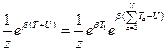
При интегрировании функция 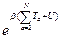даст константу, а 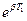выносится за интеграл тогда:

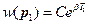
Из условия нормировки найдём константу :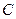

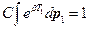
Далее индекс «1» ставить не будем, т.к. если все точки одинаковы, то нет смысла выделять точку (для всех точек распределение будет одинаковое).

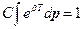и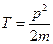

(Далее Т – температура)

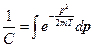
Тогд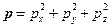а:

, а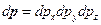

все переменные меняются в пределах от 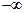до 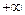, тогда получаем:

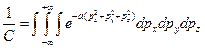
где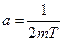

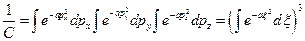
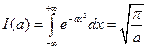
Тогда получаем:

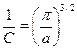
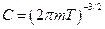
Само распределение имеет вид:

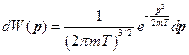
Мы получили распределение вероятностей импульсов или распределение Максвелла. Хотя его ещё называют распределением Больцмана.

Эта вероятность говорит о событии:

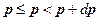
здесь три неравенства, т.к. имеется три проекции импульса.

§22. Использование распределения Максвелла для расчёта средних: , , ,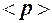

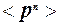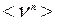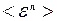
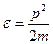- кинетическая энергия

Посмотрим .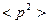

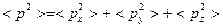
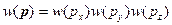
Если рассмотрим 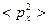, то получим:

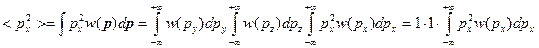
Запишем выражение для :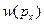

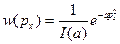
Подставим в наше выражение, тогда получим:

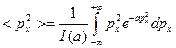
Тогда мы можем записать:

,

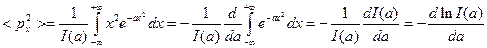
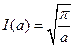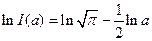
Тогда:

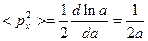
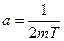
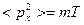
Аналогичные результаты имеем для 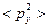и 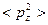, тогда:

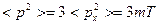
Легко найти :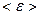

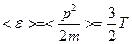
здесь 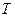- температура в энергетических единицах.

При расчёте 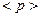в произвольной степени 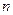, имеет место другая схема расчёта, а именно:

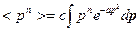, где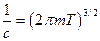

При нечётном 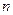надо учитывать симметричность 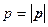, т.е. 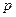- получается чётная функция. В этом сложность расчёта. Поэтому для расчёта переходят в сферические координаты:

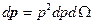
Тогда:

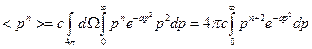
Сделаем замену переменных:

, ,

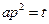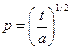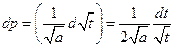
Тогда получим:

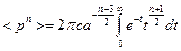
Используем гамма функцию :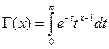

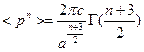
Из свойств гамма функции замечаем такие соотношения: