Вывод выражений для основных термодинамических величин больцмановского газа
Свободная энергия одной компоненты записывается в общем виде как сумма по всем состояниям системы:
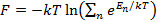 (2.1)
(2.1)
Используя то, что в каждом из возможных молекулярных состояний может оказаться не больше одной частицы, то от суммирования по состояниям системы можно перейти к суммированию по уровням энергии одной молекулы
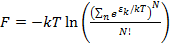 , (2.2)
, (2.2)
где 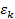 – энергия одной молекулы.
– энергия одной молекулы.
Т.к. N 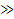 1 и по формуле Стирлинга
1 и по формуле Стирлинга 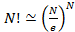 , то:
, то:
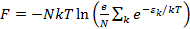 (2.2)
(2.2)
Далее записывая полную энергию в виде: 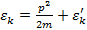 , где:
, где:
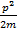 - кинетическая энергия поступательного движения;
- кинетическая энергия поступательного движения;
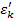 - энергия внутренних степеней свободы;
- энергия внутренних степеней свободы;
и переходя от суммирования к интегрированию по всем состояниям, получаем:
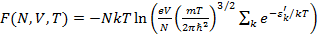 (2.3)
(2.3)
Введем  и перепишем (2.3) в виде:
и перепишем (2.3) в виде:
F 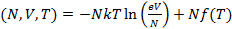 (2.4)
(2.4)
Формула (2.4) и есть выражение для свободной энергии.
Если взять частную производную 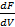 , то получим выражение для давления газа:
, то получим выражение для давления газа:
P = 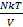 , или, если умножить на объем:
, или, если умножить на объем:
PV = 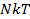 (2.5)
(2.5)
Теперь, зная F можно получить остальные термодинамические величины.
Запишем термодинамический потенциал Гиббса:
G 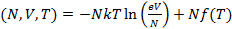 +PV (2.6)
+PV (2.6)
Подставим в (2.6) выражение (2.5). Получим:
G 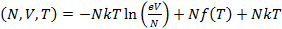 (2.7)
(2.7)
Введем новую функцию температуры:
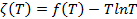 (2.8)
(2.8)
С учетом (2.8) и (2.7) получим выражение для термодинамического потенциала Гиббса:
G 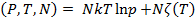 (2.9)
(2.9)
Известно, что термодинамический потенциал связан с химическим потенциалом соотношением:
G 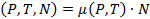 (2.10)
(2.10)
Т.е, для получения выражения для химического потенциала необходимо поделить формулу (2.9) на число частиц N:
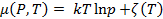 (2.11)
(2.11)
Найдем химический потенциал в переменных (T,V), для этого нужно взять частную производную:
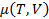 =
= 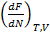 =
= 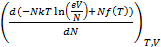
Распишем по свойству логарифмов:
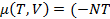 ln(eV)+NTln(N)+N
ln(eV)+NTln(N)+N 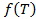 )’
)’
Конечное выражение для химического потенциала имеет вид:
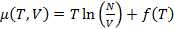 (2.12)
(2.12)
Энтропия находится как:
S(T,P,N)= 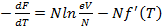 (2.13)
(2.13)
Используя (2.5) преобразуем выражение (2.13) в функцию P и T:
S(P,T)= 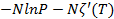 , (2.14)
, (2.14)
Внутренняя энергия равна:
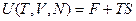 (2.15)
(2.15)
Дифференциал свободной энергии равен:
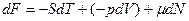 (2.16)
(2.16)
Подставим в (2.16) выражения:
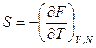
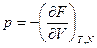
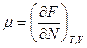
И затем подставим в (2.15) полученные равенства и уравнение свободной энергии:
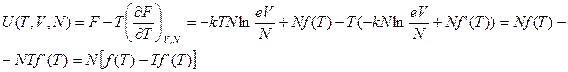
Упростим, получим:
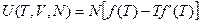 (2.17)
(2.17)
Аналогично:
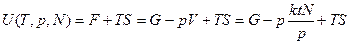 (2.18)
(2.18)
Подставим выражения:
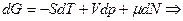
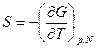
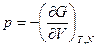
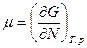
Получим:
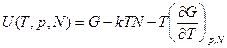 (2.19)
(2.19)
Найдем термодинамический потенциал Гиббса:
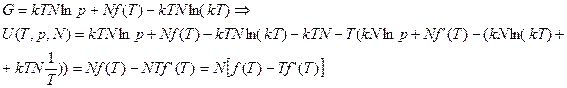
Подставим в (2.19), получим:
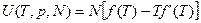 (2.20)
(2.20)
Так как формулы (2.17) и (2.20) одинаковы, то делаем вывод, что внутренняя энергия для больцмановского газа не зависит от объема и давления.
Теплоемкости также являются функциями, не зависящими от P и V:
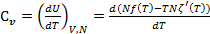 (2.21)
(2.21)
Вычислим производную, получим:
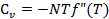 (2.22)
(2.22)
По формуле Маера, зная 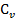 , найдем
, найдем 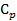 :
:
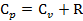 (2.23)
(2.23)
Где R-универсальная газовая постоянная, равная 8,31 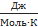 .
.
3.Вывод формул для вкладов колебаний атомов в свободную энергию, во внутреннию энергию, в энтропию и в теплоемкость 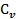 газов.
газов.
Необходимо рассмотреть отдельно двухатомную и многоатомную молекулы.
В двухатомной молекуле есть только одна колебательная степень свободы, так как колебания атомов происходят вдоль прямой, соединяющей их ядра.
Если колебания малы, т. е. 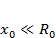 и Т
и Т  Тдисс, то колебательные уровни энергии двухатомной молекулы записываются так:
Тдисс, то колебательные уровни энергии двухатомной молекулы записываются так:
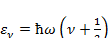 (3.1)
(3.1)
где  — частота колебаний, a v =0,1,2,... колебательное квантовое число.
— частота колебаний, a v =0,1,2,... колебательное квантовое число.
Колебательная статистическая сумма для одной молекулы запишется:
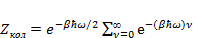 (3.2)
(3.2)
Где 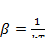 .
.
Ряд в (3.2) – геометрическая прогрессия 1+q+ 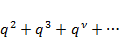 , где q=
, где q= 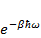 .
.
Как известно из математики, сумма бесконечно убывающей геометрической прогрессии описывается формулой:
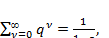 (3.3)
(3.3)
Используя (3.3) получим в (3.2):
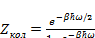 (3.4)
(3.4)
Свободная энергия молекулярного газа разобьется на сумму нескольких слагаемых.
F = Fпост+ Fэл+ Fкол+ Fвращ. (3.5)
Где свободная энергия колебания равна:
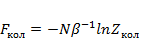 (3.6)
(3.6)
Подставим (3.4) в (3.6), получим:
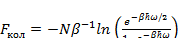 (3.7)
(3.7)
Для расчета внутренней энергии найдем сначала 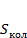 :
:
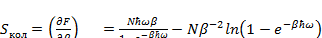 (3.8)
(3.8)
Вспомним формулу (2.15):
U(T,N)=F+TS, (3.9)
Подставим в (3.9) выражение (3.8) и (3.7):
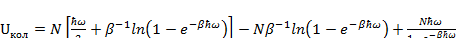 (3.10)
(3.10)
Упростим выражение (3.10), получим:
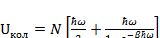 (3.11)
(3.11)
Из выражения (3.11) находится вклад колебаний в теплоемкость газа 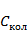 :
:
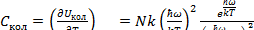 (3.12)
(3.12)
В сложных молекулах, состоящих из трех и более атомов, существует несколько различных типов колебаний ядер около равновесных положений. Если молекулы газа устойчивы, т.е. температура газа значительно меньше, чем температура диссоциации T дисс = Е дисс/k, то колебания малы и колебательные уровни энергии молекулы описываютя формулой:
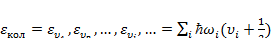 (3.13)
(3.13)
где vi независимо друг от друга принимают значения 0,1, 2,....
Из выражения (3.13) можно получить выражение для статистической суммы:
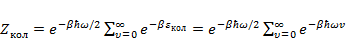 (3.14)
(3.14)
Это геометрическая прогрессия:
1+q+ 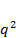 +…
+… 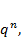 где q=
где q= 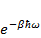
Как известно, сумма геометрической прогрессии вычисляется так:
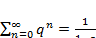 (3.15)
(3.15)
C учетом (3.15) получим в (3.14) следующее:
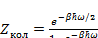 (3.16)
(3.16)
Выражение для свободной энергии колебаний молекул будет иметь вид:
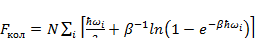 (3.17)
(3.17)
Где 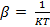 .
.
Каждая мода колебаний атомов вносит аддитивный вклад в свободную энергию газа. Найдем вклад в энтропию:
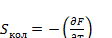 (3.18)
(3.18)
Вычислив частные производные получим:
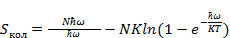 (3.19)
(3.19)
Выражение для внутренней энергии тогда будет иметь вид:
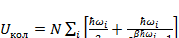 (3.20)
(3.20)
Выражение для теплоемкости будет иметь вид:
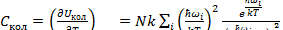 (3.21)
(3.21)
Приложение 1
Докажем, что условие 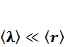 и условие
и условие 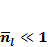 эквивалентны.
эквивалентны.
Для этого выведем из первого условия выражение, которое можно получить и из второго условия.
Запишем для начала:
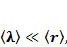 (1.1)
(1.1)
Вспомним:
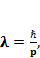 (1.2)
(1.2)
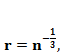 (1.3)
(1.3)
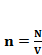 ,
,  (1.4)
(1.4)
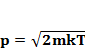 (1.5)
(1.5)
Подставим (1.2), (1.3), (1.4) и (1.5) в наше условие (1.1), получим:
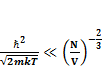 (1.6)
(1.6)
После некоторых преобразований мы получаем выражение:
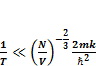 (1.7)
(1.7)
Из выражения (1.7) мы получаем:
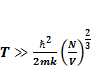 (1.8)
(1.8)
Сведем к выражению (1.8) и второе условие:
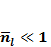 (1.9)
(1.9)
Вспомним:
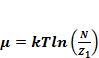 (1.10)
(1.10)
Используя формулу (1.10) и выражение для статистической суммы получим выражение:
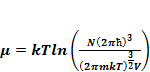 (1.11)
(1.11)
Используя условие того, что химический потенциал больцмановского газа всегда меньше нуля и 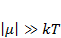 запишем:
запишем:
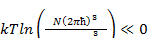 (1.12)
(1.12)
Сократим на kT и представим 0 как ln1. Получим:
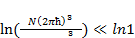 (1.13)
(1.13)
После преобразований получим выражение:
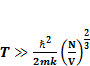 (1.14)
(1.14)
Это выражение соответствует (1.8), ч.т.д.
Приложение 2.
Согласно распределению Гиббса, вероятность 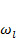 того, что в тепловом равновесии частица находится в стационарном состоянии , |l> имеет вид
того, что в тепловом равновесии частица находится в стационарном состоянии , |l> имеет вид
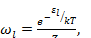 (2.1)
(2.1)
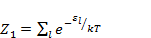 (2.2)
(2.2)
Где 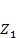 — одночастичная статистическая сумма.
— одночастичная статистическая сумма.
Из формулы (2.1) для средней энергии частицы равновесного больцмановского газа:
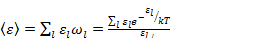
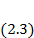
Средняя энергия всего газа запишется так:
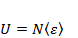
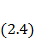
Так как число частиц газа N очень велико, то, согласно общим принципам теории вероятности получим распределение Больцмана:
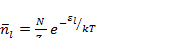 (2.5)
(2.5)
Расчетная часть.
Экспериментальное значение характеристической температуры для колебаний атомов в молекуле NO составляет 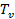 =2690 K.
=2690 K.
1) Вывести приближенные выражения для вклада колебаний атомов 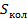 в энтропию газообразного NO в предельных случаях
в энтропию газообразного NO в предельных случаях 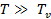 и
и 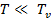 .
.
2) Вывести приближенные выражения для вклада колебаний атомов 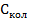 в молярную теплоемкость газообразного NO в предельных случаях
в молярную теплоемкость газообразного NO в предельных случаях 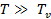 и
и 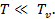
3) Оценить вклад колебаний молекул в молярную теплоемкость газа NO при комнатных температурах T~20 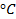 и сравнить его с вкладом поступательного движения молекулы.
и сравнить его с вкладом поступательного движения молекулы.
4) Построить и обсудить графики зависимости 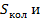
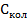 от температуры газа NO.
от температуры газа NO.
1. Воспользуемся формулой (3.16) для выражения 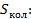
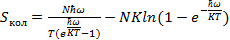 (4.1)
(4.1)
По определению характеристическая температура равна:
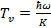 (4.2)
(4.2)
С учетом (4.2) получим в (4.1)
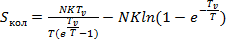 (4.3)
(4.3)
Рассмотрим предельный случай 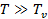 .[4]
.[4]
При высоких температурах можно произвести разложение по степеням 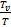 и ограничиться первыми членами разложения:
и ограничиться первыми членами разложения:
Разложим в ряд 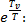
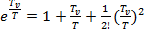 +
+ 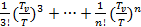 (4.4)
(4.4)
И в ряд 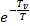 :
:
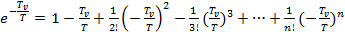 (4.5)
(4.5)
Возьмем первые два члена ряда:
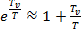 (4.6)
(4.6)
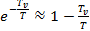 (4.7)
(4.7)
Подставим (4.6) и (4.7) в (4.4). Получим:
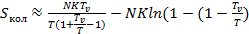 ) (4.8)
) (4.8)
После преобразований:
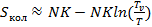 (4.9)
(4.9)
Рассмотрим второй предельный случай: 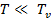 .[4]
.[4]
В данном случае 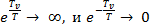 , поэтому в первом слагаемом
, поэтому в первом слагаемом 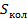 в формуле (4.3) пренебрежем единицей, а во втором слагаемом получится логарифм от единицы:
в формуле (4.3) пренебрежем единицей, а во втором слагаемом получится логарифм от единицы:
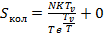 (4.10)
(4.10)
Запишем иначе:
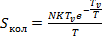 (4. 11)
(4. 11)
Так как 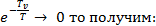
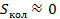 (4.12)
(4.12)
Т.е, в случае 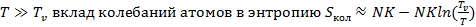 .
.
Где 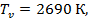 возьмем количество частиц, равное одному молю. Тогда N=6,02⋅
возьмем количество частиц, равное одному молю. Тогда N=6,02⋅ 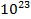 , постоянная k = 1,38⋅
, постоянная k = 1,38⋅ 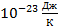 .
.
В случае 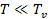 вклад колебаний атомов в энтропию
вклад колебаний атомов в энтропию 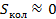 .
.
2. Вывести приближенные выражения для вклада колебаний атомов 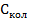 в молярную теплоемкость газообразного NO в предельных случаях
в молярную теплоемкость газообразного NO в предельных случаях 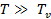 и
и 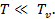
Вспомним формулу для вклада колебаний атомов 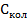 в молярную теплоемкость ( 3.11):
в молярную теплоемкость ( 3.11):
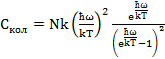 (5.1)
(5.1)
По определению характеристическая температура равна:
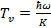 (5.2)
(5.2)
Запишем выражение (5.1) с учетом (5.2):
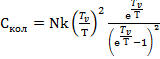 (5.3)
(5.3)
Рассмотрим предельный случай 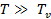 :
:
Можно, аналогично п.1 расчетной части, произвести разложение по степеням 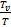 и ограничиться первыми членами разложения (5.4).
и ограничиться первыми членами разложения (5.4).
Разложение 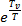 в ряд представлено в выражении (4.4).
в ряд представлено в выражении (4.4).
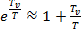 (5.4)
(5.4)
С учетом (5.4) перепишем (5.3):
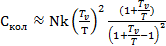 (5.5)
(5.5)
После преобразований получим:
 (5.6)
(5.6)
Так как 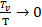 то:
то:
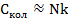 (5.7)
(5.7)
Во втором предельном случае, когда 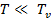 .
.
Запишем выражение (5.3):
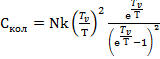 (5.8)
(5.8)
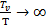 ,
, 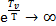 , значит единицей можно пренебречь:
, значит единицей можно пренебречь:
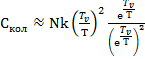 (5.9)
(5.9)
Произведем небольшие преобразования:
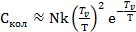 (5.10)
(5.10)
Экспонента 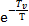 убывает быстрее, чем растет
убывает быстрее, чем растет 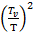 :
:
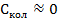 (5.11)
(5.11)
В предельном случае, когда 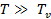 имеем
имеем 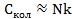 , в предельном случае, когда
, в предельном случае, когда 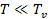 имеем
имеем 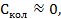 возьмем количество частиц, равное одному молю, тогда.N =6,02⋅
возьмем количество частиц, равное одному молю, тогда.N =6,02⋅ 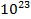 , постоянная k = 1,38⋅
, постоянная k = 1,38⋅ 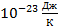 .
.
3. Оценить вклад колебаний молекул в молярную теплоемкость газа NO при комнатных температурах T~20 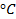 и сравнить его с вкладом поступательного движения молекулы.
и сравнить его с вкладом поступательного движения молекулы.
Воспользуемся формулой (5.3):
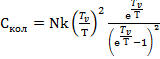 (6.1)
(6.1)
Подставим значения T=293K, 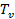 =
= 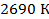 , также возьмем один моль частиц, тогда.N=Na⋅моль, где постоянная Na=6,02⋅
, также возьмем один моль частиц, тогда.N=Na⋅моль, где постоянная Na=6,02⋅ 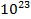
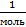 , постоянная k = 1,38⋅
, постоянная k = 1,38⋅ 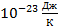 .
.
Получим:
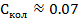
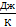 (6.2)
(6.2)
Необходимо вывести выражение для 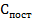 . Для этого найдем сначала
. Для этого найдем сначала 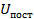 :
:
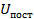 =
= 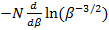 =
= 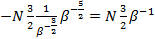 (6.3)
(6.3)
Где 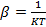 .
.
Подставив выражение для 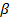 в (6.3) получим:
в (6.3) получим:
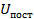 =
= 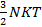 (6.4)
(6.4)
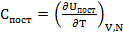 =
= 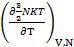 =
=  NK (6.5)
NK (6.5)
Подставим в (6.5) постоянную k = 1,38⋅ 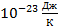 и возьмем количество частиц, равное одному молю, тогда N=6,02⋅
и возьмем количество частиц, равное одному молю, тогда N=6,02⋅ 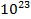 , постоянная k = 1,38⋅
, постоянная k = 1,38⋅ 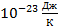 .
.
Получим:
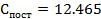
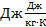 (6.6)
(6.6)
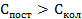
Графики
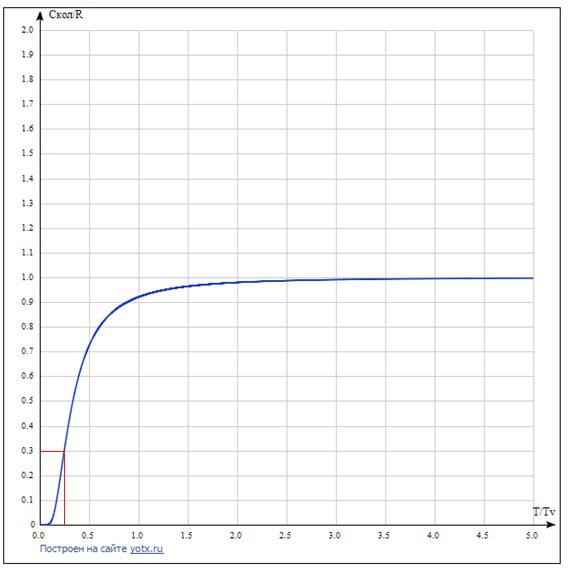
График зависимости безразмерной температуры от безразмерной теплоемкости.
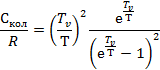
Искомая величина  при Т = 1275 К равна 2. 493 Дж/К (точка на графике при
при Т = 1275 К равна 2. 493 Дж/К (точка на графике при 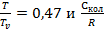 = 0.3)
= 0.3)
В
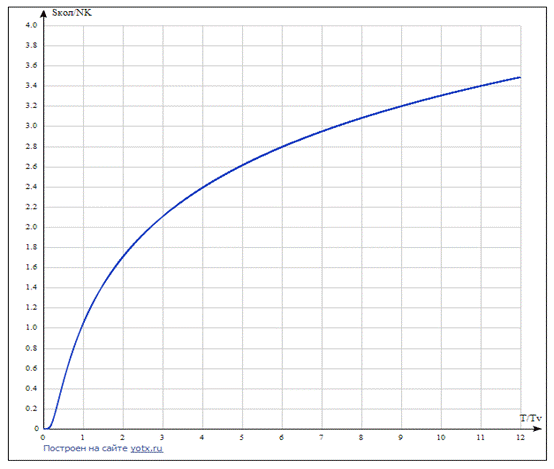
График зависимости безразмерной температуры от безразмерной энтропии.
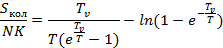
Вывод:
Мы рассмотрели, как ведет себя 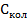 при
при 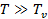 и при
и при 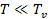 . При
. При 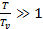
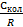 стремится к единице, при
стремится к единице, при 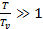
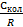 стремится к нулю.
стремится к нулю.
Теплоемкость газов зависит только от геометрии молекул газа, которая позволяет определить число степеней свободы вращательного и колебательного движений. По классической теории теплоемкостей газов получается, что теплоемкость газов не зависит от рода газа и не зависит от температуры.
Сравнение этой теории теплоемкостей с экспериментом показало, что эта теория хорошо согласуется с экспериментом только при высоких температурах, а при низких температурах наблюдается существенное расхождение теоретических и экспериментальных результатов. Для объяснения этих расхождений в классической физике было введено понятие о «замораживании» степеней свободы. Согласно этому представлению, молекулы газа при средних и низких температурах не совершают колебательного движения.
Мы рассмотрели, как ведет себя 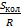 при
при 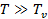 и при
и при 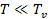 . При
. При 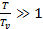
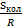 стремится к бесконечности, при
стремится к бесконечности, при 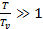
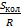 стремится к нулю.
стремится к нулю.
Это согласуется с теоремой Нерста: «При приближении к абсолютному нулю абсолютная энтропия системы стремится также к нулю независимо от того, какие значения принимают при этом все параметры, характеризующие состояние системы»
(Абсолютная энтропия – энтропия равновесной системы, при абсолютном нуле температур она равна нулю)
Также из теоремы Нерста следует, что теплоемкости всех тел при приближении к абсолютному нулю температур так же стремятся к нулю.
Список использованной литературы.
1. Компанеец А. С. Курс теоретической физики. Том 2 Статистические законы.М.: Просвещение, 1975, - 450 с.
2. Коткин Г. Л. Лекции по статистической физике. Новосибирск: редакционно-издательский отдел новосибирского университета, 2005, – 172 с.
3. Ландау Л.Д., Лившиц Е. М. Статистическая физика. Часть 1. – М.: Наука, 1974. – 586.
4. Левич В. Г. Курс теоретической физики. Том 1. М.: Наука, 1969. – 912 с.
5. Морозов В. Г., Фетисов Ю. К. Молекулярная физика. Курс физики, часть 1. М.: Мирэа, 2010, - 98 с.
6. Шиллинг Г. Статистическая физика в примерах. М: Мир, 1976, - 433 с.
