Правила Кирхгофа для разветвленных цепей

(Густов Роберт)Г. Кирхгоф (1824–1887) детально исследовал закон Ома и разработал общий метод расчета постоянных токов в электрических цепях. Этот метод основан на двух правилах, называемых законами Кирхгофа.

Первый закон Кирхгофа устанавливает связь между токами ветвей в узле электрической цепи.

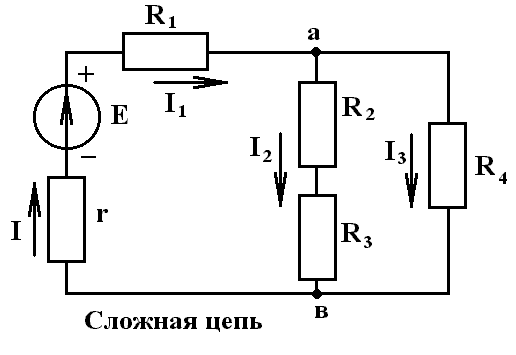
Ветвь электрической цепи или схемы – участок, элементы которого соединены последовательно. Место (точка) соединения ветвей называют узлом (а, в) электрической цепи или схемы. Любой путь вдоль ветвей электрической цепи, начинающийся и заканчивающийся в одной и той же точке называетсяконтуром.

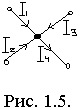Первое правило Кирхгофа относится к узлам, то есть точкам, в которых сходится не менее трех проводников. В любой точке цепи, в том числе в любом узле, имеющийся заряд должен оставаться постоянным, поэтому сумма притекающих к узлу токов должна быть равна сумме вытекающих. Условились считать подходящие к узлу токи положительными, а исходящие – отрицательными. Для узла выполняется закон сохранения заряда – сколько заряда переносится к узлу втекающими токами, столько же заряда выходит из узла, т.е. в узле заряды не накапливаются и не исчезают.

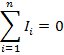
где n – номер ветви в узле.

Первый закон Кирхгофа: алгебраическая сумма токов ветвей в узле электрической цепи, в любой момент времени, равна нулю.

Поскольку токи, направленные к узлу, считаются положительными, а токи, направленные от узла, — отрицательными, первый закон Кирхгофа можно записать в виде:

I₁+I₂+I₃- I₄=0,или .

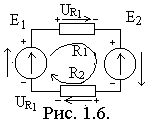Второй закон Кирхгофа. Он устанавливает связь между напряжениями на элементах контура (рис. 1.6). Для замкнутого контура, также выполняется закон сохранения энергии. Каждый узел или точка электрической цепи обладает собственным потенциалом и, перемещая заряд вдоль замкнутого контура, мы совершаем работу, которая при возврате заряда в исходную точку будет равна нулю. Это свойство потенциального электрического поля и описывает второй закон Кирхгофа в применении к электрической цепи:

В любом замкнутом контуре алгебраическая сумма падений напряжений на элементах равна нулю вне зависимости от направления обхода контура, т.е. ,

где k – номер элемента контура.

При расчете сложных цепей с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, а если - отрицательным - его истинное направление противоположно выбранному.

2. Выбрать направление обхода контура и строго его придерживаться; произведение IRположительно, если ток на данном участке совпадает с направлением обхода. ЭДС, действующие по выбранному направлению обхода, считаются положительными, против -отрицательными.

3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, чтобы не получались уравнения, которые являются простой комбинацией уже составленных уравнений.

Для схемы на рис. 1.6 второй закон Кирхгофа записывается следующим образом:

U_R1 + U_R2 – E₁+Е₂ = 0.

Часто используют другую формулировку второго закона Кирхгофа: алгебраическая сумма падений напряжений на элементах контура равна алгебраической сумме источников ЭДС, входящих в контур ,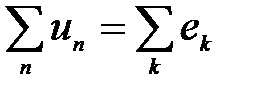

где n – номер пассивного элемента контура, k - номер активного элемента контура. Для схемы на рис. 1.6 второй закон Кирхгофа по второй форме записи имеет вид:

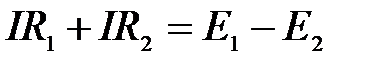
§ 16.Преобразование соединения ″треугольник″ в эквивалентную ″звезду″.

Рассмотрим преобразование треугольника в звезду.

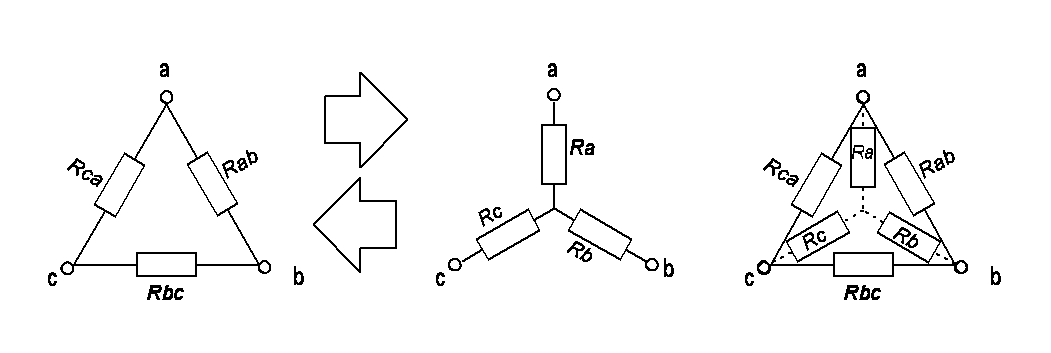
По второму закону Кирхгофа для треугольника:

R_abI_ab+ R_bcI_bc+ R_ca I_ca=0 (1)

Для узлов а и b: I_ca= I_ab–I_a; и I_bc= I_ab+I_b

Подставим в (1):

R_abI_ab+ R_bcI_ab+ R_bcI_b+ R_caI_ab– R_caI_a=0

I_ab(R_ab+ R_bc+ R_cа) + R_bcI_b– R_caI_a=0

;

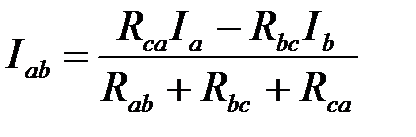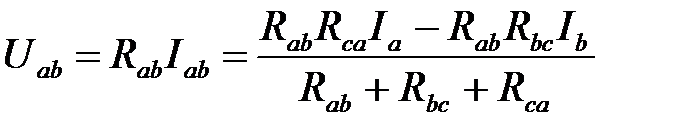
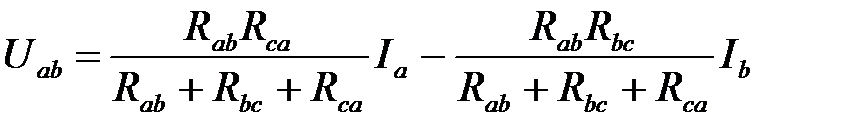(2)

Для звезды U_ab равно разности падений напряжений на R_a и R_b

U_ab= R_a I_a – R_b I_b (3)

Сравним с (2):

;

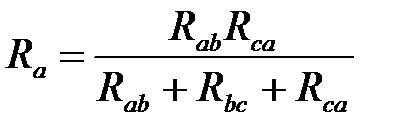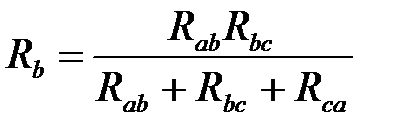
По аналогии запишем для R_c: .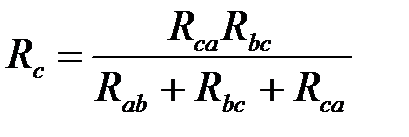

Сопротивление одной стороны треугольника равно дроби, в числителе которой произведение двух прилегающих к лучу сопротивлений, в знаменателе сумма всех сопротивлений.

Формулы обратного преобразования (звезды в треугольник) можно получить, заменив все сопротивления проводимостями:

; ;

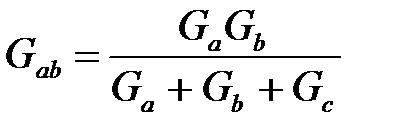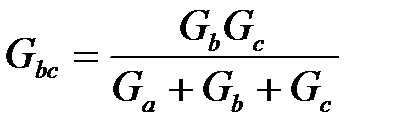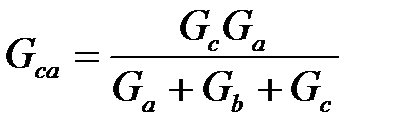
Сопротивления эквивалентного треугольника для заданных сопротивлений элементов звезды определяются из соотношений

; ; ,

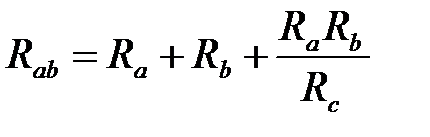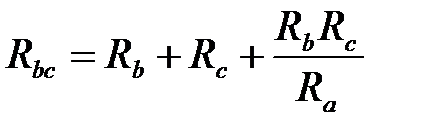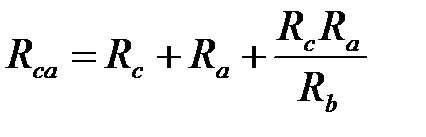Применение преобразования треугольника в звезду для схемы измерительного моста дает схему, в которой присутствуют только последовательные и параллельное соединения участков.