Силы отталкивания, действующие между атомами и молекулами на малых расстояниях
Нехимическое (физическое) взаимодействие атомов и молекул
Возникновение химической связи между атомами связано с перестройкой их внешних (валентных) оболочек и с перераспределением электронной плотности в пространстве, окружающем атомные ядра (приложение 3). При этом для образования химической связи необходимо выполнение следующих условий:
1) атомы должны так сильно сблизиться друг с другом, чтобы их электронные облака начали перекрываться;
2) атомы должны находиться друг возле друга достаточно долго для того, чтобы их внешние электронные оболочки успели перестроиться; другими словами, время взаимодействия атомов должно быть больше характерного времени образования химической связи;
3) энергия относительного движения атомных ядер должна быть меньше характерной энергии связи (в противном случае образовавшаяся связь может «разорваться»);
4) атомы должны иметь незаполненные электронные оболочки, которые содержат неспаренные электроны.
В том случае, если хотя бы одно из этих условий не выполняется, химическая связь между атомами не возникает. Однако это не означает, что атомы при этом никак не взаимодействуют друг с другом. Силы электромагнитной природы, которые действуют между атомами и молекулами, но не связаны с глубокой перестройкой их электронных орбиталей, мы будем называть нехимическими силами, или физическим взаимодействием атомов или молекул.
Силы отталкивания, действующие между атомами и молекулами на малых расстояниях
Даже силами химической природы, которые начинают действовать между атомами при образовании химической связи, невозможно объяснить тот факт, что атомные ядра внутри молекулы находятся на некотором равновесном расстоянии друг от друга. Силы химической связи имеют характер притяжения, поэтому для того, чтобы ядра находились в состоянии равновесия, между ними должны действовать еще и силы отталкивания, возникающие при достаточно сильном сближении атомов.
Природа этих сил становится ясна, если вспомнить, что атомные ядра, а также окутывающие их электронные облака имеют одноименные заряды. Такие заряды, как известно, должны отталкиваться друг от друга. А в случае сближения атомов с заполненными электронными оболочками на малых расстояниях между ними возникает дополнительное отталкивание, обусловленное принципом Паули.
В силу принципа запрета Паули два электрона с одинаково направленными спинами не могут находиться в одном и том же квантовом состоянии. Однако, когда электронные облака двух атомов перекрываются, электроны одного атома имеют тенденцию занимать те состояния, которые уже заняты электронами другого атома. Поэтому заполненные электронные оболочки могут перекрываться только в том случае, если этот процесс сопровождается частичным переходом электронов в свободные квантовые состояния с более высокой энергией. Увеличение энергии сближаемых атомов как раз и говорит о том, что между ними действуют силы отталкивания.
Таким образом, возникновение сил отталкивания между атомами (а также между молекулами, которые из них состоят) обусловлено отталкиванием атомных ядер и отталкиванием электронов, которые находятся на внешних (в случае молекул) или внутренних (в случае атомов внутри молекулы) оболочках.
Рассмотрим в качестве примера отталкивание, которое возникает при сближении двух атомов водорода (в этом случае отталкивание, обусловленное действием принципа Паули, можно не учитывать).
Если атом водорода находится в основном состоянии, то точное решение уравнения Шредингера, определяющее волновую функцию атомного электрона, будет иметь вид (приложение 1):
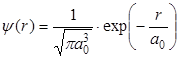 , , | (3.1) |
где r – расстояние до атомного ядра, 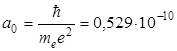 м – радиус первой боровской орбиты электрона в атоме водорода (боровский радиус), h – постоянная Планка, e и me – соответственно заряд и масса электрона.
м – радиус первой боровской орбиты электрона в атоме водорода (боровский радиус), h – постоянная Планка, e и me – соответственно заряд и масса электрона.
Плотность вероятности отыскания электрона на расстоянии r от атомного ядра задается квадратом волновой функции (3.1):
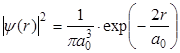 , , | (3.2) |
При этом плотность распределения заряда внутри атома водорода (e>0)
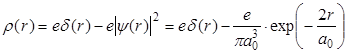 . . | (3.3) |
Первое слагаемое в этом выражении представляет собой плотность заряда ядра. Считая ядро точечным, легко сделать вывод, что эта плотность равна нулю везде, кроме той точки, в которой расположено ядро. В самой этой точке плотность заряда ядра +e/Ve ® ¥, так как объем точечного ядра Ve стремится к нулю. Таким образом, плотность заряда ядра действительно можно представить в виде +ed(r), где d(r) – так называемая дельта-функция Дирака:
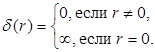
Второе слагаемое в выражении (3.3) представляет собой плотность заряда электрона, «размазанного» вокруг атомного ядра с «плотностью» (3.2).
Плотность распределения заряда (3.3) внутри атома водорода позволяет рассчитать потенциал его электрического поля.
Для этого следует решить уравнение Пуассона
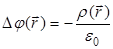 , , | (3.4) |
которое для атома водорода приобретает вид
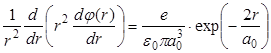 . . | (3.5) |
Точное решение этого уравнения, которое обращается в ноль при r®¥ и переходит в потенциал точечного ядра при r®0, определяется выражением:
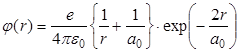 . . | (3.6) |
Полученная формула показывает, что на расстояниях r >> a0 электрическое поле атома водорода экспоненциально мало:
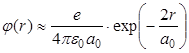 . . | (3.7) |
Поэтому взаимодействием между двумя атомами водорода, которые находятся на расстоянии R >> 2a0 можно пренебречь (рис.3.1, а).
В области r < a0 потенциал поля атома водорода представляет собой потенциал электрического поля атомного ядра, экранированного полем электрона:
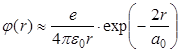 . . | (3.8) |
Поэтому при сближении двух атомов водорода до расстояний a0< R < 2a0, при которых начинают перекрываться волновые функции их валентных электронов (рис.3.1, б), возникает ситуация, благоприятная для образования химической связи (атомные электроны начинают притягиваться к ядрам соседних атомов). Однако при дальнейшем сближении атомов (при R < a0) в поле (3.8) ядра одного атома попадает ядро другого атома (рис.3.1, в). Поэтому между ядрами начинают действовать силы отталкивания. При этом энергия этого отталкивания
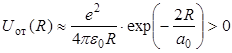 . . | (3.9) |
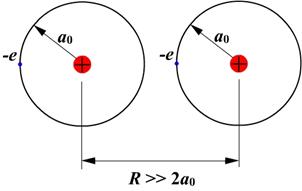 а) а) | 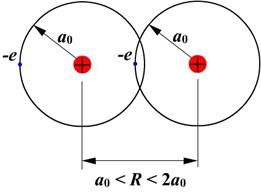 б) б) |
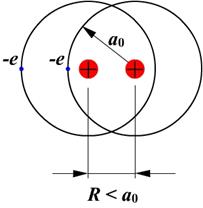 в) в) | Рис. 3.1.Взаимодействие атомов водорода: а) при R >> 2a0 атомы практически не взаимодействуют друг с другом; энергия их взаимодействия 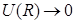 ; б) при a0< R < 2a0 атомы притягиваются друг к другу за счет притяжения атомных электронов к ядрам соседних атомов; ; б) при a0< R < 2a0 атомы притягиваются друг к другу за счет притяжения атомных электронов к ядрам соседних атомов; 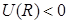 , возникает ситуация, благоприятная для образования химической связи; в) при R < a0 атомы отталкиваются друг от друга за счет электростатического отталкивания атомных ядер; , возникает ситуация, благоприятная для образования химической связи; в) при R < a0 атомы отталкиваются друг от друга за счет электростатического отталкивания атомных ядер; 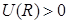 . . |
Энергию электростатического взаимодействия двух атомов водорода в диапазоне всех возможных значений межъядерного расстояния R можно рассчитать, зная распределение (3.6) потенциала электрического поля, создаваемого одним атомом, и распределение (3.3) плотности заряда в другом атоме:
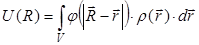 . . | (3.10) |
Однако аналитически интегрирование (3.10) может быть выполнено только в случае атомов водорода (при этом следует помнить, что рассматриваемая теория не учитывает принципа Паули, т.е. наличия у электронов спина). При расчете энергии взаимодействия многоэлектронных атомов для этого приходится использовать численные методы интегрирования.
В случае многоэлектронных атомов ситуация еще более усугубляется тем, что для таких атомов, как известно, не существует точного решения уравнения Шредингера. Поэтому различного рода приближенные или численные методы приходится использовать уже для расчета атомных потенциалов.
Среди приближенных методов вычисления атомных потенциалов наибольшее распространение получили метод самосогласованного поля Хартри-Фока и статистический метод Томаса-Ферми (приложение 2).
В методе Хартри-Фока волновая функция многоэлектронного атома, которая позволяет, как мы видели, рассчитать потенциал его электрического поля, представляется как суперпозиция волновых функций отдельных электронов. При этом предполагается, что каждый электрон движется в некотором эффективном (самосогласованном) поле, создаваемом атомным ядром и остальными электронами. Уравнение Шредингера для такой системы решается численно, методом последовательных приближений.
Подобная задача вполне под силу современным вычислительным машинам. Тем не менее метод последовательных приближений требует больших затрат машинного времени и может привести к большим численным ошибкам, которые накапливаются в процессе вычислений. Поэтому на практике метод Хартри-Фока обычно используется для описания состояния атомов, содержащих небольшое число электронов. Для описания сложных атомов с большим зарядовым числом Z обычно применяется статистический метод Томаса-Ферми.
В модели Томаса-Ферми не учитывается оболочечная структура атомов. Атом представляется в виде неподвижного положительно заряженного атомного ядра, вокруг которого случайным образом, но в соответствии с принципом Паули располагаются атомные электроны. Плотность такого электронного облака неоднородна: она определяется распределением потенциала электрического поля в атоме. В свою очередь, это распределение поля определяется распределением электронов в окружающем ядро пространстве.
Использование статистических методов дает возможность выразить плотность распределения заряда внутри атома Томаса-Ферми через распределение потенциала электрического поля. А решение уравнения Пуассона (3.4) позволяет представить потенциал электрического поля многоэлектронного атома в виде:
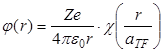 , , | (3.11) |
где c(x) – так называемая функция экранирования Томаса-Ферми, а aTF – длина экранирования Томаса-Ферми, имеющая смысл характерного расстояния от атомного ядра, на котором потенциал (3.11) убывает практически до нуля за счет экранирования электрического поля ядра атомными электронами:
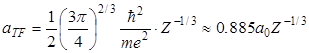 . . | (3.12) |
(Отметим аналогию между выражением (3.11) и (3.8). В формуле (3.8) Z = 1, 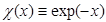 , а
, а 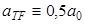 .)
.)
Функция экранирования c(x) в модели Томаса-Ферми рассчитывается численными методами. Однако она оказывается универсальной, не зависящей от сорта атомов функцией и допускает аналитическую аппроксимацию.
В качестве примера можно привести аппроксимацию, предложенную Мольер:
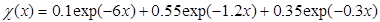 , , | (3.13) |
а также аппроксимацию, предложенную Линдхардом:
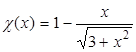 . . | (3.14) |
Функцию экранирования Томаса-Ферми, записанную в виде (3.13), часто называют функцией экранирования Мольер, функцию экранирования в форме (3.14) – функцией экранирования Линдхарда. Разлагая последнее выражение в области малых x в ряд, легко показать, что оно с хорошей точностью аппроксимирует выражение 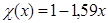 , которое в модели Томаса-Ферми является точным при x ® 0.
, которое в модели Томаса-Ферми является точным при x ® 0.
Вычисление энергии отталкивания атомов и в модели Хартри-Фока, и в модели Томаса-Ферми сводится к численному интегрированию выражения (3.10). Фирсов, однако, показал, что теория хорошо описывает экспериментальные данные, если в качестве выражения для потенциальной энергии отталкивания использовать функцию вида
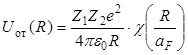 , , | (3.15) |
которая аналогична функции (3.9) и имеет смысл энергии кулоновского отталкивания атомных ядер с зарядами +Z1e и +Z2e, экранированных атомными электронами.
Функция c(x), которая входит в формулу (3.15), имеет тот же смысл (и вид), что и в выражении (3.11). Однако благодаря дополнительному экранированию ядра второго атома электронами его внутренних оболочек энергия отталкивания атомов (3.15) уменьшается с увеличением расстояния быстрее, чем электрическое поле (3.11), создаваемое первым атомом. Поэтому длина экранирования aF в выражении (3.15), оказывается меньше длины экранирования aTF (3.12):
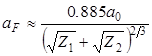 . . | (3.16) |
Очень часто при решении различного рода задач можно считать, что энергия отталкивания уменьшается до нуля мгновенно и достигает очень большой величины только в том случае, если расстояние между атомными ядрами становится меньше суммы R1 + R2 радиусов взаимодействующих атомов (см. табл.1.3):
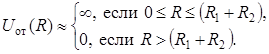 , , | (3.15) |
Такое приближение в описании взаимодействия атомов на малых расстояниях называется моделью жестких шаров.
