Магнитное поле движущегося заряда. Ганс Христиан Эрстед обнаружил, что магнитная стрелка
Ганс Христиан Эрстед обнаружил, что магнитная стрелка, помещенная вблизи, параллельно проводнику при включении тока отклоняется от своего первоначального направления. То есть вокруг проводника с током возникло магнитное поле, которое стало действовать на магнитную стрелку.
В 1826 г. Андре Мари Ампер выдвинул гипотезу, согласно которой вообще не существует магнетизма не связанного с движением электрических зарядов. Подобно тому, как в пространстве, в котором находятся электрические заряды, возникает электростатическое поле, так и в пространстве вокруг движущихся зарядов, а, следовательно, и вокруг проводника с током возникает магнитное поле. То есть вокруг движущегося заряда существуют и электрическое и магнитное поля — единое электромагнитное поле.
По современным представлениям магнитное поле обуславливается релятивистскими свойствами пространства и времени. Между неподвижными зарядами возникает только сила кулоновского взаимодействия. Если заряды привести в движение, помимо кулоновской силы возникнет дополнительная сила, называемая магнитной силой, которая связана с электрической силой соотношением  , где
, где 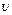 — скорость движения зарядов, c — скорость света.
— скорость движения зарядов, c — скорость света.
Эта сила описывается величиной второго порядка малости по величине  относительно кулоновского взаимодействия и сравнима с кулоновской силой при достаточно больших скоростях заряженных частиц.
относительно кулоновского взаимодействия и сравнима с кулоновской силой при достаточно больших скоростях заряженных частиц.
Магнитная сила заметна и при малых скоростях зарядов, если кулоновское (электрическое) взаимодействие по каким-то причинам не проявляется. Например, электрический ток в проводнике. Магнитное поле создается огромным числом, направленно движущихся зарядов, а электрическое поле этих зарядов нейтрализуется полем других зарядов, противоположного знака, например ионами кристаллической решетки.
Из теории относительности Эйнштейна следует, что всякий движущийся заряд создает вокруг себя магнитное поле, Индукция этого поля определяется выражением:
 ,
,
где  Гн/м — магнитная постоянная,
Гн/м — магнитная постоянная, 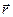 — радиус-вектор, проведенный от заряда до точки поля.
— радиус-вектор, проведенный от заряда до точки поля.
Направление вектора  определяется правилом векторного произведения — правила буравчика. Острие буравчика направляют вдоль вектора
определяется правилом векторного произведения — правила буравчика. Острие буравчика направляют вдоль вектора 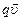 , рукоятку вдоль радиус-вектора
, рукоятку вдоль радиус-вектора 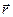 , тогда направление движения конца рукоятки при правовинтовом вращении укажет на направление вектора
, тогда направление движения конца рукоятки при правовинтовом вращении укажет на направление вектора  . Модуль вектора
. Модуль вектора  будет равен
будет равен
 ,
,
где 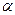 — угол между векторами
— угол между векторами 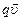 и
и 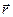 , r — модуль радиус-вектора
, r — модуль радиус-вектора 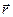 .
.
Сила Ампера
На проводник с электрическим током в магнитном поле, действует сила, называемая силой Ампера. Сила Ампера 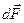 , приложенная к малому элементу проводника длины
, приложенная к малому элементу проводника длины 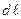 , с током силы I, создается силами Лоренца, которые действуют на движущие в проводнике носители тока. Пусть
, с током силы I, создается силами Лоренца, которые действуют на движущие в проводнике носители тока. Пусть  — объем элемента проводника, тогда число носителей тока в нем
— объем элемента проводника, тогда число носителей тока в нем  , где
, где  — концентрация носителей тока. Если
— концентрация носителей тока. Если  — средняя скорость упорядоченного движения носителей тока, а
— средняя скорость упорядоченного движения носителей тока, а 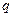 — заряд одного носителя, тогда сила Ампера, действующая на элемент проводника, будет равна
— заряд одного носителя, тогда сила Ампера, действующая на элемент проводника, будет равна  . Учитывая, что
. Учитывая, что  — плотность тока получим закон Ампера
— плотность тока получим закон Ампера
 .
.
Вектор  называют объемным элементом тока. Если же ток течет по тонкому проводу, то он называется линейным. Из-за малости площади поперечного сечения проводника
называют объемным элементом тока. Если же ток течет по тонкому проводу, то он называется линейным. Из-за малости площади поперечного сечения проводника 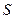 можно считать, что плотность
можно считать, что плотность  тока постоянна,
тока постоянна,  , и, следовательно,
, и, следовательно,  . Вектор
. Вектор 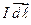 называют линейным элементом тока. Вектор
называют линейным элементом тока. Вектор  совпадает по направлению с вектором плотности тока. Тогда закон Ампера для линейного тока принимает вид
совпадает по направлению с вектором плотности тока. Тогда закон Ампера для линейного тока принимает вид
 .
.
Сила Ампера, действующая в магнитном поле на проводник конечной длины с током 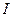 , равна
, равна
 .
.
В частности, если поле однородно, а проводник прямолинейный, то
 .
.
Направление силы 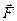 можно найти по правилу левой руки: если расположить ладонь левой руки так, чтобы вектор
можно найти по правилу левой руки: если расположить ладонь левой руки так, чтобы вектор  входил в ладонь, а четыре вытянутых пальца совпадали с направлением электрического тока в проводнике, то отставленный большой палец укажет направление силы Ампера. По модулю сила Ампера будет равна
входил в ладонь, а четыре вытянутых пальца совпадали с направлением электрического тока в проводнике, то отставленный большой палец укажет направление силы Ампера. По модулю сила Ампера будет равна
 ,
,
где 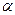 — угол между направлением тока (вектором плотности тока) в проводнике и вектором
— угол между направлением тока (вектором плотности тока) в проводнике и вектором  .
.
Из закона Ампера следует, что сила 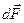 максимальна, если проводник с током расположен перпендикулярно к магнитному полю, тогда модуль вектора индукции
максимальна, если проводник с током расположен перпендикулярно к магнитному полю, тогда модуль вектора индукции  :
:
 .
.
Магнитная индукция 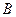 численно равна отношению максимальной силы, действующей со стороны магнитного поля на малый элемент проводника с током, к произведению силы тока на длину этого элемента. Направлен вектор
численно равна отношению максимальной силы, действующей со стороны магнитного поля на малый элемент проводника с током, к произведению силы тока на длину этого элемента. Направлен вектор  так, что
так, что  ,
,  , и
, и  образуют правовинтовую тройку.
образуют правовинтовую тройку.
