Физика колебаний и волн
Механические колебания.
Амплитуда, циклическая частота, фаза гармонических колебаний. Гармонический осциллятор. Пружинный маятник. Физический маятник. Математический маятник. Сложение колебаний. Затухающие колебания. Декремент колебания. Добротность колебательной системы. Вынужденные колебания под действием синусоидальной силы. Резонанс. Резонансные кривые.
Электромагнитные колебания.
Колебательный контур. Формула Томсона. Переменный ток. Дифференциальное уравнение затухающих колебаний и его решение. Коэффициент затухания, логарифмический декремент. Добротность. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Амплитуда и фаза при вынужденных колебаниях.
Волны.
Волновые процессы. Продольные поперечные волны. Длина волны, волновое число, фазовая скорость. Фронт волны. Волновая поверхность. Плоская волна. Бегущая волна. Сферическая волна. Стоячие волны. Электромагнитные волны. Волновое уравнение. Скорость распространения электромагнитных волн. Поляризация волн.
Оптика
Геометрическая оптика.
Элементы геометрической оптики. Законы геометрической оптики. Явление полного отражения. Линза. Формула тонкой линзы.
Волновая оптика.
Свет как электромагнитная волна. Когерентность и монохроматичность световых волн. Интерференционное поле от двух точечных источников. Опыт Юнга. Интерферометр Майкельсона. Интерференция в тонких пленках. Многолучевая интерференция.
Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Дифракция на одной щели. Дифракционная решетка. Дифракция Фраунгофера. Понятие о голографии. Распространение света в веществе. Дисперсия света. Поляризация света. Естественный и поляризованный свет. Поляризация света при его отражении и преломлении. Закон Брюстера. Двойное лучепреломление.
Квантовая физика
Физика атома, атомного ядра и элементарных частиц
Квантовая природа излучения.
Тепловое излучение и его характеристики. Законы Кирхгофа. Законы Стефана-Больцмана и смещения Вина. Формулы Рэлея-Джинса и Планка. Внешний фотоэффект. Уравнение Эйнштейна для внешнего фотоэффекта. Масса и импульс фотона. Давление света. Эффект Комптона. Диалектическое единство корпускулярных и волновых свойств электромагнитного излучения.
Физические модели атомов.
Модели атома Томсона и Резерфорда. Линейчатый спектр атома водорода. Эмпирические закономерности в атомных спектрах. Формула Бальмера.
Теория атома водорода по Бору. Постулаты Бора. Теория водородоподобного атома.
Квантовая природа вещества.
Элементы квантовой механики. Корпускулярно-волновой дуализм свойств вещества. Гипотеза де Бройля. Опыты Дэвиссона и Джермера. Дифракция микрочастиц. Принцип неопределенности Гейзенберга. Волновая функция, ее статистический смысл и условия, которым она должна удовлетворять. Уравнение Шредингера. Квантовая частица в одномерной потенциальной яме. Одномерный потенциальный порог и барьер. Линейный гармонический осциллятор в квантовой механике.
Физика атомов и молекул.
Элементы современной физики атомов и молекул. Стационарное уравнение Шредингера для атома водорода. Волновые функции и квантовые числа. Правила отбора для квантовых переходов. Опыт Штерна и Герлаха. Эффект Зеемана.
Принцип Паули. Молекулярные спектры.
Оптические квантовые генераторы
Спонтанное и индуцированное излучение. Инверсное заселение уровней активной среды. Основные компоненты лазера. Условие усиления и генерации света. Особенности лазерного излучения. Основные типы лазеров и их применение.
Физика атомного ядра и элементарных частиц.
Строение и свойства атомных ядер. Состав ядра. Изотопы. Масса и энергия связи в ядре. Радиоактивность. Ядерные реакции. Явление радиоактивности. Закон радиоактивного распада. Период полураспада. Понятие о ядерных реакциях. Законы сохранения в ядерных реакциях.
Современная физическая картина мира.
Иерархия строения материи. Эволюция Вселенной. Физическая картина мира как философская категория.
ПРИМЕРЫ ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
ВАРИАНТ 1
Задача №1
В подвешенный на нити длиной 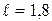 м деревянный шар массой
м деревянный шар массой 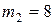 кг попадает горизонтально летящая пуля массой
кг попадает горизонтально летящая пуля массой 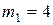 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол
г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол 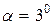 ? Размером шара пренебречь. Удар пули считать прямым центральным.
? Размером шара пренебречь. Удар пули считать прямым центральным.
Дано: 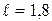 м м 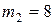 кг кг 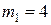 г = 0,004 кг г = 0,004 кг 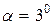 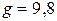 м/с2 м/с2 | Анализ: В задаче следует рассмотреть процесс неупругого соударения двух тел. В соответствии с условием задачи два сталкивающихся тела в момент соударения можно рассматривать как замкнутую механическую систему, т.к. внутренние силы много больше внешних. По условию задачи удар прямой, центральный и неупругий, что дает возможность рассматривать движение тел после |
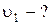 |
столкновения как движение материальной точки с массой 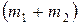 .
.
 |
Решение:
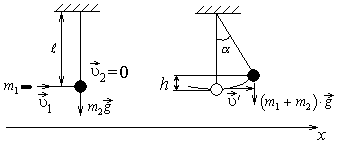
Запишем закон сохранения импульса для системы тел 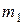 и
и 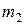 :
:
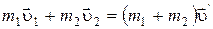 ,
,
где 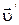 – общая скорость шара и пули после неупругого удара.
– общая скорость шара и пули после неупругого удара.
В проекции на ось x имеем:
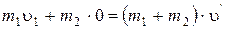 . (1)
. (1)
Уравнение (1) позволяет выразить искомую величину 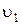 через
через 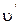 , которая в свою очередь может быть найдена на основании закона сохранения энергии в применении к системе
, которая в свою очередь может быть найдена на основании закона сохранения энергии в применении к системе 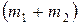 после ее формирования, т.е. после неупругого столкновения.
после ее формирования, т.е. после неупругого столкновения.
Итак, из уравнения (1) имеем:
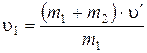 (2)
(2)
Запишем закон сохранения энергии для системы тел после неупругого соударения (полная механическая энергия остается величиной постоянной):
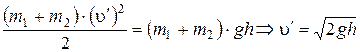 .
.
Величина 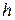 может быть найдена из геометрических соображений:
может быть найдена из геометрических соображений:
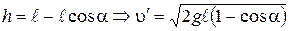 . (3)
. (3)
Подставляя (3) в (2), получаем
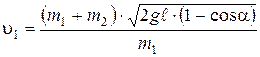 .
.
Проверка размерности:
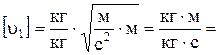 м/с.
м/с.
Выполняем расчет:
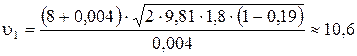 (м/с).
(м/с).
Ответ: 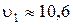 м/с.
м/с.
Задача №2
Смесь водорода и азота общей массой 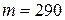 г при температуре T = 600 К и давлении p = 2,46 МПа занимает объем V = 30 л. Определить массу m1 водорода и массу m2 азота.
г при температуре T = 600 К и давлении p = 2,46 МПа занимает объем V = 30 л. Определить массу m1 водорода и массу m2 азота.
Дано: m = 290 г = 29×10-2 кг T = 600 К= 6×102 К р = 2,46 МПа = 2,46×106 Па V = 30 л = 3×10-2 м3 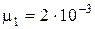 кг/моль кг/моль 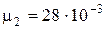 кг/моль кг/моль | Анализ: Водород и азот – химически невзаимодействующие газы, поэтому состояние их смеси может быть рассмотрено с позиции закона Дальтона: давление смеси химических невзаимодействующих газов равно сумме парциальных давлений компонентов. 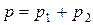 (1) (1) |
| m1 (H2) (водород) –? m2 (N2) (азот) –? |
Решение:
Для определения парциального давления запишем уравнение Менделеева – Клапейрона для каждого компонента:
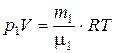 , (2)
, (2)
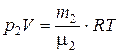 , (3)
, (3)
где индексом “1” отмечены характеристики, относящиеся к водороду, а индексом “2” – к азоту. Выразим 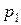 и
и 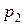 из уравнений (2) и (3) и подставим в закон Дальтона (1):
из уравнений (2) и (3) и подставим в закон Дальтона (1):
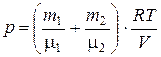 ; (4)
; (4)
при этом 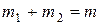 . (5)
. (5)
Из (4) и (5) следует
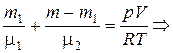
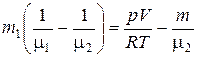 . (6)
. (6)
Из (6) получаем
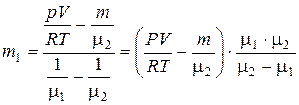 . (7)
. (7)
И далее находим массу азота:
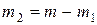 .
.
Проверка размерности:
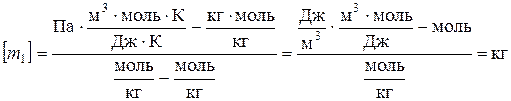 .
.
Расчет:
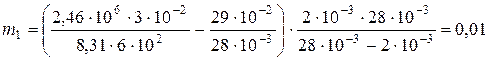 (кг)
(кг)
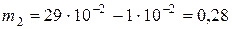 (кг)
(кг)
Ответ: 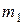 = 0,01 кг,
= 0,01 кг, 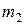 = 0,28 кг.
= 0,28 кг.
Задача №3
Две 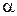 –частицы, находясь первоначально достаточно далеко друг от друга, движутся по одной прямой навстречу одна другой со скоростями
–частицы, находясь первоначально достаточно далеко друг от друга, движутся по одной прямой навстречу одна другой со скоростями 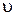 и 2
и 2 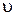 соответственно. На какое наименьшее расстояние они могут сблизиться?
соответственно. На какое наименьшее расстояние они могут сблизиться?
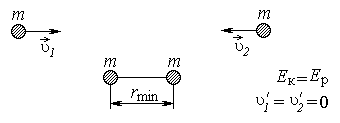
Дано: m1 = m2 = m = 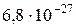 кг q1 = q 2 = q = кг q1 = q 2 = q = 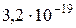 Кл Кл 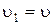 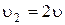 | Анализ: По условию задачи движение частиц задано в лабораторной системе отчета. Однако удобнее было бы рассматривать движение частиц в системе центра масс, движущейся относительно лабораторной со скоростью 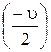 , направленной влево. В этой системе отсчета скорости частиц будут , направленной влево. В этой системе отсчета скорости частиц будут |
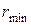 -? -? |
противоположны по направлению и равны по модулю 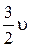 . В подобной ситуации (точнее, в этой системе отсчета) частицы в момент наибольшего сближения останавливаются и при этом их кинетическая энергия полностью переходит в потенциальную энергию электростатического взаимодействия.
. В подобной ситуации (точнее, в этой системе отсчета) частицы в момент наибольшего сближения останавливаются и при этом их кинетическая энергия полностью переходит в потенциальную энергию электростатического взаимодействия.
 |
Решение:
На основании закона сохранения энергии
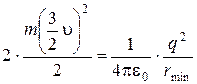 .
.
Отсюда
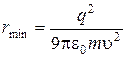 ,
,
где 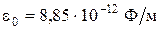 – электрическая постоянная.
– электрическая постоянная.
Проверка размерности:
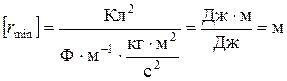 .
.
Ответ: 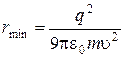 .
.
Задача №4
Тонкий провод в виде кольца массой 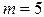 г свободно подвешен на неупругой нити в однородном магнитном поле. По кольцу течет ток силой i=6 А. Период Т малых крутильных колебаний относительно вертикальной оси равен 2,2 с. Найти индукцию В магнитного поля.
г свободно подвешен на неупругой нити в однородном магнитном поле. По кольцу течет ток силой i=6 А. Период Т малых крутильных колебаний относительно вертикальной оси равен 2,2 с. Найти индукцию В магнитного поля.
| Дано: m = 5 г = 0,005 кг = 5×10-3 кг i = 6 А; B = const T = 2,2 с | Анализ: Контур с током обладает системным магнитным моментом, вектор которого в состоянии устойчивого равновесия совпадает c направлением внешнего магнитного поля. |
| B –? |
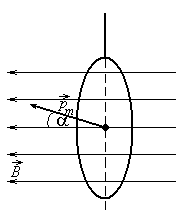 Если же вектор магнитного момента
Если же вектор магнитного момента 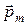 не совпадает с вектором
не совпадает с вектором 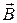 , то на контур действует возвращающий механический момент
, то на контур действует возвращающий механический момент 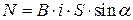 под действием которого контур будет совершать колебательные движения. (Здесь S – площадь, ограниченная контуром).
под действием которого контур будет совершать колебательные движения. (Здесь S – площадь, ограниченная контуром).
Решение:
Запишем уравнение движения кругового контура для случая малых колебаний:
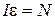 , (1)
, (1)
где 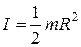 – момент инерции кольца относительности оси, лежащей в плоскости кольца и проходящей через его центр;
– момент инерции кольца относительности оси, лежащей в плоскости кольца и проходящей через его центр; 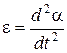 – угловое ускорение, N - возвращающий механический момент, равный
– угловое ускорение, N - возвращающий механический момент, равный 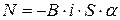 (при малых углах
(при малых углах 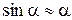 );
); 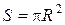 . Тогда уравнение (1) примет вид:
. Тогда уравнение (1) примет вид:
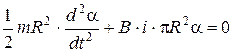 ;
;
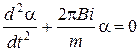 ;
;
Таким образом, мы получаем уравнение гармонических колебаний кольца для которых циклическая частота 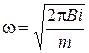 .
.
Учитывая связь периода колебаний и частоты, имеем:
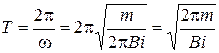 .
.
Отсюда
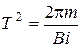 ,
,
следовательно,
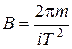 .
.
Проверка размерности:
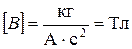 .
.
Расчет:
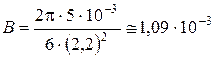 (Tл)
(Tл)
Ответ: 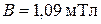 .
.
Задача №5
На дифракционную решетку нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в n = 4,6 раза больше длины световой волны. Найти общее число m дифракционных максимумов, которое теоретически возможно наблюдать в данном случае.
Дано: d = 4,6 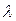 | Анализ: В задаче предлагается рассмотреть дифракцию нормально падающего на поверхность дифракционной решетки монохроматического пучка света. Общее число возможных дифракционных максимумов будет определяться наибольшим порядком наблюдаемого максимума. |
| m –? |
Решение:
Для решения задачи воспользуемся условием максимума дифракционной решетки. Разность хода лучей от соседних щелей должна быть равна целому числу длин волн.
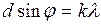 , (1)
, (1)
где k – порядок максимума.
Модуль 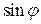 не может превысить единицу.
не может превысить единицу.
Поэтому из формулы (1) вытекает, что наибольший порядок наблюдаемого максимума kmax должен быть меньше отношения периода решетки d к длине волны λ
kmax < 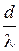 ;
;
следовательно,
kmax < 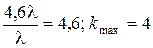 .
.
Общее количество максимумов будет равно сумме центрального максимума и числа максимумов справа и слева от центрального:
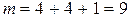 .
.
Ответ: 9 максимумов.
Задача №6
Параллельный пучок электронов, ускоренный напряжением 30 В, падает нормально на экран, в котором имеется щель шириной 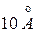 . За экраном, на расстоянии 0,1 м от него параллельно щели перемещается детектор очень малых размеров. Какова примерно ширина области, в которой детектор зарегистрирует электроны?
. За экраном, на расстоянии 0,1 м от него параллельно щели перемещается детектор очень малых размеров. Какова примерно ширина области, в которой детектор зарегистрирует электроны?
Дано: 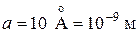 U = 30 B. U = 30 B. 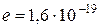 Кл – заряд электрона Кл – заряд электрона 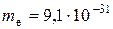 кг – масса электрона L = 0,1 м кг – масса электрона L = 0,1 м 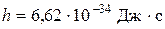 | АНАЛИЗ. В содержании задачи раскрывается мысленный (модельный) опыт Томсона по дифракции параллельного пучка электронов на щели. В ряде учебных пособий на анализе этого опыта делается вывод одного из центральных принципов неопределенности Гейзенберга 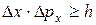 . . |
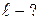 |
Решение:
Электрическое поле, совершая работу, равную 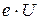 , сообщает электрону кинетическую энергию
, сообщает электрону кинетическую энергию 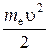 , т.е.
, т.е. 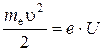 или
или 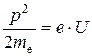 , где p – импульс электрона. Отсюда:
, где p – импульс электрона. Отсюда:
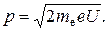
Движущийся электрон, как и любая другая микрочастица, обладает волновыми свойствами. Длина волны де Бройля 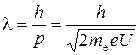 , где h – постоянная Планка.
, где h – постоянная Планка.
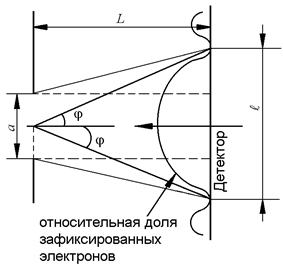
 Пучок электронов испытывает дифракцию на щели. Наиболее вероятная область локализации электрона может быть отнесена к центральному максимуму дифракционной картины, граница которого определится условием минимума первого порядка
Пучок электронов испытывает дифракцию на щели. Наиболее вероятная область локализации электрона может быть отнесена к центральному максимуму дифракционной картины, граница которого определится условием минимума первого порядка 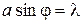 .
.
Из рисунка находим, полагая ввиду малости углов 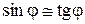 ,
, 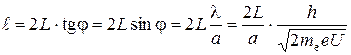
Проверка размерности:
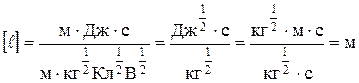 .
.
Расчет:
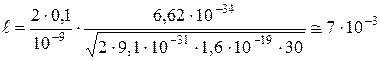 (м) = 0,7 (см).
(м) = 0,7 (см).
Обсуждение результата.
Приведенное решение соответствует классической ситуации, когда электрическое поле создает движение со скоростью 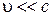 (скорости света). При напряжениях порядка
(скорости света). При напряжениях порядка 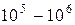 В необходимо перейти к соотношениям релятивистской динамики:
В необходимо перейти к соотношениям релятивистской динамики:
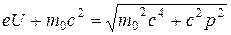 ,
,
и проводить анализ решения на основе этого соотношения.
Ответ: 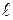 = 0,7 см.
= 0,7 см.
Используемая литература:
1. Савельев, И.В. Курс общей физики: В 3 т. [Текст]: Учебное пособие / И. В. Савельев.– Изд.5-е, стереотип. – СПб.: Изд-во “Лань”, 2006, Т.1- 496 с. – (Механика, колебания и волны, молекулярная физика).
2. Савельев, И.В. Курс общей физики: В 3 т. [Текст]: Учебное пособие / И. В. Савельев.– Изд.5-е, стереотип. – СПб.: Изд-во “Лань”, 2006, Т.2. - 496 с.- (Электричество и магнетизм. Волны. Оптика).
3. Савельев, И.В. Курс общей физики: В 3 [Текст]: Учебное пособие / И. В. Савельев. – Изд.5-е, стереотип. – СПб.: Изд-во “Лань”, 2006,т. - 2-е изд., испр. - М.: Наука, 1982. Т.3 - 304 с. (Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц)
4. Пиралишвили,Ш.А. Механика. Электромагнетизм. - [Текст]/ Ш.А.Пиралишвили, Н.А.Мочалова, З.В.Суворова, Е.В.Шалагина, В.В.Шувалов. –М.: Машиностроение, 2006. -336с.
5. Пиралишвили, Ш.А. Колебания. Волны. Геометрическая и волновая оптика. Квантовая и ядерная физика. .- [Текст]/ Ш.А.Пиралишвили, Н.А.Мочалова, З.В.Суворова, Е.В.Шалагина, В.В.Шувалов. –М.: Машиностроение-1, 2007. -341с.
6. Пиралишвили, Ш.А.Термодинамика и молекулярная физика. Элементы статистической физики. Элементы физики конденсированного состояния. - [Текст]/ Ш.А.Пиралишвили, Н.А.Каляева, З.В.Суворова, Е.В.Шалагина, В.В.Шувалов. –М.: Машиностроение-1, 2008. -348с.
