ТОК В МЕТАЛЛАХ, Основные ЖИДКОСТЯХ И ГАЗАХ ФОРМУЛЫ 2 страница

m,E,q О a=? z a

у E

g Tl

F хmg

Запишем условие равновесия шарика, например, через равенство нулю моментов сил, действующих на него относительно оси Z, проходящей через точку подвеса О перпендикулярно плоскости рисунка:

mql×sina = F ×lcosa,

где l – длина нити;

F = qE.

Следовательно, tga = qE; a= arctgqE.

ЗАДАЧА 3. Небольшой шарик массой m, имеющей заряд q, вращается в горизонтальной плоскости на непроводящей нити длиной l. Определить период обращения шарика, если в центре окружности, описы-ваемой шариком при вращении, расположен точечный заряд q. При вращении нить образует с вертикалью угол a.

Дано: Решение

q, a, m, l

T = ?

FK q q хmg

F=4pe0r2,где r = lsina.

По второму закону Ньютона:

T sina − FK= mv2 ;

T cosa −mg = 0.

2 2

= mg ×tga − ,

4 0l sin отсюда находим

V= lsina çmg×tga − q2 ÷.

è 4 0lsin ø

Следовательно, период обращения

T = 2 r = 2p×l×sina =

lsina æ q2 ö

m ç 4pe0l2 sin2 aø

= 2p l×sina .

2 g×tga−4pe0ml2 sin2 a

ЗАДАЧА 4. Три тонкие металлические пластины, имеющие заряды q, 3q, 2q, расположены параллельно друг другу. Площадь каждой пластины S. Найти силу, действующую на среднюю пластину. Электрическое поле, созданное каждой пластиной, считать однородным.

Дано: Решение

q, 3q, 2q, S q 3q 2q

E1F = ?

Сила, действующая на среднюю пластину с зарядом 3q, может определена по формуле F = 3qE,

где Е – напряженность электрического поля в месте расположения данной пластины, создаваемого крайни-ми пластинами. Если q > 0, то векторы напряженности электрических полей, создаваемых ими, будут на-правлены так, как показано на рисунке.

ТОК В МЕТАЛЛАХ, Основные ЖИДКОСТЯХ И ГАЗАХ ФОРМУЛЫ 2 страница - student2.ru

r r

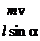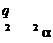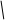
1=2e0=2e0S ;

s2 2q 2 2e0 2e0S

Следовательно, средняя пластина будет находиться в электрическом поле напряженностью E = E2− E = q и на нее будет действовать сила F =3qE = 3q2.

0 0

ЗАДАЧА 5. Точки А, В, С и D расположены на прямой и разделены равными промежутками l. В точке А помещен заряд q =8×10−12Кл, в точке В – заряд

q2= −5×10−12Кл. Какой заряд q3 поместить в точку D, чтобы напряженность 1 2 поля в точке С была равна нулю?

l D

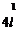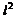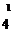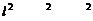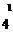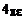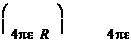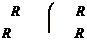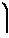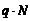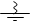
Дано:

1=8×10−12Кл q2= −5×10−12Кл

ЕС= 0

Решение

E = k q2, E2= k q2,

так как Е2 > Е1, то третий заряд должен быть отрицательным.

q3 = ? Е2 С Е1 Е3

ЕС= Е1 + Е3 – Е2,

0 = k 1+ k q3−k q2 или q+q3= q2,

4 l l т. е.

3= q2− q=5×10−12−2×10−12=3×10−12Кл.

ЗАДАЧА 6. Металлический шар радиусом R1, заряженный до потенциала f, окружают концентриче-ской сферической проводящей оболочкой радиусом R2.

Чему станет равен потенциал шара, если оболочку заземлить?

Дано: Решение f, R1, R2 –q

f0 = ? R1

+q R2

Потенциал сферической поверхности f = q , откуда q = f×4pe0R . 0 1

На поверхности шара радиусом R2 появится индуцированный заряд –q. По принципу суперпозиции полей

f = f+ç −q ÷ = f− f×4pe01= f 1− 1. è 0 2 ø 0 2 è 2 ø

ЗАДАЧА 7. Потенциал одной заряженной капли ртути равен f. Каким станет потенциал при слиянии N таких капель в одну большую?

Дано: Решение

N, f Потенциал маленькой капли:

f0 = ? f=4pe0r ,откуда q=f×4pe0r.

Потенциал большой капли:

f0=4pe0R ,

но масса большой капли M = N ×m, т. е. 4pR3 = N 4p×r3, тогда

R = r×3N.

f0 = N×f×4pe0r= f×N 2. 0

ЗАДАЧА 8. Какую минимальную работу нужно совершить, чтобы переместить заряд Q из точки В в точку С в поле двух точечных зарядов q1 и q2? Расстояния a, l, d известны.

Дано: Решение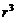
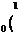
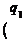