Законы Кеплера и элементы орбиты
В теории невозмущенного движения ИСЗ полагают, что спутник вращается вокруг сферической Земли с абсолютно равномерным распределением масс в ее теле, и сила притяжения между Землей и спутником является единственной причиной его орбитального движения. Всю массу Земли при этом можно считать сосредоточенной в центре масс и рассматривать движение спутника в гравитационном поле, создаваемом центром масс Земли. Спутник при этом рассматривают как материальную точку с единичной массой.
В этом случае движение ИСЗ по орбите описывается законами Кеплера, которые сформулируем применительно к движению спутников Земли.
Первый закон Кеплера. Спутник движется по эллипсу, в одном из фокусов которого находится центр масс Земли.
Второй закон Кеплера.Радиус-вектор спутника за равные промежутки времени описывает («заметает») равные площади.
Третий закон Кеплера.Квадраты периодов обращения любых двух спутников относятся как кубы больших полуосей их орбит.
Пусть точка М является фокусом, в котором находится центр масс Земли (рисунок 2). Точка П орбитального эллипса, ближайшая к фокусу М, называется перицентром.
 Рисунок 2 — Орбитальный эллипс. Рисунок 2 — Орбитальный эллипс. |
Точка А, наиболее удаленная от фокуса М называется апоцентром. Линия, соединяющая точки А и П, называется линией апсид, а сами точки А и П — апсидами.
Введем орбитальную систему координат Xw , Yw , Zw = 0, начало которой находится в точке М (центре масс), положительное направление оси Xw совпадает с направлением в перицентр.
Полярными координатами в орбитальной системе координат являются радиус-вектор 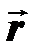 и истинная аномалия q. Радиус-вектор проводится из начала координат (точка М) до точки i орбиты, где находится ИСЗ в момент ti. Истинная аномалия q — это угол, отсчитываемый от оси Xw до радиус-вектора.
и истинная аномалия q. Радиус-вектор проводится из начала координат (точка М) до точки i орбиты, где находится ИСЗ в момент ti. Истинная аномалия q — это угол, отсчитываемый от оси Xw до радиус-вектора.
Уравнение эллипса в полярных координатах:
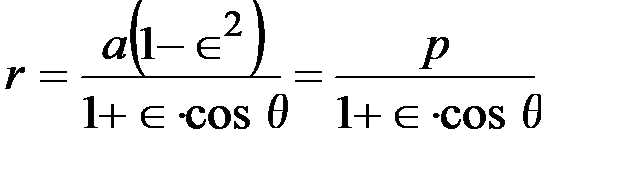 , (1.16)
, (1.16)
где a – большая полуось орбиты; 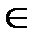 – эксцентриситет орбиты (эллипса);
– эксцентриситет орбиты (эллипса);
 – фокальный параметр.
– фокальный параметр.
Эксцентриситет является характеристикой вытянутости (сплюснутости) орбиты и равен:
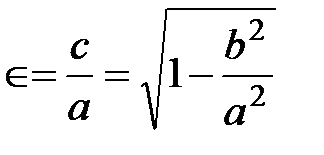 , (1.17)
, (1.17)
где a – расстояние между центром и фокусом эллипса; b – малая полуось эллипса.
Наряду с истинной аномалией q при описании движения спутников, планет и звезд используют эксцентрическую аномалию Е. Проведем из центра C эллипса окружность с радиусом, равным большой полуоси a эллипса. Из точки i орбиты опустим перпендикуляр 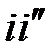 на линию апсид и продолжим его до пересечения с проведенной окружностью в точке
на линию апсид и продолжим его до пересечения с проведенной окружностью в точке 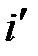 . Соединив точку
. Соединив точку 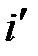 с точкой C, получим угол Е между направлением в перицентр и направлением на точку
с точкой C, получим угол Е между направлением в перицентр и направлением на точку 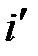 . Если взять эксцентрическую аномалию Е в качестве аргумента, то уравнение эллипса будет иметь вид:
. Если взять эксцентрическую аномалию Е в качестве аргумента, то уравнение эллипса будет иметь вид:
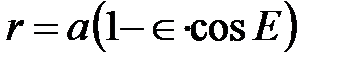 . (1.18)
. (1.18)
Следствием второго закона Кеплера является неравномерность движения спутника по орбите. Максимального значения орбитальная скорость 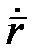 достигает в перицентре, а минимального — в апоцентре.
достигает в перицентре, а минимального — в апоцентре.
Следствием третьего закона Кеплера является формула для периода обращения ИСЗ:
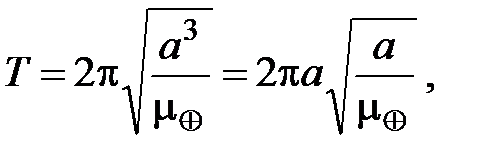 (1.19)
(1.19)
где mÅ — геоцентрическая гравитационная постоянная,
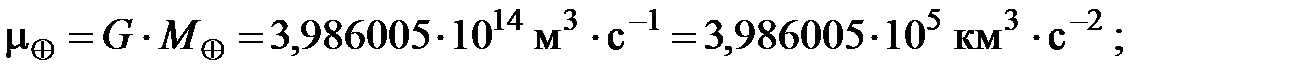
G = 6,67259·10–11 Н·м2·кг–2 — постоянная всемирного тяготения;
МÅ = 5,976·1024 кг — масса Земли.
Величина mÅ является одной из фундаментальных геофизических констант.
Ориентацию орбитальной плоскости в пространстве будем определять с помощью эйлеровых углов J, W, и w.
Наклонение орбиты J – угол между орбитальной плоскостью и плоскостью экватора. Угол J изменяется от 0° (ИСЗ движется по экватору с запада на восток) до 180° (ИСЗ движется в противоположном направлении).
Долгота восходящего узла W – угол между направлением от центра масс Земли на точку весеннего равноденствия и линией узлов (линией пересечения плоскости орбиты и плоскости экватора).
Угол w – аргумент перицентра – измеряется от положительного направления линии узлов OW до линии апсид OP (рисунок 3).
Углы J, W, w называются эйлеровыми углами, определяющими ориентацию орбитальной системы координат относительно геоцентрической системы координат.
Часто вводят также угол U:
U = w + q, (1.20)
который называют аргументом широты.
Рассмотрим рисунок 3. Здесь обозначены:
Oxyz– геоцентрическая инерциальная система координат;
OXYZ– гринвичская геоцентрическая система координат, которая вращается вместе с Землей вокруг оси OZ, делая один оборот за одни звездные сутки;
Si– звездное время в Гринвиче, равное углу между осями Ox и OX в момент ti;
точка W – восходящий узел орбиты ИСЗ, который является точкой пересечения экватора и орбиты при движении ИСЗ из южного полушария в северное;
OW – положительное направление линии узлов, по которой пересекаются плоскость орбиты и плоскость земного экватора;
i – положение ИСЗ на орбите в момент фотографирования ti;
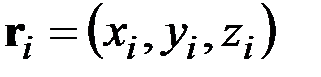 – геоцентрический радиус-вектор ИСЗ в момент фотографирования ti;
– геоцентрический радиус-вектор ИСЗ в момент фотографирования ti;
aiи di – геоцентрические прямое восхождение и склонение ИСЗ;
Угол W – долгота восходящего узла; угол между направлением оси Ox в точку весеннего равноденствия g и положительным направлением линии узлов OW;
Угол J – угол наклона (наклонение) плоскости орбиты к плоскости экватора;
Точка Pi – перицентр орбиты, точка орбиты, наиболее близко расположенная к центру масс Земли (фокусу орбитального эллипса);
Угол w – аргумент перицентра, отсчитываемый в плоскости орбиты от положительного направления линии узлов OW до направления OP в перицентр.
 Рисунок 3 — Орбита ИСЗ в гринвичской системе координат Рисунок 3 — Орбита ИСЗ в гринвичской системе координат |
Инерциальные геоцентрические координаты спутника выражаются через радиус-вектор r и эйлеровы углы следующими формулами:
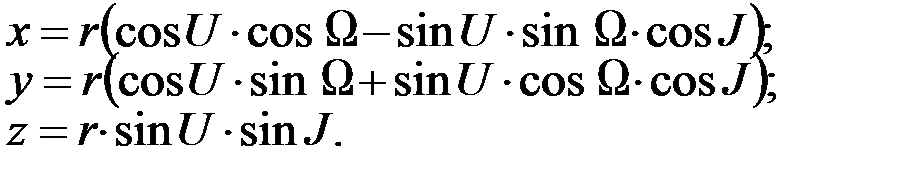 (1.21)
(1.21)
