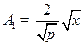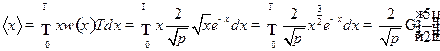Ферми и Бозе газы элементарных частиц

Элементарная частица – значит что квантовые частицы рассматриваются как точки, не учитывая их структуры. Исследуем только поступательное движение этих частиц. В этом и есть смысл слов «элементарная частица».

В этом случае можем воспользоваться квазиклассическим приближением.

Здесь переходим от 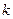- номера квантового состояния в фазовое пространство .

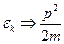
это в квазиклассике, когда .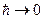

Состояние описывается фазовой точкой в фазовом пространстве. В фазовом пространстве имеем одну точку, т.к. состояние одночастичное.

В фазовом пространстве число частиц:

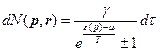
Пишем 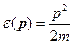, т.к. рассматриваем поступательное движение, т.е. следует зависимость только от 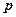, а от 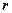нет зависимости, наша частица – как точка.

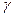- кратность вырождения по спину

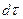- число одночастичных состояний в элементарном объёме фазового пространства.

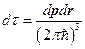
Поскольку энергия зависит только от 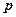, то можем проинтегрировать по 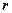и поставить объём :

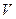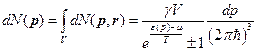
Отсюда можно посчитать полное число частиц в системе и полную энергию системы.

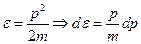(28)

с помощью этого соотношения преобразуем элементарный объём в импульсном пространстве, используя сферические координаты

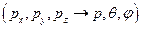
Так как функция, стоящая перед 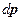не зависит от углов, а зависит только от модуля :

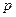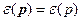
то можем проинтегрировать по углам. Учтем ещё, что:

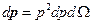
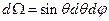
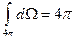
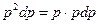
Используем (28):

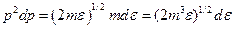
Значит:

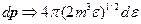
Тогда число частиц, приходящихся на единичный интервал энергии:

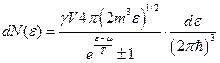
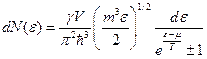
здесь «+» -для Ферми-Дирака, а «-» - для Бозе-Эйнштейна.

Посчитаем среднюю энергию системы и среднее число частиц.

При переходе в термодинамику для наблюдаемых величин пишем:

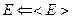и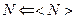

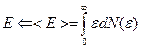
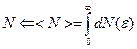
Среднюю энергию и среднее число частиц можно посчитать ещё и таким способом:

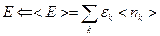- сумма по одночастичным состояниям

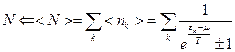
При переходе к квазиклассическому приближению имеем:

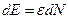
Точно так же рассчитывается термодинамический потенциал:

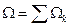
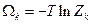, где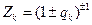

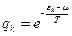
Поэтому при подстановке 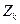в 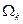имеем:

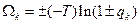
«+» -для Ферми-Дирака, а «-» - для Бозе-Эйнштейна.

В квазиклассическом приближении получим:

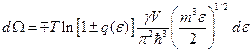
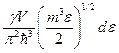- возникло при переходе к квазиклассике в переменные по энергии.

Здесь .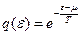

§28. Расчёт импульса Ферми для электронного газа при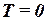

Будем пользоваться формулой: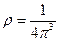

Запишем функцию Ферми для электронного газа:

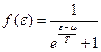- он здесь как функция энергии

И рассматривается случай, когда 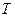очень близко к 0, :

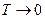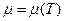
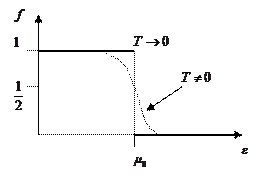, у нас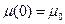

При малых 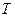показатель экспоненты отрицательный слева от 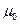и положительный справа от .

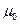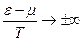, при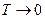

Тогда

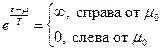
Поэтому:

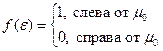
Видим, что 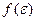имеет вид ступеньки: слева все уровни заселены, а справа все уровни свободны.

Химический потенциал определяется числом частиц в системе.

Можно писать

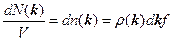
где 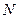- число частиц, а 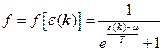- функция Ферми-Дирака, при 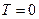она имеет вид ступеньки.

Запишем явный вид :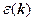

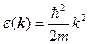
это выражение получается из выражения кинетической энергии электрона с импульсом :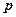

,

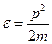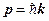
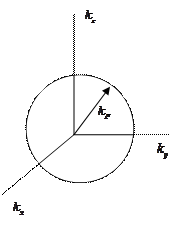
Тогда всё сводится к интегрированию в 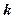-пространстве или в Фурье-пространстве. Размерность .

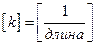Пределы интегрирования в 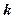-пространстве:

Это шар с радиусом, который определяется 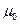. Радиус этого шара часто называют 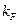, т.е. 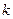-фермиевским.

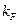определяется из 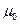, т.е. из числа частиц (электронов) в системе.

Полагаем объём 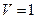и найдём полное число частиц в системе:

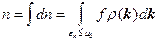
здесь из под интеграла убрали 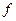, т.к. в этом пределе интегрирования 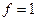, а вне этого предела 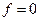и интеграл тоже равен нулю.

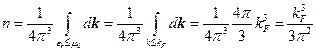
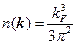
И тогда получаем:

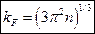
Импульс Ферми:

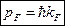
Найдём :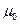

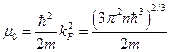
т.е. химический потенциал или уровень Ферми определяется концентрацией частиц.

§29. Расчёт энергии электронного газа при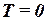

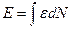
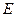- это полная энергия электронного газа.

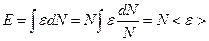
где 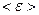- средняя энергия, приходящаяся на один электрон.

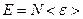
Энергия 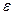имеет вид:

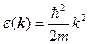
Тогда:

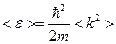
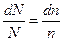
Найдём среднее :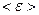

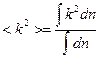
Учтём, что при 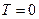область интегрирования является сферой, тогда:

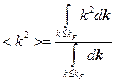
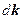- это элементарный объём в 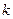-пространстве, т.е. скаляр, а не вектор.

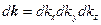
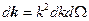
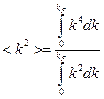
здесь мы уже сократили интегралы по углам, т.к. в числителе и в знаменателе они одинаковые: .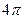

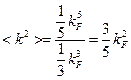
Но 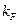определяет энергию Ферми:

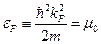
Значит:

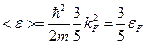
Таким образом, полная энергия электронного газа при :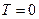

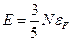
§30*. Уравнение состояния идеального электронного газа при 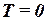. Критерий идеальности электронного газа

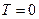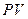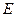Чтобы записать уравнение состояния электронного газа при , вспомним соотношение между и для идеального газа:

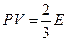
Теперь в качестве 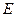подставим сюда :

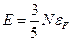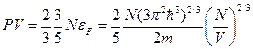
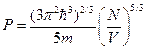(29)

Но ведь 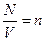и мы получили, что всё зависит от концентрации. Соотношение (29) называется уравнением состояния идеального газа при .

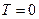Теперь рассмотрим критерий идеальности. Для больцмановского идеального газа писали критерий идеальности:

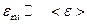
Для больцмановского газа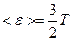

Для ферми газа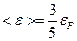

Мы оценивали энергию взаимодействия для электронного газа:

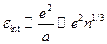
И видна принципиальная разница критериев идеальности для больцмановского газа и для ферми газа:

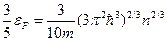
и видим такое различие:

для больцмановского газа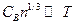

для ферми газа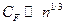

Т.е. для ферми газа условие идеальности противоположно условию идеальности для больцмановского газа. Но в условии для ферми газа нет температуры – это не удивительно, т.к. у нас ферми газ при .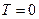

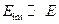
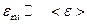
§31*. Числовые оценки параметров 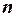, , 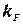, , 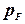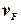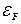и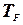

Начнём с концентрации. Рассчитаем концентрацию электронов в элементе ;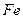

Здесь 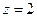.Посчитаем концентрацию электронов для такой среды:

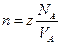
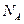- число Авогадро, а 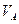- объём одного моля

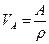
где 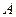- атомный вес, 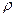- плотность железа.

Тогда

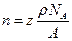
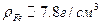
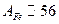
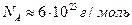
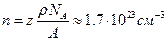
Рассчитаем :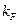

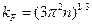
Тогда радиус сферы Ферми:

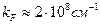
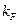- волновое число Ферми (так тоже называют).

Теперь оценим импульс Ферми.

,

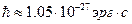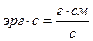
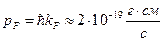
Оценим скорость Ферми.

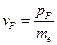
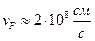- скорость фермиевских электронов.

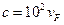- т.е. релятивистские эффекты можно не учитывать

Посчитаем энергию Ферми:

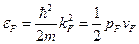
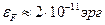
Часто температуру Ферми измеряют в энергетической шкале, а бывает удобнее в градусах:

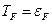- в энергетической шкале

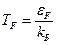- в градусах

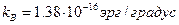- постоянная Больцмана

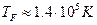
С температурой 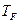связывают вырождение электронного газа. При комнатной температуре газ вырожденный.

Часто для описания вырожденного газа используют соотношения как для случая .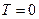

Экзаменационные вопросы по курсу “Статистическая физика”

1. Статистическое описание систем с большим числом степеней свободы

2. Метод статистической физики(элементы теории вероятностей)

3. Микро- и макро- параметры системы.

4. Свойство эргодичности системы.

5. Два способа усреднения в статистической физике

6. Понятие ансамбля систем

7. Эргодическая гипотеза

8. Равновесное состояние системы

9. Время релаксации

10. Квазизамкнутость и статистическая независимость подсистем

11. Принцип равновероятности микросостояний

12. Статистический вес макросостояния

13. Статистическая энтропия

14. Теорема Лиувилля

15. Микроканоническое распределение Гиббса

16. Каноническое распределение Гиббса

17. Принцип возрастания энтропии

18. Квазиклассическое приближение в статистической физике

19. Использование распределения Максвелла для расчёта средних: , , ,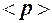

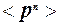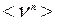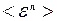
20. Большое каноническое распределение

21. Термодинамический потенциал Гиббса

22. Распределение Ферми-Дирака

23. Распределение Бозе-Эйнштейна

24. Ферми и Бозе газы элементарных частиц

25. Расчёт импульса Ферми для электронного газа при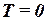

26. Расчёт энергии электронного газа при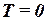

Экзаменационные задачи по курсу “Статистическая физика”

Задача 1. Математический маятник совершает гармонические колебания по закону

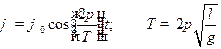Найти вероятность того, что при случайном измерении отклонения 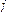маятника это значение будет лежать в интервале .

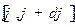Задача 2. Вероятность того, что 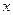и лежат в интервалах: 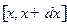и 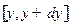дается выражением:

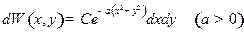
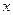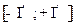Считая, что областями измерения переменных и является и 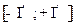, найти константу нормировки .

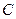Задача 3. Определить вероятность того, что значение величины 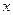будет лежать в интервале .

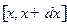Задача 4.Найти дисперсию энергии в случае канонического распределения Гиббса.

Задача 5. Найти дисперсию числа частиц в случае большого канонического распределения Гиббса.

Задача 6. Используя распределение Гиббса: 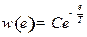получить различные формы распределения Максвелла:

1) вероятность того, что скорость любой частицы заданной системы лежит в интервалах , , ;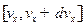

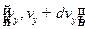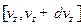2) вероятность того, что абсолютная величина скорости лежит в интервале ;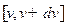

3) вероятность того, что кинетическая энергия любой частицы лежит в интервале ;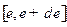

Задача 7.Используя распределение Максвелла, найти:

а) ;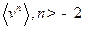

б) ;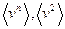

в) 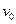(наиболее вероятное значение величины скорости);

Задача 8.Используя распределение Максвелла, найти дисперсию скорости 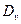и среднее квадратичное отклонение .

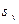Задача 9.Найти 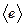и наиболее вероятное значение кинетической энергии частицы .

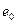Задача 10:Используя распределение Максвелла, найти дисперсию кинетической энергии 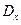, где .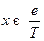

Задача 11.Найти вероятность того, что две частицы имеют абсолютную величину скорости относительного движения 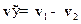в интервале 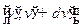. Найти .

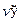Задача 12. Используя распределение Гиббса, найти для идеального газа, помещенного во внешнее потенциальное силовое поле 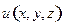, вероятность того, что координаты любой частицы будут лежать в интервалах , , .

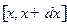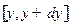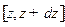Задача 13.Найти центр тяжести столба идеального газа в однородном поле тяжести, если ускорение поля тяжести 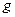, масса молекулы 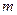, температура .

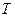Экзаменационные вопросы и задачи по курсу “Статистическая физика” (минимум)

1. Статистическое описание систем с большим числом степеней свободы.
2. Два способа усреднения в статистической физике.
3. Эргодическая гипотеза.
4. Теорема Лиувилля
5. Микроканоническое распределение Гиббса.
6. Каноническое распределение Гиббса
7. Квазиклассическое приближение в статистической физике.
8. Использование распределение Максвелла для расчета средних:
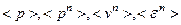
9. Распределение Ферми-Дирака.
10. Распределение Бозе-Эйнштейна.
11. Расчет импульса Ферми для электронного газа при Т=0.

Задачи:

Задача 1. Вероятность того, что 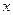и лежат в интервалах: 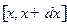и 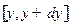дается выражением:

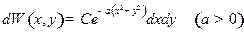
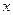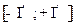Считая, что областями измерения переменных и является и 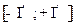, найти константу нормировки .

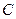Задача 2.Используя распределение Максвелла, найти:

а) ;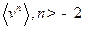

б) ;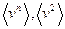

в) 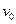(наиболее вероятное значение величины скорости);

Задача 3:Используя распределение Максвелла, найти дисперсию кинетической энергии 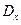, где .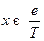

Задача 4.Найти центр тяжести столба идеального газа в однородном поле тяжести, если ускорение поля тяжести 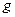, масса молекулы 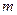, температура .

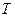Решение задач по курсу “Статистическая физика”

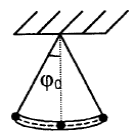
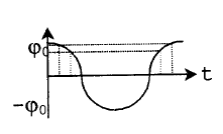
Задача 1. Математический маятник совершает гармонические колебания по закону

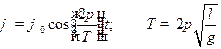Найти вероятность того, что при случайном измерении отклонения 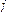маятника это значение будет лежать в интервале .

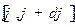Решение. Запишем закон колебания в ви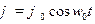де: , где 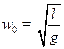. Тогда нам надо найти вероятность .

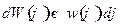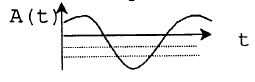
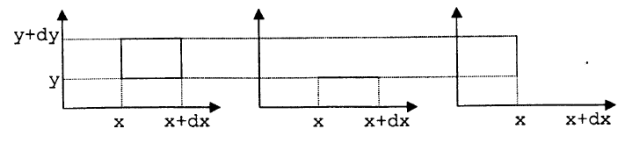
Из рисунка видно, что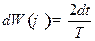

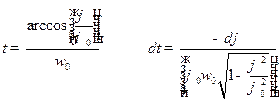
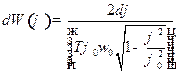
Обозначим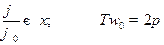

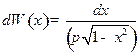
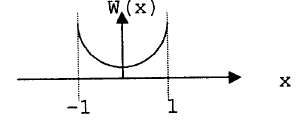
Как и ожидалось, площадь под кривой равна 1.

Ответ. 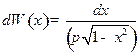, где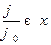

Дополнение.В общем случае график зависимости может не выражаться через линейные функции. Например:

Тогда необходимо подсчитать время, в течении которого параметр начодится в заданном интервале значений:

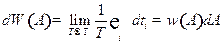
Гамма-функция Эйлера

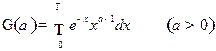
Свойства: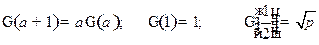

Задача 2. Вероятность того, что 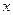и лежат в интервалах: и 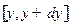дается выражением:

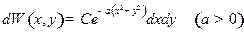
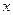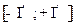Считая, что областями измерения переменных и является и 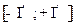, найти константу нормировки .

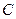Задача 3. Определить вероятность того, что значение величины 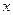будет лежать в интервале .

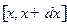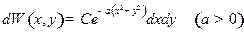
Решение.Условие нормировки: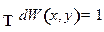

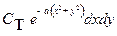=1

Переходим к полярным координатам: якобиан перехода:

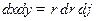
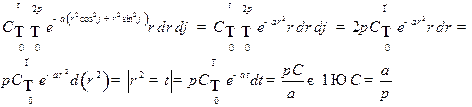
Первому рисунку отвечает функция распределения ;

второму - ; третьему -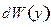

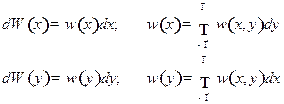
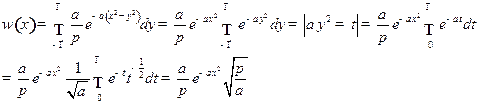
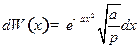
Аналогично: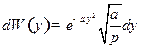

Ответ: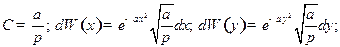

Задача 4.Найти дисперсию энергии в случае канонического распределения Гиббса.

Решение.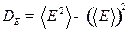

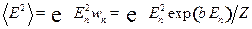
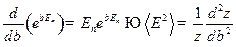
Аналогично: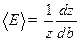

.

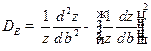Однако: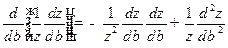

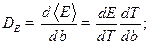
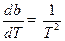
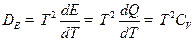(при )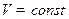

Ответ: 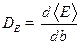;При .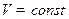

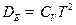Задача 5. Найти дисперсию числа частиц в случае большого канонического распределения Гиббса.

Решение.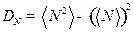

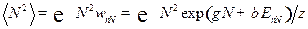
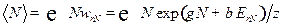
Видно, что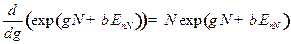

;

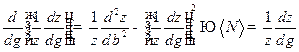
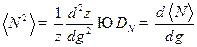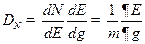
Ответ: ; .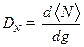

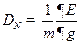Задача 6. Используя распределение Гиббса: 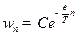получить различные формы распределения Максвелла:

1) вероятность того, что скорость любой частицы заданной системы лежит в интервалах , , ;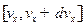

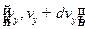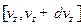2) вероятность того, что абсолютная величина скорости лежит в интервале ;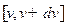

3) вероятность того, что кинетическая энергия любой частицы лежит в интервале ;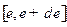

Решение:1) ,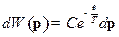

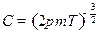
Так как 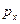, , 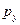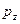статистически независимы, то:

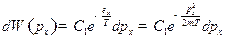
Из условия нормировки: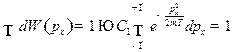

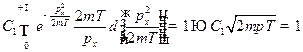
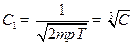
Аналогично: ;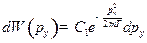

;

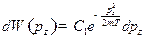Для нахождения 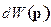перейдем к сферическим координатам:

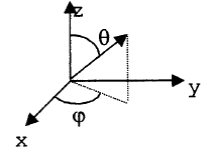
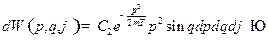
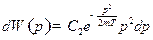
Найдем 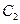из условия нормировки:

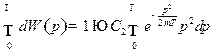
Сделаем замену переменных: 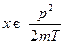. Тогда ;

,

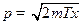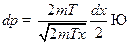
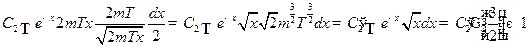где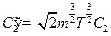

Таким образом,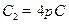

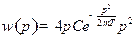
2)

,

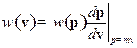
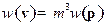
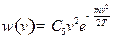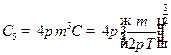
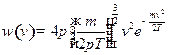
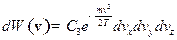
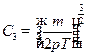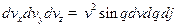
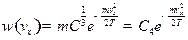, где

, где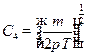

4)

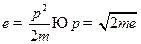
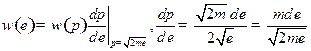
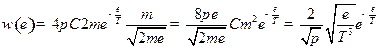
Ответ: 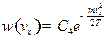,где

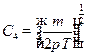
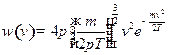
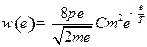, где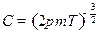

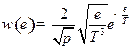
Задача 7.Используя распределение Максвелла, найти:

а) ;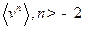

б) ;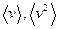

в) 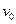(наиболее вероятное значение величины скорости);

Решение: ,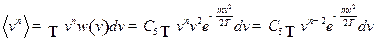

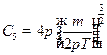
Сделаем замену переменных: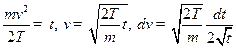

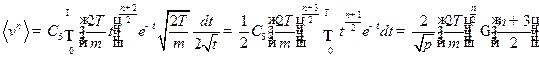
Если 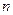- четное :

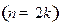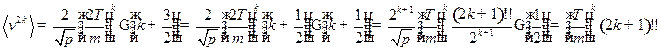
Если 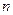-нечетное :

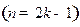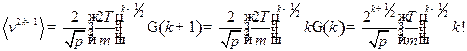
б) ,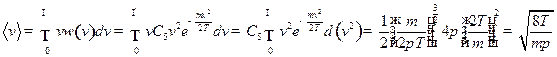

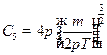
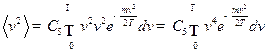
Сделаем замену переменных: ;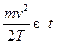

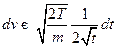
Тогда: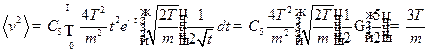

в) Ищем экстремум функции :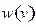

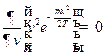
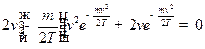
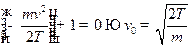
Ответ: Если 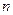-четное :

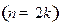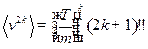
Если 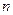-нечетное :

; ; ;

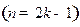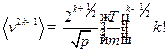
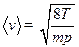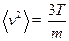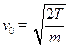Задача 8.Используя распределение Максвелла, найти дисперсию скорости 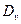и среднее квадратичное отклонение .

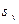Решение: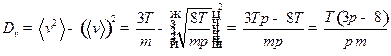

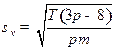
Задача 9.Найти 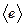и наиболее вероятное значение кинетической энергии частицы .

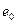Решение: Условимся решать задачу в СГС (к=1).

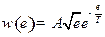, где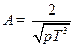

Обозначим: 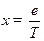. Тогда 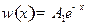, где