Комплексная диэлектрическая проницаемость
Свойства диэлектриков на переменном токе удобно рассматривать, пользуясь понятием комплексной диэлектрической проницаемости.
Как известно из курса общей физики, ток через реальный конденсатор опережает напряжение по фазе на угол, меньший, чем p/2. Такой конденсатор, помимо реактивной проводимости b, характеризуется и активной проводимостью g, которую удобно учесть, вводя комплексную диэлектрическую проницаемость
,
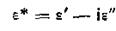где ε' и ε" — действительная и мнимая части комплексной диэлектрической проницаемости;
ε" также называют коэффициентом потерь.
Комплексная диэлектрическая проницаемость ε* определяет комплексную емкость C* конденсатора на переменном токе;
,
где С' == ε'Св,
С" = ε"Св, причем
Св — емкость соответствующего вакуумного конденсатора, т. е. конденсатора с теми же размерами, но без диэлектрика.
Полная комплексная проводимость конденсатора
,
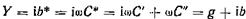где b == wС' — реактивная и
g = wC" — активная проводимости конденсатора.
Активный ток через конденсатор равняется
,
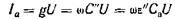и реактивный ток
.
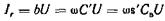Тангенс угла диэлектрических потерь tg d выражается через ε' и ε"; из и следует, что
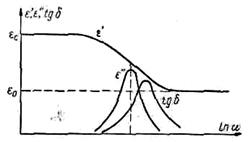 Рис. 7‑3. Частотные зависимости ε./, ε// и tg d диэлектрика с релаксационной поляризацией (без учета потерь сквозной проводимости) |
.
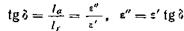Составляющие ε' и ε" комплексной диэлектрической проницаемости ε* зависят от температуры диэлектрика и частоты электрического поля. Частотные зависимости ε' и ε" диэлектрика с релаксационной поляризацией и сквозной проводимостью gv найдем, сопоставив выражения для активного тока и , и и для реактивного тока , и
,
.
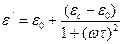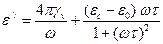Член 4pgv/w) связан со сквозной проводимостью. На достаточно высоких частотах этим членом можно пренебречь и выражение для
ε' диэлектрика с релаксационной поляризацией записать в следующем виде;
.
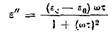Частотные зависимости ε./, ε// и tg dпоказаны на Рис. 7‑3. Как видно из рисунка и формул , и , диэлектрические проницаемости ε' и е* на низких частотах равняются статической диэлектрической проницаемости εc. С повышением частоты величина ε' уменьшается и стремится к оптической диэлектрической проницаемости ε0.
В частотном ходе ε" имеется максимум, который лежит при несколько меньших частотах, чем максимум tg d.
Релаксационные потери при одном времени релаксации
Теория релаксационных потерь объясняет природу релаксационных диэлектрических потерь с молекулярной точки зрения и рассматривает частотные и температурные зависимости комплексной диэлектрической проницаемости ε* и tg d диэлектриков с релаксационной поляризацией.