Задачи для самостоятельного решения и контрольных заданий

1. Найти среднюю длину свободного пробега и среднее время между столкновениями молекул азота, находящегося: а) при нормальных условиях; б) при температуре t = 0° С и давлении p = 1 нПа (такое давление позволяет получать современные вакуумные насосы). [а) 0,06 мкм, 0,13 нс; б) 6 нм, 3,8 ч]

2. Баллон вместимостью V=10 л содержит водород массой m=1 г. Определить среднюю длину свободного пробега молекул.[1,55 нм]

3. Определить плотность 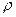разреженного водорода, если средняя длина свободного пробега 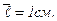[1,55 кг/м³]

4. Найти зависимость среднего числа столкновений 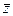молекулы идеального газа в 1 с от давления при следующих процессах: 1) изохорном; 2) изотермическом. Изобразить эти зависимости на графиках.[1) 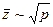; 2) ]

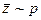5. Азот находится при нормальных условиях. Найти: а) число столкновений, испытываемых в среднем каждой молекулой за одну секунду; б) число всех столкновений, происходящих между молекулами в 1 см³ азота ежесекундно. [а) 0,74×10¹⁰с^-1; б) 1×10²⁹с^-1см^-3]

6. Оценить среднюю длину свободного пробега 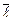и коэффициент диффузии D ионов в водородной плазме. Температура плазмы 10⁷К, число ионов в 1 см³ плазмы равно 10¹⁵. При указанной температуре эффективное сечение иона водорода считать равным 4×10^-20см². [ l ~ 10²м, D ~ 10⁷ м²/c]

7. Найти, как зависят от давления средняя длина свободного пробега и число столкновений в 1 с молекул идеального газа, если газ совершает процесс: а) изохорический, б) изотермический, в) адиабатический. Эффективный диаметр молекул считать постоянным. а) 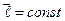, 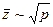; б) , .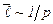

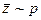8. Найти, как зависят от температуры средняя длина свободного пробега и число столкновений в 1 с молекул идеального газа, если масса газа постоянна и газ совершает процесс: а) изохорический, б) изобарический, в) адиабатический.

[а) 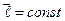, 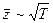; б) , ]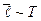

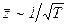9. Зная коэффициент вязкости гелия при нормальных условиях (h = 18,9 мкПа×с), вычислить эффективный диаметр его атома. [d = 0,18 нм]

10. Коэффициент теплопроводности гелия в 8,7 раза больше, чем у аргона (при нормальных условиях). Найти отношение эффективных диаметров атомов аргона и гелия. [1,7]

11. Коэффициент диффузии кислорода (О₂) при температуре 0°С равен 0,19 см²/с. Определить среднюю длину свободного пробега молекул газа. [1,35×10^-7 м]

12. Давление двухатомного газа вследствие сжатия увеличивается в 10 раз. Определить, как изменится длина свободного пробега молекул в газе и коэффициент вязкости газа. Рассмотреть случай, когда сжатие происходит: а) изотермически, б) адиабатически. [а) 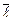уменьшится в 10 раз; h останется неизменным, б) 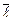уменьшится в 5,2 раза, h увеличится в 1,39 раза]

13. Двухатомный газ адиабатически расширяется до объема, в два раза большего начального. Определить, как изменится коэффициент теплопроводности и коэффициент диффузии газа. [ 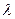уменьшится в 1,15 раза; D увеличится в 1,75 раза]

14. Между двумя параллельными плоскими очень большими пластинами имеется зазор а = 1 см. Между пластинами поддерживается разность температур DТ = 1 К (Т₁ = 299,5 К, Т₂ = 300,5 К). Зазор заполнен аргоном при давлении 1,0×10⁵ Па. Оценить плотность потока тепла. [0,5 Вт/м²]

15. Найти распределение температуры в пространстве между двумя коаксиальными цилиндрами с радиусами R₁ и R₂, заполненном однородным теплопроводящим веществом, если температуры цилиндров постоянны и равны соответственно Т₁ и Т₂. [ ]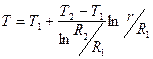

16. Одноатомный идеальный газ заполняет пространство между двумя очень длинными коаксиальными цилиндрами с радиусами R₁ и R₂ (R₂ > R₁). Внутренний цилиндр поддерживается при температуре Т₁, внешний при температуре Т₂ (Т₁ > Т₂). Найти поток тепла, приходящийся на единицу длины цилиндров. Считать, что длина свободного пробега молекул газа много меньше расстояния между цилиндрами. [ ]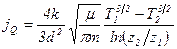

17. Через площадку S = 100 см² за время t = 10 с вследствие диффузии проходит некоторое количество азота. Градиент плотности в направлении, перпендикулярном площадке равен 1,26 кг/м⁴. Процесс идет при температуре 300 К, средняя длина свободного пробега молекул азота 10^-7м, эффективный диаметр его молекул 3,75×10^-10м. Определить количество продиффундировавшего азота за указанное время через площадку S.

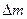[ =2,1×10^-6кг]

18. Пространство между двумя большими параллельными пластинами заполнено средой, коэффициент теплопроводности которой изменяется с температурой по закону 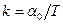, где a₀ – постоянная для данной среды величина. Температуры пластин Т₁ и Т₂ поддерживаются постоянными (Т₁ > Т₂). Расстояние между пластинами L. Найти плотность потока тепла и температуру Т в среде как функцию x, где x– расстояние отсчитанное от пластины, температура которой Т₁.

[ ; ]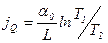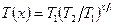