Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
Молекулярная физика. Термодинамика.
1.Статистический и термодинамический методы
2.Молекулярно-кинетическая теория идеальных газов
2.1.Основные определения
2.2.Опытные законы идеального газа
2.3.Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева
2.4.Основное уравнение молекулярно-кинетической теории идеального газа
2.5.Распределение Максвелла
2.6.Распределение Больцмана
3.Термодинамика
3.1.Внутренняя энергия. Закон равномерного распределения энергии по степеням свободы
3.2.Первое начало термодинамики
3.3.Работа газа при изменении его объема
3.4.Теплоемкость
3.5.Первое начало термодинамики и изопроцессы
3.5.1.Изохорный процесс (V = const)
3.5.2.Изобарный процесс (p = const)
3.5.3.Изотермический процесс (T = const)
3.5.4. Адиабатический процесс (dQ = 0)
3.5.5. Политропные процессы
3.6.Круговой процесс (цикл). Обратимые и необратимые процессы. Цикл Карно.
3.7.Второе начало термодинамики
3.8.Реальные газы
3.8.1.Силы межмолекулярного взаимодействия
3.8.2.Уравнение Ван-дер-Ваальса
3.8.3.Внутренняя энергия реального газа
3.8.4.Эффект Джоуля-Томсона. Сжижение газов.
Статистический и термодинамический методы
Молекулярная физика и термодинамика - разделы физики, в которых изучаются макроскопические процессы, связанные с огромным числом содержащихся в телах атомов и молекул. Для изучения этих процессов применяют два принципиально различающихся (но взаимно дополняющих друг друга) метода: статистический (молекулярно-кинетический) итермодинамический.
Молекулярная физика - раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул изучаются с помощью статистического метода, который основан на том, что свойства макроскопической системы определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т.д.). Например, температура тела определяется средней скоростью хаотического движения его молекул и нельзя говорить о температуре одной молекулы.
Термодинамика - раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы , которые лежат в основе этих превращений, а основывается на двух началах термодинамики - фундаментальных законах, установленных экспериментальным путем.
Статистические методы физики не могут быть использованы во многих разделах физики и химии, тогда как термодинамические методы универсальны. Однако статистические методы позволяют устанавливать микроскопическое строение вещества, тогда как термодинамические методы лишь устанавливают связи между макроскопическими свойствами. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь методами исследования.
Молекулярно-кинетическая теория идеальных газов
Основные определения
Объектом исследования в молекулярно-кинетической теории является газ. Считается, что молекулы газа, совершая беспорядоченые движения, не связаны силами взаимодействия и поэтому они движутся свободно, стремясь, в результате соударений, разлететься во все стороны, заполняя весь предоставленный им объем. Таким образом, газ принимает объем того сосуда, который газ занимает.
Идеальный газ- это газ, для которого: собственный объем его молекул пренебрежимо мал по сравнению с объемом сосуда; между молекулами газа отсутствуют силы взаимодействия; столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Для многих реальных газов модель идеального газа хорошо описывает их макро свойства.
Термодинамическая система - совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой).
Состояние системы - совокупность физических величин (термодинамических параметров, параметров состояния), которые характеризуют свойства термодинамической системы: температура, давление, удельный объем.
Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В системе СИ разрешено использование термодинамическойи практической шкалы температур. В термодинамической шкале тройная точка воды (температура, при которой лед, вода и пар при давлении 609 Па находятся в термодинамическом равновесии) считается равной Т = 273.16 градуса Кельвина [K]. В практической шкале температуры замерзания и кипения воды при давлении 101300 Па считаются равными, соответственно, t = 0 и t =100 градусов Цельсия [C]. Эти температуры связаны между собой соотношением
T = 273.15 + t.
Температура Т = 0 К называется нулем Кельвин, согласно современным представлениям эта температура недостижима, хотя приближение к ней сколь угодно близко возможно.
Давление - физическая величина, определяемая нормальной силой F, действующей со стороны газа (жидкости) на единичную площадку, помещенную внутрь газа (жидкости) p = F/S, где S - размер площадки. Единица давления - паскаль [Па]: 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2 (1 Па = 1 Н/м2).
Удельный объем - это объем единицы массы v = V/m = 1/r, где V - объем массы m, r - плотность однородного тела. Поскольку для однородного тела v ~ V, то макроскопические свойства однородного тела можно характеризовать как v, так и V.
Термодинамический процесс- любое изменение в термодинамической системе, приводящее к изменению хотя бы одного из ее термодинамических параметров. Термодинамическое равновесие - такое состояние макроскопической системы, когда ее термодинамические параметры не изменяются с течением времени. Равновесные процессы - процессы, которые протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало.
Изопроцессы- это равновесные процессы, при которых один из основных параметров состояния сохраняется постоянным. Изобарный процесс- процесс, протекающий при постоянном давлении (в координатах V,t он изображается изобарой). Изохорный процесс - процесс, протекающий при постоянном объеме (в координатах p,t он изображается изохорой). Изотермический процесс- процесс, протекающий при постоянной температуре (в координатах p,V он изображается изотермой). Адиабатический процесс - это процесс, при котором отсутствует теплообмен между системой и окружающей средой (в координатах p,V он изображается адиабатой).
Постоянная (число) Авогадро - число молекул в одном моле NA=6.022.1023.
Нормальные условия: p = 101300 Па, Т = 273.16 К.
2.2.Опытные законы идеального газа
Закон Бойля-Мариотта: при T=const, m=const pV = const (изотермический процесс , рис.1).
Закон Гей-Люссака: при p=const, m=constV=VoaT (изобарный процесс , рис.2), при V=const, m=constp=poaT (изохорный процесс , рис.3).
Закон Авогадро: моль любого газа при одинаковой температуре и давлении занимает одинаковый объем Vm (при нормальных условиях Vm = 22.41.10-3 м3).
Закон Дальтона: давление смеси газов равно сумме парциальных давлений р1, р2,... рn входящих в нее газов p = p1+p2+...+pn. Парциальное давление-давление, которое производил бы газ, входящий в состав газовой смеси, если бы он занимал объем, равный объему смеси при той же температуре.
p V p
 |  | ||
T2 p2 V2
T1<T2 p1>p2 V1>V2
T1 p1 V1
V T T
Рис.1. Рис.2. Рис.3.
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
Функциональная связь между давлением, объемом и температурой называется уравнением состояния. Для идеального газа, используя законы Бойля-Мариотта, Гей-Люссака и Авогадро, можно получить:
уравнение Клапейрона-Менделеева для одного моля газаpVm = RT, (1a)
где R = 8.31 Дж/моль.К - газовая постоянная (она находится после подстановки в последнее уравнение нормальных условий)
уравнение Клапейрона-Менделеева для произвольной массы газаpV =(m/M)RT = nRT, (1b)
где М - масса одного моля (молярная масса), n = m/M - количество вещества.
Можно ввести постоянную Больцмана k = R/NA = 1.38.10-23 Дж/К и тогда уравнение Клапейрона-Менделеева имеет вид p = nkT, (1c)
где n = NA/Vm - число молекул в единице объема (концентрация молекул), т.е. при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул (в 1 м3 при нормальных условиях содержится NL = 2.68.1025 молекул - число Лошмидта).
2.4.Основное уравнение молекулярно-кинетической теории идеальных газоввыводится в предположении, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие.
p = (1/3)nm<vкв>2, (2)
где n = N/V - концентрация молекул газа, N - число молекул газа, V - объем газа, <vкв> = [(1/N)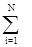 
vi2]1/2 - среднеквадратичная скорость молекул, vi - скорость i-молекулы, m - масса одной молекулы.
Суммарная кинетическая энергия поступательного движения всех молекул газа E = N[m<vкв>2/2] и, следовательно, уравнение (2) можно записать pV = (2/3)E.
Если сравнить уравнение (2) с уравнением Клапейрона-Менделеева (1), то можно получить выражения для среднеквадратичной скорости молекул <vкв> =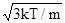 
(3a)
и для средней кинетической энергии поступательного движения одной молекулы идеального газа
<Ek> = 3kT/2.
(4)
Таким образом, термодинамическая температура Т является мерой средней кинетической энергии поступательного движения молекул идеального газа и формула (4) раскрывает молекулярно-кинетическое толкование температуры.