Вязкость. вязкая жидкость. Стационарное течение вязкой жидкости. Коэффициент жидкостей. Нормальная и аномальная вязкости

Физический смысл коэффициента вязкости можно выяснить из следующих соображений. При установившемся потоке жидкости в трубе различные слои движущейся жидкости имеют различные скорости. Наибольшую скорость имеет слой, текущий по центральной части трубы. Слой, непосредственно прилегающий к стенкам трубы, благодаря прилипанию частичек жидкости к стенкам трубы, имеет скорость 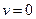. Поэтому распределение скорости текущей жидкости по трубе определяется величиной 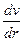(градиент скорости), которая показывает изменение скорости на единицу длины радиуса трубы. Согласно закону Ньютона, сила внутреннего трения между слоями определяется формулой:

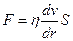
где η – коэффициент вязкости;

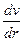- градиент скорости;

S – площадь поверхности, к которой приложена сила.

Из этой формулы следует:

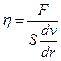
Если предположить, что S равняется единице поверхности и градиент скорости равен единице, то η = F, то есть коэффициент вязкости численно равен силе внутреннего трения между слоями, действующей на единицу поверхности при градиенте скорости равном единице.

В системе СИ коэффициент вязкости измеряется в Ньютон секундах на квадратный метр и имеет размерность

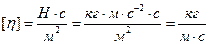
Стационарное течение жидкости - это такое течение, при котором скорость жидкости в каждой данной точке остается постоянной как по величине, так и по направлению. Для стационарного течения форма и расположение линий тока со временем не изменяются.

В случае стационарного течения скорость жидкости в любой точке объе­ма остается неизменной. Линии тока при стационарном течении остаются неизменными и совпадают с траекто­рией отдельных частиц жидкости.

Часть жидкости, ограниченную линиями тока, называют трубкой тока.

Формула Пуазейля : При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости. где p1 − p2 = Δp — перепад давления на концах капилляра, Па; Q — секундный объёмный расход жидкости, м³/с; R — радиус капилляра, м; d — диаметр капилляра, м; η — коэффициент динамической вязкости, Па·с; l — длина трубы, м.

Для аномально вязких систем характер изменения вязкости при разных напряжениях различается (рис. 6.2). При малых напряжениях зависимости т)=/(Р) отвечают закону Ньютона, характерному для нормальных низкомолекулярных жидкостей. В отличие от последних коэффициент т1о (называемый наибольшей ньютоновской вязкостью) для полимеров и дисперсных систем в этой области напряжений весьма высок (10 —10 Па-с). С увеличением напряжения сдвига происходит разрушение малопрочной пространственной структуры (сетки) системы и скорость течения аномально возрастает, пока при относительно больших напряжениях структура не будет разрушена полностью и в процессе течения не будет успевать восстанавливаться. Поэтому при больших напряжениях система характеризуется также ньютоновским законом течения, но коэффициент т)т (называемый наименьшей ньютоновской вязкостью) намного меньше, чем т о.

Для нормальных ньютоновских жидкостей, представляющих индивидуальные вещества либо молекулярно-дисперсные смеси или растворы, внутреннее трение (вязкость) при данных температуре и давлении является постоянным физическим свойством. Вязкость не зависит от условий определения и скорости перемещения частиц (течения), если не создается условий для турбулентного движения. Ньютоновскими или нормально вязкими называют жидкости, вязкость которых не зависит ни от приложенного давления, ни от градиента скорости

Гомогенные и гетерогенные системы , компоненты системы..гетерогенное равновесие фаз.диаграмма фазового равновесия(диаграмма состояния вещества ) T-X диаграммы состояния двойных сисетм. Количественное соотношение фаз и правило рычага.

Гомогенной называют такую систему, химический состав и физические свойства которой во всех ее частях одинаковы или изменяются непрерывно (без скачка) от одной точки системы к другой, а также между любыми частями которой нет поверхности раздела. Примером гомогенной системы может служить смесь газов, жидкий и твердый раствор, а также любое химически однородное тело.