Дифференциальное уравнение затухающих колебаний

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. В наиболее часто встречающемся случае сила сопротивления F пропорциональна величине скорости.

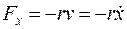. (20.1)

гдеr - коэффициент сопротивления среды. Знак минус обусловлен тем, что сила трения и скорость имеют противоположные направления.

При наличии сил сопротивления второй закон Ньютона, имеет вид:

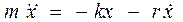. (20.2)

Применив обозначения: 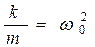, и 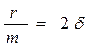получим дифференциальное уравнение затухающих колебаний:

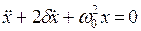, (20.3)

где δ –коэффициент затухания, он определяет, как быстро амплитуда колебаний уменьшается до нуля, ω₀– собственная частота колебаний – частота, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды.

Свободные затухающие колебания – колебания, амплитуда которых уменьшается с течением времени из-за потерь энергии реальной колебательной системы.

Решением уравнения (20.3) является выражение

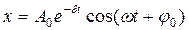, (20.4)

ω–циклическая частота затухающих колебаний, которая связана с собственной частотой соотношением

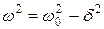. (20.5)

При подстановке значения коэффициента затухания в формулу (20.5) получим

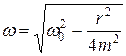. (20.6)

Из уравнения (20.3) видно, что амплитуда А изменяется по экспоненциальному закону:

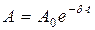, (20.7)

где А₀- начальная амплитуда,А - амплитуда затухающих колебаний.

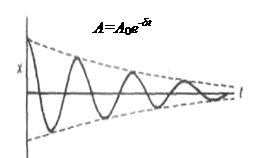
Зависимость (20.4).показана на рис.20.1 сплошной линией. А пунктирными линиями показаны пределы, в которых находятся смещения колебаний точки х. или функция изменения амплитуды описанная уравнением (20.7).

Промежуток времени t= 1/d- в течение, которого амплитуда затухающих колебаний уменьшается в ераз, называется – временем релаксации.

Рис.20.1

Затухающие колебания не являются периодическими, и строго говоря, к ним не применимо понятие периода или частоты. Однако, при малых затуханиях можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами колеблющейся физической величины, тогда период затухающих колебаний с учетом формулы (20.6) определяется как:

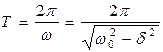. (20.8)

Если амплитуды двух последовательных колебаний A(t) и A(t+T) отличаются на период, то их отношение называется декрементом затухания.

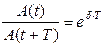(20.9)

логарифм данного выражения называется – логарифмическим декрементом затухания θ

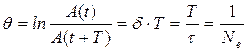, (20.10)

N_e--число колебаний, совершаемых за время уменьшения амплитуды в е раз.

Для данной колебательной системы логарифмический декремент затухания величина постоянная.

Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна:

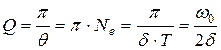. (20.11)

Из формулы (20.12) следует, что добротность пропорциональна числу колебаний N_e совершаемых системой за время релаксации.

Например, добротность пружинного маятника

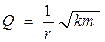. (20.12)

При увеличении коэффициента затухания период затухающих колебаний растет и при δ = ω₀ превращается в бесконечность, т.е. движение перестает быть периодическим. Колеблющаяся величина стремится к нулю, процесс не будет колебательным. Такой процесс называется апериодическим.

При условии 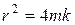(т.е. выполняется соотношение ω₀ ~ δ) колебательная система приходит в состояние равновесия за самое короткое время. Такое явление называется демпфированием. Примерами систем, в которых демпфирование оказывается полезным, являются устройства для закрывания дверей и амортизаторы автомобилей. Обычно их конструируют таким образом, чтобы затухание было критическим (демпфированным). Однако по мере износа этих устройств демпфирование ослабляется, двери начинают хлопать, автомобиль раскачивается, наезжая на неровности дороги. Явление демпфирования применяется при проектировке инерциальных ремней безопасности – в автомобилях. Эта идея также может быть внедрена в виде поясов безопасности для выполнения наружных высотных, ремонтных и строительных работ (т.к. в настоящее время возникает потребность внедрения новой строительной специальности – городской альпинизм).

За последнее десятилетие произошел сдвиг в отношении проектировщиков к учету взаимодействия сооружений с грунтовыми основаниями. Практически во всех проектах в той или иной форме принимается во внимание податливость основания.

Наиболее распространенный подход к моделированию взаимодействия сооружений с грунтом - “платформенная модель”. Суть его состоит в том, что сейсмическое воздействие подается на жесткую платформу, на которой с помощью определенного подвеса закреплена модель сооружения. Обычно этот подвес включает в себя распределенные пружины и демпферы. Преимущество “платформенной модели”- возможность проведения ее расчета с помощью тех же программ, что и расчета сооружения на жестком основании.

Для сооружений на жестких фундаментах поверхностного заложения и для вертикально распространяющихся сейсмических волн в горизонтально-слоистой среде такая модель является точной при том дополнительном условии, что жесткостные и демпфирующие свойства (способность к затуханию вынужденных колебаний) подвеса точно моделируют динамические характеристики штампа на грунтовом основании. Считается, что для основания в виде однородного полупространства динамические характеристики (жесткости) с достаточной точностью могут быть представлены пружинами, а демпфирующие - вязкими демпферами.

В общем случае свойства пружин и демпферов, моделирующих динамические жесткости основания в виде жесткого штампа с линейными свойствами как функции частоты. Однако пока в большинстве расчетов за основу берется статическая жесткость штампа (иногда она определяется достаточно изощренными методами), а демпфирование учитывается либо заданием модальных коэффициентов на уровне примерно 5 %, либо постановкой так называемых “акустических” не отражающих границ (распределенных демпферов).

Существует много способов искусственного введения трения в систему. Это может быть осуществлено, например, электрическим способом, однако возможны и чисто механические методы демпфирования. Вот некоторые из них:

1. Вязкое трение в жидкости. Простым примером является гидравлический демпфер, который состоит из поршня, перемещающегося в цилиндре; трение возникает при перетекании жидкости (часто вместо жидкости используется воздух) в тонком зазоре между поршнем и стенкой цилиндра. В некоторых других устройствах используются лопасти, движущиеся в масле или силиконовой жидкости.

2. Материалы с высоким уровнем рассеяния энергии. При ударе по "колоколу", изготовленному из специального сплава меди и марганца, вместо звона слышится глухой стук. В амортизирующих опорах часто используют резину; это отчасти связано с ее высокими демпфирующими характеристиками. Лопатки компрессоров газовых турбин иногда изготавливают из волокнистых полимерных материалов, обладающих значительным внутренним трением.

3. Демпфирующие покрытия панелей. Существуют такие вещества, что если нанести их на поверхность металлической панели, то при ударе по панели вместо характерного для металлов звука слышен глухой стук.

4. Сухое трение, возникающее при взаимном скольжении поверхностей в процессе вибрации. Этот способ используется, например, в некоторых компрессорах газовых турбин, где осуществлено шарнирное крепление лопаток к ротору. Кроме того, в некоторые пружины с целью демпфирования вставляются пучки металлической проволока.

5. Слоистые конструкции. Панели, состоящие из тонких металлических листов, разделенных тонким слоем вязкоупругого материала, обладают хорошими звукоизолирующими свойствами.

6. Пенопластовые или резиновые прокладки. Яйцо или электрическую лампочку, тщательно упакованные в подходящий материал, можно без всякого риска бросать с большой высоты на твердый пол.

Вынужденные колебания

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы с циклической частотой ω

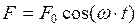. (20.13)

В данном случае с учетом силы (20.13) уравнение движения (20.2) будет иметь вид:

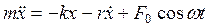. (20.14)

После деления на m и преобразования (20.3) получим неоднородное дифференциальное уравнение второго порядка:

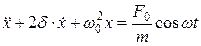, (20.15)

где ω – частоты вынуждающей силы.

Решение такого неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Общее решение записывается в виде:

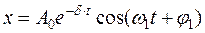, (20.16)

где .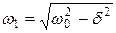

Частное решение имеет вид:

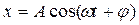, (20.17)

где А- амплитуда вынужденных колебаний.

Для определения амплитуды вынужденных колебаний А и сдвига фазы φ в уравнение (20.15) подставим значения первой и второй производной уравнения (20.17). Для начала продифференцируем:

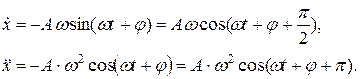(20.18)

Подставляя (20.18) в (20.16) и после некоторых математических преобразований, и применяя метод векторных диаграмм, получим значение амплитуды вынужденного колебания А и сдвига фазы φ:

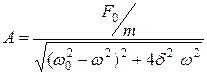, (20.19)

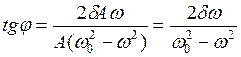. (20.20)

Из уравнения (20.19) видно, что амплитуда вынужденных колебания зависит от амплитуды вынуждающей силы. Подставим значения А и φ из уравнений (20.19) и (20.20) в уравнение (20.17) и запишем частное решение неоднородного уравнения для вынужденных электромагнитных колебаний:

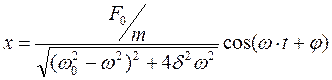. (20.21)

График вынужденных колебаний представлен на рис.20.2. Решение неоднородного дифференциального уравнения второго порядка (20.15) состоит из двух слагаемых. Слагаемое общего решения (20.16) играет заметную роль только в начальной стадии процесса при установлении колебаний. В дальнейшем этим слагаемым можно пренебречь т.к. оно содержит член е^-dt . Т.о. вынужденные колебания описываются функцией гармонических колебаний (20.21) с частотой равной частоте ω вынуждающей силы F. Для данной колебательной системы с известной частотой и коэффициентом затухания амплитуда вынужденных колебаний (20.19) зависит от амплитуды и частоты вынуждающей силы.

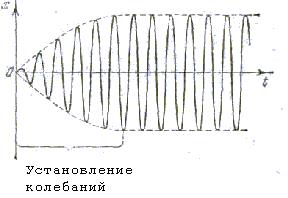Рис.20.2.

Одним из видов вынужденных колебаний являются вибрации, которые сопровождают нас повсюду и в большинстве случаев эти вибрации являются нежелательными. В первую очередь можно назвать вибрации и колебания авто и железнодорожного транспорта, моторов и станков, нефтяных и газовых платформ, зданий и сооружений в зоне повышенной сейсмической опасности. Во всех случаях стоит задача изоляции от источника вибраций. Несмотря на все конструкционные различия суть системы вибраций одинакова. Пассивная система состоит из пружины и демпфера. Пружина призвана смягчить вибрации и толчки, а демпфер погасить возникшие в системе колебания. Активная система использует также дополнительную пару, состоящую из акселерометра и электромагнитного привода, что позволяет достигнуть исключительную высокую степень виброизоляции.