Закон всемирного тяготения
Закон всемирного тяготения Ньютона многие не принимали как не соответствующий здравому смыслу, как теорию действия на расстоянии. X. Гюйгенс развивал теорию близкодействия, гидродинамическую модель вращающейся жидкости, подобную вихрям Декарта. Этой модели придерживался и Г.Лейбниц как более наглядной в объяснении воздействия тел. Страстным пропаганди-
стом теории тяготения Ньютона стал Вольтер. Его популярная книга «Элементы учения Ньютона» (1738) сыграла большую роль в изменении общественного и научного мировоззрения во Франции. Критерием проверки закона тяготения на Земле, и стала форма Земли. По вихревой модели наша планета должна была быть вытянута у полюсов, а по теории Ньютона — сплюснута.
Для уточнения формы Земли были организованы экспедиции в Перу и Лапландию (1735, 1736—1737). П. Мопертюи, руководивший экспедицией на север, показал сплюснутость Земли у полюсов. В этой экспедиции принимал участие А. Клеро. После обработки полученных результатов он опубликовал книгу «Теория фигуры Земли», построенную на основе гидростатической модели эллипсоида вращения. Клеро предположил, что Земля ранее была жидкой, ее частицы взаимодействовали друг с другом по закону всемирного тяготения, и вся масса медленно вращалась вокруг оси. Эта работа имела огромное значение для геодезии и теории Земли.
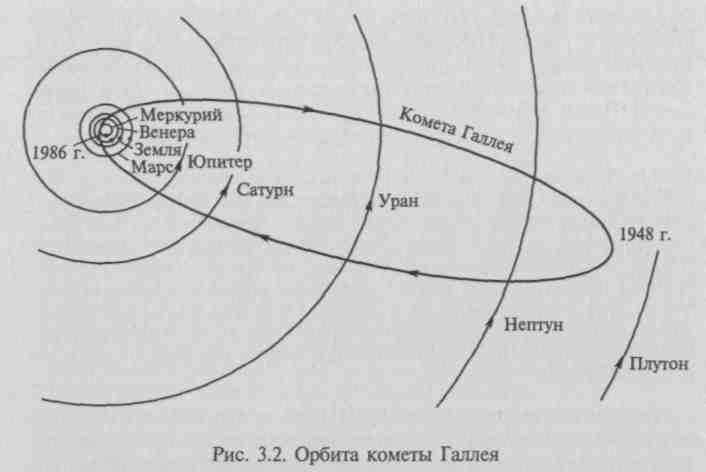
Тем самым теория тяготения Ньютона получила подтверждение на Земле. Это нанесло удар по взглядам ученых, которые считали, что все процессы физического мира должны представляться наглядно. Солнечная система у Ньютона — гигантский механизм, в котором гравитация управляет движением всех его элементов. Но, изучая движение конкретной планеты, нельзя не учитывать воздействие других планет и их спутников, хотя оно и мало по сравнению с притяжением Солнца. Его называют возмущением, или пертурбацией (от лат. perturbatio — расстройство, смятение). Английский астроном и геофизик Э. Галлей, изучая материалы наблюдений, обратил внимание на сходство орбит комет в 1456, 1531, 1607, 1682 гг. и периодичность их появления (около 76 лет). Он заключил, что это была одна и та же комета, и предсказал ее возвращение в 1758 г. (рис. 3.2). Но из-за возмущающего действия Юпитера и Сатурна комета Галлея появилась только в следующем году почти в точном соответствии с расчетами Клеро (он ошибся только на 19 дней!). Предсказание возвращения кометы стало первой убедительной победой теории Ньютона. Клеро проверил теорию Ньютона и по движениям Луны. Он составил точные лунные таблицы и по своим разработкам написал книгу «Теория движения Луны» (1751).
Близость Луны к Земле (около 400 тыс. км) позволяла провести измерения достаточно точно. Еще в 1693 г. Галлей заметил, что современные ему данные по орбите Луны расходятся с древними наблюдениями так, будто радиус орбиты уменьшается за столетие на 10". Эйлер связал ускорение с торможением в окружающей среде, а не с тяготением, Лаплас — с малыми изменениями вытянутости земной орбиты из-за планетных возмущений. Их объяснения (1787) верны только отчасти: такие колебания существуют, вызывая наступления ледников, так как за десятки тысяч лет
широта местности может измениться. Но, кроме этого, есть еще ускорение Луны, вызванное приливами. Этот эффект кажущийся, а причина — замедление вращения Земли из-за приливного трения. Оценка эффекта дает за 1 млрд лет удвоение суток и удаление Луны от Земли на расстояние до 600 тыс. км.
Другое явление, позволявшее усомниться в пригодности закона Ньютона, было ранее замеченное некоторое ускорение движения Юпитера и замедление движения Сатурна (Кеплер, 1625; Гал-лей, 1695). Оно должно бы за долгие миллионы лет разрушить Солнечную систему, но этого не произошло. Анализ планетных возмущений привел Лагранжа (1776) и Лапласа (1784) к теореме устойчивости Солнечной системы: взаимные возмущения планет, движущихся по почти круговым орбитам примерно в одной плоскости и в одну сторону, приводят лишь к почти периодическим колебаниям эксцентриситетов и наклонений вблизи нуля, тогда как расстояния до Солнца колеблются вблизи своих начальных значений. Или — большие оси кеплеровских эллипсов не испытывают вековых возмущений. Эта теорема доказана Лапласом для первых членов ряда возмущений. Взаимные возмущения Юпитера и Сатурна существуют, и их значения колеблются с периодом в 900 лет. За 450 лет накопления возмущений эта величина составляет меньше одного градуса.
Самым убедительным подтверждением ньютонова закона тяготения в Солнечной системе явилось открытие «на кончике пера» еще одной планеты, названной Нептуном. Открытие этой плане-
ты — триумф науки и, конечно, закона всемирного тяготения. Границы Солнечной системы расширились почти вдвое.
В 1781 г. У. Гершель открыл новую планету Уран. Для нее были вычислены элементы орбиты и составлены таблицы движения. Но заметили, что Уран в своем движении отклоняется от рассчитанного по закону Ньютона: за три года — на 2' при погрешности измерений в доли секунд. Французский астроном У. Леверье предположил, что это отклонение вызвано влиянием неизвестной планеты, находящейся дальше Урана, и сделал расчет ее орбиты. Леверье сообщил результаты в письме от 18 сентября 1846 г. берлинскому астроному Галле, который имел звездные карты, содержавшие слабые звезды. Галле обнаружил в указанном месте слабую звездочку 8-й величины, которой на картах не было. Через день она переместилась относительно ближайших звезд, а в более сильный телескоп удалось разглядеть маленький диск. Это была предвычисленная по закону всемирного тяготения новая планета Солнечной системы. Ее положение на небе отличалось от предсказанного расчетом Леверье всего на 52". В это же время английский студент Дж.Адамс, впоследствии известный астроном, независимо от Леверье проделал нужные расчеты, поэтому у этого предсказания два автора, хотя официально признан первый. Позже было обнаружено, что в зарисовках Галилеем видимого в его телескоп участка неба есть слабенькая звездочка, которую он не догадался принять за новую неизвестную планету.
Планета Плутон была открыта 21 января 1930 г. Ее орбита вытянута столь сильно, что заходит даже внутрь орбиты Нептуна, как было в течение 20 лет (1979 — 1999).
Смещение перигелия Меркурия, обнаруженное около века назад, не удавалось объяснить по закону Ньютона. Ведь эллиптические орбиты планет не должны меняться со временем, и ближайшая к Солнцу точка орбиты — перигелий — не должна смещаться по отношению к неподвижным звездам. Но перигелий пре-цессировал с малой скоростью, и орбита напоминала поворачивающийся эллипс — не учитываемый эффект — 43" в 100 лет. Само измерение столь малой величины с такой погрешностью — тоже большое достижение (погрешность менее 1 %).
Подозревали, что есть еще одна планета, возмущающая орбиту Меркурия, ее даже условно назвали Вулканом, но не нашли. Появилось мнение, что закон тяготения Ньютона неточен. «Подправил» его в 1915 г. А. Эйнштейн: смещение перигелия планеты Меркурий удалось объяснить только в рамках ОТО (общей теории относительности). Эти поправки играют роль только вблизи больших тяготеющих масс.
По ОТО, перигелии орбит при каждом обороте планеты вокруг Солнца должны перемещаться на долю оборота, равную 3 (v/c)2. Для перигелия Меркурия получается 43", угол поворота перигелия за сто лет составляет 42,91". Эта величина соответствует обработке на-
блюдений за Меркурием с 1765 по 1937 г. Так была объяснена прецессия перигелия орбиты Меркурия. Было показано, что для практических задач закон Ньютона дает хорошие результаты, но для больших скоростей и вблизи больших масс нужны иные законы.
Достижения космонавтики — величайшее подтверждение закона всемирного тяготения. Скорость, с которой должно двигаться тело у поверхности Земли, не падая на нее, называется первой космической. Она определяется из равенства ускорения свободного падения и центростремительного ускорения при условии, что тело движется по круговой орбите с радиусом, равным радиусу Земли, и равна 7,9 км/с. Впервые эта скорость была достигнута 4 октября 1957 г., когда советская ракета вывела на орбиту вокруг Земли первый искусственный спутник массой всего 83,6 кг. Он просуществовал как космическое тело 92 сут, совершив 1400 оборотов вокруг Земли. Искусственные спутники Земли несут трудовую вахту, решая многие задачи (дальняя радиосвязь, телевидение, метеорология, навигация, разведка, сейсмология и др.). Первый спутник был выведен на орбиту советской двухступенчатой ракетой-носителем «Спутник», ставшей основой для семейства ракет «Восток» и «Союз». Принцип действия ракеты можно объяснить с помощью второго и третьего законов Ньютона. Равенство кинетической и потенциальной энергии гравитации служит условием отрыва ракеты от Земли и выхода на параболическую (незамкнутую) траекторию и определяет вторую космическую скорость, равную 11,2 км/с. Старт первой автоматической станции «Луна-1» 2 января 1959 г. позволил впервые преодолеть рубеж второй космической скорости и выйти за пределы околоземного пространства. 12 апреля 1961 г. в космос был выведен космический корабль «Восток» с первым летчиком-космонавтом Ю. А. Гагариным. Так началась новая эра в истории освоения космоса людьми.
У. Гершель, открывший планету Уран и два ее спутника и измеривший звездный параллакс, хотел доказать, что «острова» во Вселенной существуют, каждый из них состоит из миллионов звезд, удерживаемых вместе за счет взаимного притяжения. Как Гюйгенс и Ньютон, он считал, что все звезды имеют одинаковую светимость, и тогда яркая звезда в паре со слабой должна быть ближе, чем слабая, и ее смещение за год будет больше. За 1782—1784 гг. Гершель измерил угловые расстояния почти 700 звезд, но смещения были не те, что он ожидал. Только в 1803 г. он понял, что открыл орбитальные движения звезд, образующих физические пары, компоненты которых движутся вокруг общего центра масс по закону Ньютона (они были названы визуально-двойными). Значит закон тяготения Ньютона всемирен. На его основе Гершель, Кант и Ламберт стали объяснять видимые явления во Вселенной. Гершель открыл двойные звезды, составил каталог двойных и кратных звезд (1784).
Кроме того, Гершель установил, что звезды в некоторых парах имеют разную светимость, а таких пар с отличающимися яркостями в сотни раз оказалось множество. Это не объясняется разной удаленностью звезд в паре. Все наблюдаемые в телескоп звезды образуют вместе с Млечным Путем тот «остров», к которому принадлежит и наше Солнце, а далекие «мировые острова» представляются нам туманностями, как считал и Кант. Гершель решил, что планетарные туманности — звездные системы в последней стадии гравитационного коллапса, а «звезды, их образующие в результате некоторых нарушений или утраты энергии, уже не могут больше поддерживать своего первоначального положения... и, наконец, собираются вместе и вследствие соударений объединяются в новое тело». Это объясняло природу «новой» звезды, которую видел Тихо Браге в 1572 г. в созвездии Кассиопеи, а И. Кеплер в созвездии Змееносца. Гершель обнаружил в 1790 г. новое явление — «звезду примерно 8-й величины со слабосветящейся атмосферой!» Это была планетарная туманность NGC 1514. И он нашел объяснение — это звезда, конденсирующаяся из облака светящегося вещества под действием гравитации. Так У. Гершель еще раз подчеркнул единство Вселенной и роль в этом закона всемирного тяготения.
Итак, подтверждением закона всемирного тяготения являются: в Солнечной системе — предсказание возвращения кометы Галлея, объяснение движений Луны, оценки планетных возмущений, обнаружение планеты Нептун по возмущениям планеты Уран, а затем планеты Плутон, сплюснутость Земли у полюсов, траектории астероидов, полеты космических аппаратов и т. п.; вне Солнечной системы — движение звезд в системе двойных звезд и звездных систем. Но и вне Солнечной системы использование закона тяготения привело к появлению ряда парадоксов (фотометрическому, космологическому и др.), которые были разрешены только в ОТО.
В закон Ньютона входит универсальная гравитационная постоянная G, определенная в опытах Кавендиша. Знание G позволило «взвесить» Землю, определить ее среднюю плотность, которая оказалась больше, чем вблизи поверхности. Значит, плотность растет с глубиной, Земля неоднородна. Это подтверждают и другие исследования, в частности сейсмические. На земной поверхности ускорение свободного падения почти постоянно, отличаясь из-за сплюснутости у полюсов на 0,18 % и из-за центробежных сил при перемещении от экватора к полюсу — на 0,34 %.
Уровень земных морей и океанов, испытывающий периодические изменения, связанные с лунными сутками, зависит от приливного (или дифференциального) гравитационного притяжения. С ним же связаны и другие эффекты. Например, лунные сутки примерно на час длиннее, ось вращения Земли испытывает прецессию с периодом примерно 26 000 лет, большая ось лунной орбиты вращается в прямом направлении (в направлении ее орбитального движения) с периодом почти 9 лет, точки пересе-
чения лунной орбиты с земной (узлы лунной орбиты) движутся несколько назад вдоль орбиты с периодом 18,6 лет и т.д. При этом приливообразующая сила Луны более чем в 2 раза превышает силу Солнца, поскольку эта сила пропорциональна кубу расстояний (что следует из расчета с использованием закона тяготения Ньютона).
Точное и устойчивое решение задачи трех тел, как было показано позднее Лагранжем, возможно только в том случае, когда три тела лежат в вершинах равностороннего треугольника, вращающегося вокруг центра масс данной системы с постоянной угловой скоростью 2π/Т. Эти точки устойчивости определяют оптимальные условия работы космических станций.
