Материальный баланс массообменных процессов

Основы составления материальных балансов, в том числе и массообменных процессов, были рассмотрены в гл. 1. Материальные балансы конкретных массообменных процессов будут даны ниже в соответствующих главах. В этом разделе будет рассмотрен подход к составлению материальных балансов массообменных процессов с учетом их специфики.

Материальные балансы массообменных процессов зависят от способа их проведения. Различают однократное, непрерывное и ступенчатое взаимодействие фаз.

Однократное взаимодействие характерно для периодических процессов, как правило при малой производительное! и. При этом фазы смешиваются, а после завершения процесса разделяются (например, проведение периодического процесса жидкостной экстракции в аппарате с мешалкой).

Материальный баланс такою процесса в целом и по i-му компоненту имеет вид

G_H + L_H = G_K + L_K , (15.7)

G_H · y_iH + L_{H ·} x_{iH =} G_{K ·} y_iK + L_K · x_iK , (15.8)

где С_н и G_к начальное и конечное количество фазы Ф_у; L_н и L_к –начальной и конечное количество фазы Ф_х; у_in и x_in , у_iк и x_iк –начальные и конечные концентрации i-гo компонента в фазах Ф_у и Ф_х соответственно.

Если величины С и L мало изменяются с изменением состава, т. е. G_н ≈ G_к и L_н ≈L_к, то из уравнения (15.8) получаем

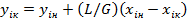. (15.9)

Уравнение (15.9) выражает составы получаемых продуктов раз­деления в зависимости от относительного расхода фаз L/G и является уравнением рабочей линии.

В массообменных аппаратах непрерывного действия процесс может происходить при непрерывном контакте фаз (например, в абсорбционных аппаратах пленочного типа, представляющих собой, по существу, кожухотрубчатый теплообменник, по внут­ренним поверхностям трубок которого течет пленка жидкости, а навстречу этой жидкости движется газ). При этом концентрации распределяемого вещества в фазах изменяются монотонно.

В массообменных аппаратах ступенчатого типа (например, в вертикальных аппаратах с горизонтальными перегородками-тарелками) в каждой ступени происходит взаимодействие фаз (см. разд. 16.53), а по выходе из ступени –их разделение. Проведение процесса при непрерывном и ступенчатом взаимодействии фаз существенно зависит от направления относительного движения фаз (прямоток, противоток и др.) и гидродинамической структуры их потоков.

При непрерывном противотоке, наиболее часто используемом в технике (рис. 15-1, а), материальный баланс для произвольного сечения аппарата при бесконечно малом пути выражается сле­дующими соотношениями:

по всему потоку -dG = dL,

по i-му компоненту -d(Gу_i) = d(Lx_i).

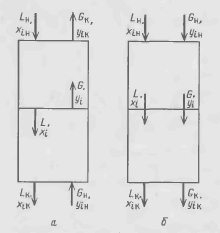
Рис. 15-1. К соединению материального баланса при непрерывном контакте фаз в условиях противотока (а) и прямотока (б)

Интегрирование в пределах от начальных значений входящих в это соотношение величин до их значений в произвольном сечении дает

G_н - L_к = G_к - L_н = G - L

и

G_нy_iн - L_кx_iк = G_кy_iк - L_нx_iн = Gy_i - Lx_i . (15.10)

При малом изменении величин G и L по высоте аппарата

y_i = y_iн + (L/G)(x_i-x_iк) = y_iк + (L/G)(x_i - x_iн). (15.11)

Соотношение (15.11) называют уравнением рабочей линии не­прерывного противоточного массообменного процесса. Оно вы­ражает связь cocтавов взаимодействующих фаз в произвольном сечении аппарата. При L/G = const рабочая линия прямая. Если L/G ¹ const, то рабочая линия отклоняется от прямой.

При непрерывном прямотоке фазы движутся в одном направ­лении (рис. 15-1,6). На рис. 15-1,6 показано движение фаз сверху вниз, но в принципе может осуществляться и противоположное совместное их движение -снизу вверх, при котором между фазами идет процесс массопереноса. Как и в случае противотока, уравнения материального баланса имеют вид (для бесконечно малого пути)

для всего потока -dG = -dL,

для i-го компонента -d (Gу_i) = -d(Lx_i).

Итерирование этих уравнений в пределах изменения пере­менных (от начальных на входе в аппарат до конечных на выходе из него) дает уравнение материальных балансов по потокам и любому i-му компоненту:

G_к - G_н = L_н - L_к, G_нy_iн = L_нx_iн - L_кx_iк

откуда

G_н + L_н = G_к + L_к, G_нy_iн + L_нx_iн = G_кy_iк + L_кx_iк

Для получения более общего уравнения, описывающего изме­нение состава фаз но высоте массообменного аппарата, проин­тегрируем исходные уравнения в пределах от начальных (или конечных) значений величин, входящих в эти уравнения, до их значений в произвольном сечении (см. рис 15-1,6). Тогда получим

G_н + L_н = G + L= const, Gy_i + Lx_i = G_нy_iн + L_нx_iк = const (15.12)

Уравнения (15.12) показывают, что по высоте массообменного аппарата происходит лишь перераспределение i-го компонента между фазами, общее же количество вещества и любого i-го компонента по высоте аппарата остаются неизменными. При усло­вии, что величины G и L мало изменяются по высоте аппарата, из уравнений (15.12) получим выражение

y_i = y_iн-(L/G)(x_i-x_iн), (15.13)

которое является уравнением рабочей линии непрерывного прямоточного массообменного процесса. Сравнение этого уравнения^- с уравнением (15.11) показывает, что они аналогичны по форме, отличаясь лишь знаком перед величиной (L/G)(x_i — x_iн).

Отметим, что уравнения (15,11) и (15.13) получены для условий отсутствия продольного перемешивания в массообменном аппа­рате, т. е. для модели идеального вытеснения.

МОЛЕКУЛЯРНАЯ ДИФФУЗИЯ

Ранее отмечалось (см. гл. 3), что в потоке идут два вида массопереноса—молекулярный и конвективный.

Молекулярная диффузия описывается первым законом Фика:

dM = - DdFdτдc/дn.(15.14)

Для всей поверхности F диффузии первый закон Фика выразится как

М = -DFτдc/дn, (15.14а)

где D - коэффициент молекулярной диффузии; F-поверхность, нормальная к на­правлению диффузии; дс/дп-градиент концентраций вещества на единицу длины пути п диффундирующего вещества; знак минус связан с уменьшением градиента концентраций дс/дп по длине пути диффузии.

Коэффициент молекулярной диффузии D зависит от природы диффундирующего вещества. Поэтому он не связан с динамикой процесса и характеризует способность вещества проникать в какую-либо среду. Найдем его размерность из выражения (15.14a):

,

откуда следует, что коэффициент молекулярной диффузии D пока­зывает, какое количество вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице. Коэффициент молекулярной диффузии D является анало­гом коэффициента температуропроводности а.

Значения D находят по справочникам или рассчитывают. На­пример,

для газов

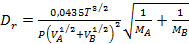, (15.15)

для жидкостей

, (15.16)

где Т -абсолютная температура, К; Р давление, Па; V_A и V_Bмолярные объемы взаимодействующих веществ, см³ /моль; М_А и М_В молярные массы, кг/кмоль; m-вязкость жидкости, в которой происходит диффузия, Па · с.

Таким образом, коэффициент диффузии зависит от температуры (увеличивается с повышением температуры) и для газов -от дав­ления (с увеличением давления D_r снижается).

Для газовой среды D_r ≈ 1 см²/с, для конденсированной (жидкой) среды D_ж ≈ 1 см²/сут, откуда следует, что молекулярная диффузия в жидкостях, а тем более в твердых телах -процесс очень мед­ленный.

Строго говоря, движущей силой процесса молекулярной диф­фузии является градиент химического потенциала вещества (под химическим потенциалом, как известно, понимают частные произ­водные характеристических функций по числам молей компонентов N_i при всех других постоянных параметрах состояния, например дH/дN_i = m_i = дU/дN_i=дG/дN_i ,где Н-энтальпия, V внутренняя энергия, G-энергия Гиббса. Но для случая переноса одного ком­понента m_i=f(с_i), где с_i-концентрация i-го компонента в смеси. Тогда в качестве движущей силы можно использовать градиент концентраций, что намного упрощает расчеты. При невысоких концентрациях компонентов в реальных системах также можно использовать градиент концентраций в качестве движущей силы. Для достаточно концентрированных реальных систем при исполь­зовании в качестве движущей силы градиента концентраций следует учитывать влияние на величину коэффициента молекулярной диффузии состава системы (разделяемой смеси).