Строение ядра. Энергия связи. Радиоактивность

Основные формулы:

Ядро обозначается тем же символом, что и нейтральный атом: 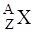, где Z – зарядовое число, определяющее число протонов в ядре, A – массовое число, определяющее число нуклонов (протонов и нейтронов) в ядре.

Закон радиоактивного распада

N=N₀exp(-λt), (4.1)

где N₀ – число ядер в начальный момент времени (t=0), N – число ядер в момент времени t, λ – постоянная радиоактивного распада.

Количество атомов, распавшихся за время t

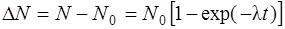(4.2)

Период полураспада T – промежуток времени, за который число ядер уменьшается в два раза. Период полураспада и постоянная распада связаны соотношением

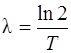(4.3)

Если подставить (4.3) в соотношение (4.1), закон радиоактивного распада можно представить в другом виде

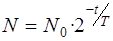(4.4)

В случае, когда промежуток времени Δt мал по сравнению с периодом полураспада Т (Δt<<T), то число распавшихся ядер можно определять по приближенной формуле

ΔN ≈ λ·N·Δt (4.5)

Среднее время жизни τ радиоактивного изотопа – промежуток времени, за который число ядер уменьшается в e раз

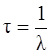(4.6)

Активность радиоактивного изотопа – число ядер, распавшихся в единицу времени

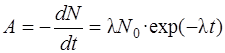(4.7)

начальная активность (при t=0)

A₀=λN₀ (4.8)

Активность изменяется с течением времени по закону

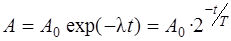(4.9)

Уравнения α- и β- распадов (правила смещения):

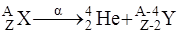(4.10)

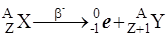(4.11)

Закон поглощения γ-излучения веществом

I=I₀e^–μx, (4.12)

где I₀ – интенсивность γ-излучения, падающая на слой вещества толщиной x, I - интенсивность γ-лучей, прошедших слой x, μ – линейный коэффициент поглощения.

Энергия ядерной реакции (или тепловой эффект реакции)

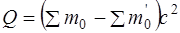, (4.13)

где 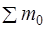и 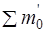- суммы масс покоя частиц, соответственно, до и после реакции, с – скорость света в вакууме. Если 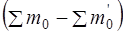>0, то реакция идет с выделением энергии; если 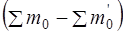<0, то реакция идет с поглощением энергии.

Энергетический выход ядерной реакции чаще измеряют не в системе СИ (Дж), а в МэВ.

В этом случае массу частиц измеряют в атомных единицах массы (а.е.м.), а значение .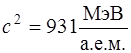

Все ядерные реакции идут в соответствии с законами сохранения заряда, массового числа (число нуклонов), полной энергии и импульса.

Под полной энергией подразумевается полная релятивистская энергия, определяемая по формуле

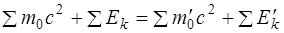, (4.14)

где 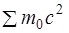- сумма энергий покоя частиц до реакции, 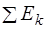- сумма их кинетических энергий. Справа стоят те же физические величины, относящиеся к частицам, образующимся в результате реакции.

Энергия связи ядра, т.е. энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его частицы без сообщения им кинетической энергии, определяется формулой

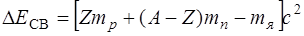(4.15)

где m_p, m_n и m_я , соответственно, массы протона, нейтрона и ядра.

Так как в справочных таблицах приводятся значения масс атомов, а не ядер, надо перейти к соотношению, содержащему эти величины. Масса ядра m_я= m_а-Zm_e, где m_e – масса электрона, тогда

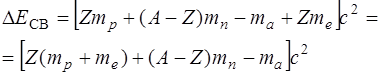
Учитывая, что 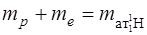- масса атома водорода, можно записать

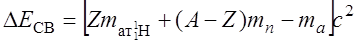(4.16)

Примеры решения задач

Задача 4.1. Вычислить удельную энергию связи ядра магния 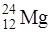. Масса атома магния m_Mg=23,98504 а.е.м.

Решение.

Ядро магния содержит 12 протонов и 12 нейтронов. Согласно формуле (4.16) получим:

.

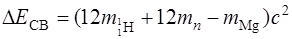Удельная энергия связи ,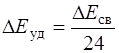

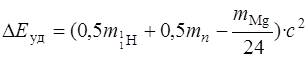
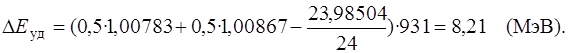
Ответ: ΔЕ_уд=8,21 МэВ.

Задача 4.2. В какой элемент превращается изотоп урана 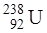после трех α-распадов и двух β^--распадов?

Решение.

Каждый α-распад, согласно правилам смещения (4.10, 4.11), сопровождается уменьшением зарядового числа на 2 и уменьшением массового числа на 4. Каждый β^—распад сопровождается увеличением зарядового числа на единицу без изменения массового числа.

Таким образом, зарядовое число полученного элемента

Z=92-3·2+2·1=88, а массовое число A=238-3·4=226, т.е. получился элемент .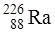

Ответ: .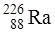

Задача 4.3. Сколько ядер, содержащихся в 1 г трития 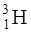, распадается за среднее время жизни этого изотопа?

Решение.

Согласно закону радиоактивного распада (4.1) N=N₀exp(-λt), среднее время жизни радиоактивного изотопа 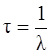, по условию задачи t=τ, следовательно, .

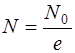Число распавшихся атомов за время t=τ равно

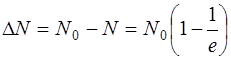
Найдем число атомов N₀, содержащихся в массе m=1 г изотопа :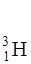

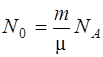
где μ=0,003 кг/моль, N_A– число Авогадро.

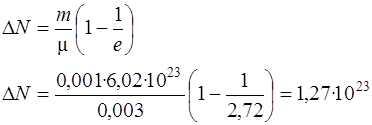
Ответ: ΔN=1,27·10²³.

Задача 4.4. Активность препарата урана–238 равна 2,5·10⁴ Бк, масса препарата равна 2 г. Определить период полураспада урана.

Решение.

Согласно соотношению (4.7) активность радиоактивного препарата равна A=λN. Учитывая, что 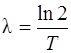, получим

,

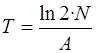где N – число ядер, содержащихся в препарате массой m.

.

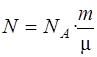Молярная масса μ данного изотопа урана равна 238 г/моль.

Окончательная формула для периода полураспада

.

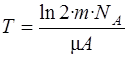
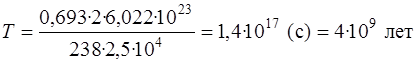Ответ: 4·10⁹ лет.

Задача 4.5. Какую массу воды, взятой при 0 ˚С можно довести до кипения, используя энергию термоядерного синтеза гелия из дейтерия и трития, считая, что на нагревание идет 10% выделяемой энергии. Масса синтезированного гелия 1 г.

Решение.

Уравнение ядерной реакции синтеза

.

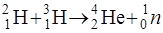Подсчитаем суммарную массу частиц до реакции

Σm_i=2,01410 а.е.м.+3,01605 а.е.м.=5,03015 а.е.м.

Суммарная масса частиц, образовавшихся в результате синтеза

Σm′_i=4,00260 а.е.м.+1,00867 а.е.м.=5,01127 а.е.м.

Результаты расчета показывают, что Σm′_I<Σm_i, следовательно, реакция идет с выделением энергии

Q=(5,03015 - 5,01127)·931=17,6 (МэВ).

Эта энергия выделяется при синтезе одного ядра. В массе образовавшегося гелия содержится ядер

, .

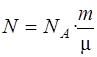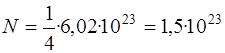Следовательно, полная энергия, выделяемая в данной реакции:

ΔE=Q·N; ΔE=17,6·1,5·10²³=26,5·10²³ (МэВ).

Вода при нагревании получает 10% от ΔE, т.е. 0,1· ΔE=mcΔT, где m – масса воды, c – её удельная теплоемкость, ΔT =100 К.

.

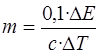Чтобы получить массу воды в кг, перейдем к системе СИ

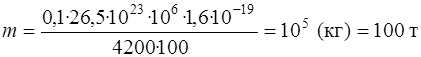
Ответ: m=100 т.

Задача 4.6. Определить кинетические энергии продуктов реакции 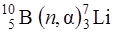, протекающей в результате взаимодействия весьма медленных нейтронов с покоящимися ядрами бора.

Решение.

Ядро бора 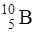, поглотив медленный нейтрон, превращается в ядро 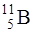, которое, будучи возбужденным, испускает α-частицу (ядро гелия 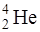), превращаясь в ядро лития 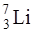. Уравнение реакции имеет вид: .

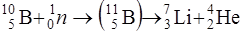Энергию реакции определим по формуле (4.13)

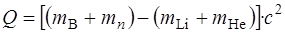
Q = (10,01294+1,00867-7,01601-4,00260)·931=2,8 (МэВ).

Для определения кинетической энергии продуктов реакции применим закон сохранения полной энергии (4.14) с учетом формулы (4.13) .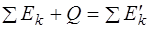

Из условия задачи следует, что величиной ΣЕ_k можно пренебречь (медленный нейтрон, покоящееся ядро бора). Но тогда получим

E_Li+E_He=Q (4.17)

Применим закон сохранения импульса, так как суммарный импульс ядра бора и нейтрона равен нулю, то

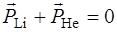или P_Li= P_He.

Учтем, что импульс связан с кинетической энергией по формуле

,

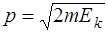получим m_Li E_Li= m_He E_He. (4.18)

Решив систему уравнений (4.17) и (4.18), найдем кинетические энергии продуктов реакции:

.

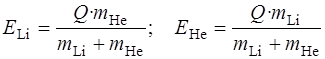Округлив значения масс ядер m_Li и m_He до целых чисел, получим

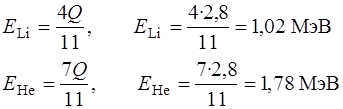
Ответ: E_Li=1,02 МэВ, E_He=1,78 МэВ.

Список литературы

1. Савельев И.В. Курс общей физики. Кн.3. – М.: Наука, 1999.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1998.

3. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1998.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.

5. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл–пресс,1997.

Составители: ХАЙРЕТДИНОВА Адиля Кашафовна,

ШАТОХИН Сергей Алексеевич

СТРОЕНИЕ АТОМА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям

по курсу общей физики

Подписано в печать 11.01.2005 Формат 60 × 84 1/16.

Бумага офсетная. Печать плоская. Гарнитура Times New Roman Cyr.

Усл. печ. л. 2,1. Усл. кр.-отт. 2,1. Уч-изд. л. 2,0.

Тираж 300 экз. Заказ №

Уфимский государственный авиационный технический университет

Центр оперативной полиграфии УГАТУ

450000, Уфа-центр, ул. К. Маркса, 12