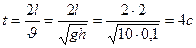Работа. Мощность. Энергия. Закон сохранения энергии

Математический аппарат физики.

Элементы векторной алгебры

1. Физические величины могут быть скалярными или векторными. Скалярными величинами (скалярами) называются такие, которые характеризуются только числовым значением. Примерами скалярных величин являются время, масса, температура, электрический заряд, потенциал и др. Скалярные величины могут быть положительными и отрицательными и складываются алгебраически.

Пример 1.

Определить полный заряд системы, если q₁= 2 нКл, q₂= -7нКл, q₃= 3 нКл.

Решение.

Полный заряд системы q=q₁₊ q₂₊ q₃= (2 - 7 + 3) ∙ 10^-9Кл= - 2 нКл.

Векторными величинами (векторами) называются такие, которые характеризуются числовым значением и направлением. Примерами векторных величин являются скорость, ускорение. Сила. Импульс, напряженность электрического поля. Магнитная индукция и др. Векторные величины складываются геометрически.

Пример 2.

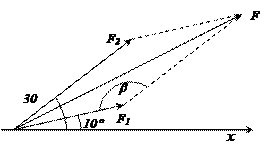Найти равнодействующую двух сил F₁=3Н и F₂= 4Н, если векторы F₁ и F₂ составляют с осью x углы 10° и 40° соответственно.

Решение.

Вектор направлен по диагонали параллелограмма, построенного на векторах 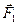и 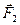. Модуль вектора находим по теореме косинусов:

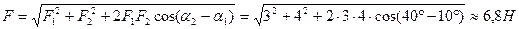
2. Скалярным произведением векторов 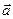и 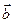называется скаляр, равный произведению числовых значений векторов 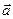и 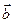, умноженному на косинус угла между ними:

с=a∙b∙cos α

Пример 3.

Найти работу постоянной силы F=20Н, если перемещение тела 7,5 м. а угол между силой и перемещением 120°.

Решение.

Работа силы, по определению, равна скалярному произведению силы и перемещения:

А=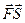

A=F∙S∙cos α=20 ∙7,5∙cos120°= -75 Дж

3. Векторным произведением векторов 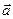и 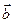называется вектор 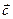, численно равный произведению числовых значений векторов 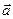и 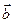, умноженному на синус угла между ними:

c=a∙b∙sin α

Вектор 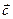перпендикулярен плоскости, в которой лежат векторы 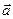и 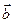, причем его направление связано с направлением векторов 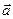и 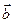правилом буравчика.

Элементы дифференциального и интегрального исчислений

1. Пусть в некоторой области значений x существует функция f(x). Обозначим

∆x=x₁-x₂, f(x)=f(x₁)-f(x₂). Выражение

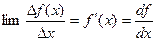
называется первой производной функции f(x) по аргументу x. Графически 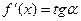, где α – угол наклона касательной к кривой в точке А к оси абсцисс.

Производные некоторых функций

функция	производная	функция	производная
c=const xn ax ex ln x	0 n∙xn-1 ax∙ln a ex 1/x	sin x cos x tg x ctg x	cos x -sin x 1/cos2x -1/sin2x

4. Пусть в некоторой области значений x существует функция f(x). Разобьем интервал ab изменения x на отрезки ∆x₁, ∆x₂, ∆x₃ .. .∆x_n. Составим сумму 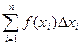. Выражение

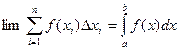
называется определенным интегралом.

Неопределенные интегралы некоторых функций

функция	интеграл	функция	интеграл
xn		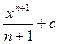sin x	-cos x+с
ex	ex	cos x	sin x+с
1/x	ln|x|+c	tg x	-ln|cosx|+c
		ctg x	ln|sinx|+c

Кинематика

1. Средняя путевая скорость определяется как отношение пути, пройденного телом, ко времени движения:

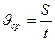
1. Поступательное движение материальн6ой точки ( или твердого тела) характеризуются линейной скоростью:

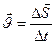
Вектор скорости неравномерного движении можно также найти как первую производную от вектора перемещения по времени

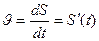
Если движение переменное, то его характеризуют ускорением

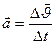
где 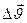- изменение вектора скорости за время 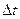. Для прямолинейного равнопеременного движения ускорение остается постоянным по величине и направлению. Вектор ускорения переменного движения можно найти как первую производную от вектора скорости по времени

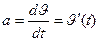
Уравнение пути и скорости имеют вид:

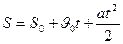
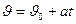
где 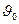- начальная скорость тела.

1. Тело может одновременно участвовать в двух и более движениях. Так, тело брошенное горизонтально со скоростью 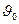с некоторой высоты h, участвует в двух независимых движениях: равномерном и прямолинейном движении по горизонтали и свободном падении по вертикали. В координатах xy эти уравнения запишутся

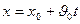
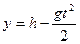
Скорость в любой точке криволинейной траектории определяется:

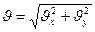
где ,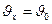

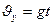
Аналогично рассматривается движение тела, брошенного под углом к горизонту.

1. При движении тела по окружности скорость направлена по касательной к окружности, а центростремительное ускорение по радиусу к центру

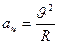
Полное ускорение: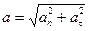

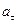и 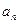- тангенциальное и нормальное ускорения;

Для равномерного вращательного движения угловая скорость равна

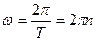
где T – период вращения, n –частота обращения (число оборотов в единицу времени). Уравнение движения при равномерном вращении .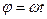

Линейная скорость и ускорение связаны с угловой скоростью соотношениями:

,

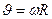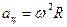
При вращении с ускорением полное ускорение:

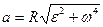
w - угловая скорость; e - угловое ускорение; R - радиус окружности.

При равнопеременном вращении тела уравнение зависимости угловой скорости от времени имеет вид:

,

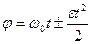а формула зависимости угловой скорости от времени:

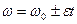
В этих формулах выбирают знак «+» для равноускоренного вращения, знак «-» для равнозамедленного. Также, угловая скорость может быть выражена как первая производная от угла поворота по времени

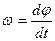
Угловое ускорение при равнопеременном вращении можно найти как первую производную от угловой скорости по времени

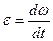
1. Во всех задачах раздела «Кинематика» сопротивление воздуха не учитывается. Если это особо не оговорено в условии задачи.

Пример 4.

Точка движется вдоль оси x согласно уравнению 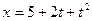, где t – время в секундах. Найти среднюю скорость движения за первые 5 с.

Решение.

Средняя скорость движения тела за время от 0 с до 5 с по определению равна

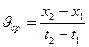
- координата тела в момент времени =0 с,

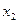- координата тела в момент времени 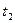=5 с.

Отсюда

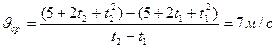
Пример 5.

Уравнения движения тела дано в виде x=15t+0,4t². Определить скорость тела через 5 с и ускорение тела.

Решение.

По определению скорости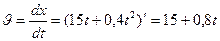

Тогда 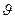=(15+0,8∙5)=19 м/с

Ускорение =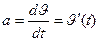

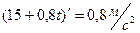
Пример 6.

С какой высоты падало тело, если последние 3 м пути оно пролетело за 0,2 с?

Решение.

Тело падает с высоты 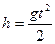, где t- полное время падения. В момент 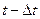оно находилось на высоте 3 м от поверхности. Поэтому можно написать

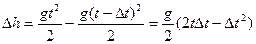
Отсюда находим время падения тела

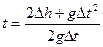, t=1,6 с

Следовательно, тело падало с высоты 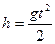=12,8 м

Пример 7.

Максимальная скорость камня, брошенного под углом к горизонту, в 2 раза больше минимальной. Определить под каким углом к горизонту был брошен камень.

Решение.

В направлении оси x камень движется равномерно, поэтому в любой точке траектории 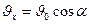. В направлении оси y движение камня равнопеременное. Скорость камня максимальна в точках бросания и падения, а минимальна в верхней точке траектории. Из приведенных рассуждений следует, что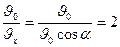

cos α=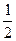

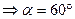
Пример 8.

Найти угловую скорость равномерно вращающегося диска, если линейная скорость точек на ободе 5 м/с, а точки, расположенные на 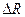=20 см ближе к оси вращения,

Имеют скорость 3м/с.

Решение.

Угловая и линейные скорости точек вращающегося диска связаны соотношением

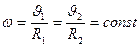, так как вращение равномерное.

Следовательно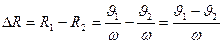

Отсюда находим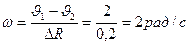

Динамика

1. Основным законом динамики поступательного движения является второй закон Ньютона:

,

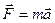где 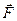- равнодействующая всех сил, приложенных к телу массой m, 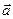- ускорение тела.

При решении задач по динамике необходимо обратить особое внимание на правильное использование второго закона Ньютона. Сначала нужно сделать рисунок, на котором указываются все силы, действующие на тело, и выбирается система отсчета. Затем записывается второй закон Ньютона в векторной форме:

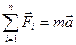
где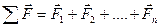

Наконец, данное векторное уравнение нужно спроецировать на выбранные направления осей x и y и решить полученную систему уравнений. Если в движении находится не одно, а несколько связанных между собой тел, то необходимо для каждого тела в отдельности выполнить все вышеуказанные действия и решить полученную систему уравнений.

2. В механике приходится иметь дело со следующими силами:

1) силой тяжести ;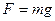

2) силой трения 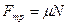, где 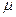- коэффициент трения, N- сила нормальной реакции опоры;

3) силой упругости 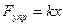, где k- коэффициент жесткости, x- величина деформации тела.

3. Закон Всемирного тяготения, для любых тел массами m₁ и m₂, находящихся на расстоянии r:

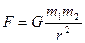
где G=6,67∙10^-11Н∙м²/кг²- гравитационная постоянная

4. В замкнутой системе справедлив закон сохранения импульса

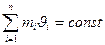
где m_i- масса отдельно взятого тела в системе взаимодействующих тел, 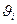- скорость этого тела, n- число взаимодействующих тел. Для двух тел, закон сохранения импульса примет вид:

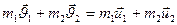
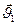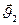где и - скорости тел до их взаимодействия, 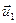и 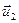- скорости тел после взаимодействия. При решении задач записываем закон сохранения импульса в векторной форме, выбираем направление осей координат и проецируем на них обе части векторного уравнения.

5. Основное уравнение динамики вращательного движения относительно неподвижной оси:

М = Je

где М – результирующий момент внешних сил, действующих на тело;

e - угловое ускорение;

J - момент инерции тела относительно оси вращения.

Моменты инерции некоторых тел массы m

Твердое тело	Момент инерции
обруч радиусом R - относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)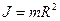
диск радиусом R - относительно оси, перпендикулярной плоскости диска, сплошной цилиндр относительно оси вращения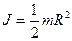
стержень длины l - относительно оси, перпендикулярной стержню и проходящей через его середину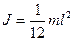
стержень длины l - относительно оси, перпендикулярной стержню и проходящей через его конец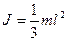
шар радиусом R - относительно оси, проходящей через его центр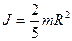

6. Момент импульса тела, вращающегося относительно неподвижной оси:

L = Jw,

где w – угловая скорость тела.

Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:

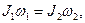
где J₁ и w₁ – момент инерции системы тел и угловая скорость вращения в начальный момент времени; J₂ и w₂ – момент инерции и угловая скорость в конечный момент времени.

Пример 9.

Брусок массой m₂=3 кг движется по поверхности стола под действием силы натяжения нити. Нить перекинута через блок, укрепленный в конце стола. На другом конце нити висит брусок массой m₁=2 кг, падающий вниз. Найти ускорение, с которым движутся бруски. Коэффициент трения 0,2.

Решение.

По второму закону Ньютона для обоих брусков можно написать:

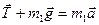
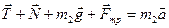
В проекциях на оси x и y:

m₁ 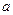=m₁g - T

m₂a=T - F_тр,

Учитывая, что F_тр=μmg и складывая эти уравнения, получим:

a(m₁+m)=g(m₁-μm₂)

Тогда

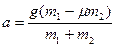= 2,8 м/с²

Пример 10.

Чему равно ускорение свободного падения на высоте, равной радиусу Земли?

Решение.

На поверхности Земли сила тяжести равна силе Всемирного тяготения:

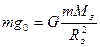
где m- масса тела, M_з- масса Земли, R_з – радиус Земли. На высоте h от поверхности Земли сила тяжести будет равна:

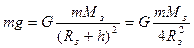
Тогда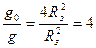

Отсюда находим g=2,5м/с²

Пример 11.

Шарик массой 500 г, подвешенный на нерастяжимой нити длиной 1 м, совершает колебания в вертикальной плоскости. Найти силу натяжения нити в момент, когда она образует с вертикалью угол 60°. Скорость шарика в этот момент 1,5 м/с.

Решение.

На шарик действуют сила тяжести и сила натяжения нити. Запишем для шарика второй закон Ньютона:

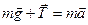
Направляя ось y вдоль радиуса, и проецируя на нее уравнение, получаем:

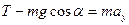
При движении по окружности ускорение центростремительное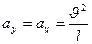

Тогда

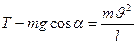
Выразим силу натяжения:

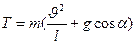
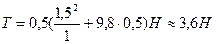
Пример 12.

Средняя высота спутника над поверхностью Земли 1700 км. Определить его скорость и период вращения.

Решение.

Движение по круговой орбите происходит под действием только силы тяготения со стороны Земли:

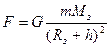
где R_з- радиус Земли, M_з- масса Земли. По второму закону Ньютона: 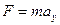, где 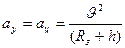- центростремительное ускорение. Тогда

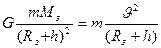
Откуда

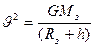
Умножая числитель и знаменатель уравнения на R_з², получаем:

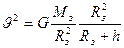
Так как 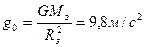, следовательно 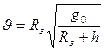=7,01∙10³м/с

Период вращения спутника по круговой орбите радиусом R_З+h:

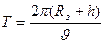=7,24 ∙ 10³с

Пример 13.

Снаряд, летящий со скоростью 100м/с. Разорвался на два осколка. Большой осколок, масса которого равна 0,8 массы снаряда, продолжал двигаться со скоростью 200 м/с в прежнем направлении. Найти величину скорости меньшего осколка.

Решение.

По закону сохранения импульса можно записать

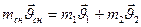
По условию движение снаряда и осколков происходит по одной прямой, поэтому

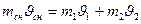
Так как масса большего осколка m₁=0,8m_сн, а меньшего m₂=0,2m_сн, тогда скорость меньшего будет:

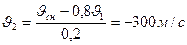
Знак «-» указывает, что меньший осколок полетит в противоположную сторону. Требуется определить величину скорости, т.е.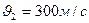

Работа. Мощность. Энергия. Закон сохранения энергии.

1. Работой постоянной силы называется величина

,

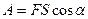где F- сила, действующая на тело, S- перемещение под действием силы, α- угол между направлениями силы и перемещения. Если на тело действует переменная сила, то работу переменной силы надо рассчитывать по формуле

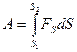
где F_S=Fcosα- проекция силы на перемещение.

1. Мощность определяется работой в единицу времени

N=

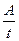
1. Движущееся тело обладает кинетической энергией

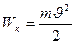
Тело, поднятое над Землей на высоту h, обладает потенциальной энергией

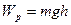
Сжатая или растянутая пружина обладает потенциальной энергией

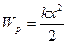
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:

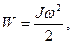или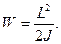

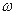- угловая скорость тела;

J - момент инерции тела относительно оси вращения.

4. Под полной механической энергией тела понимают сумму кинетической и потенциальной энергий

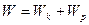
Для замкнутой системы тел, если между телами системы действуют только консервативные силы, т.е. при отсутствии сил трения или сопротивления, полная механическая энергия остается постоянной

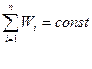
1. Когда на тело или систему тел действуют внешние силы. Полная механическая энергия тела изменяется. При этом справедливо соотношение

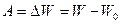
где А – работа внешних сил. Это же соотношение справедливо, когда в замкнутой системе тел между ними действуют неконсервативные силы, например, силы трения. В этом случае А – работа неконсервативных сил.

Пример 14.

Пуля, летящая со скоростью 400 м/с. Попадает в вал и проходит до остановки путь 0,5 м. Определить силу сопротивления вала движению пули. Если ее масса 24 г.

Решение.

По определению работы:

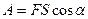
Проведем ось x в направлении движения пули. Тогда угол между направлениями силы и перемещения .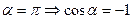

То есть

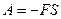
С другой стороны

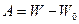
По условию 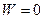, а

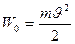
Приравнивая выражения работы, получаем: 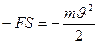, откуда

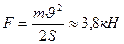
Пример 15.

Груз массой 5 кг свободно падает с некоторой высоты и достигает поверхности земли за 2,5 с. Найти работу силы тяжести.

Решение.

Полная работа силы тяжести

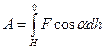
Преобразуем выражение, с учетом того, что угол между направлениями силы и перемещения .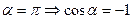

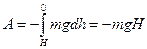
Так как 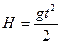, то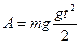

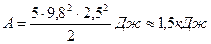
Пример 16.

С горы высотой 6 м и длиной 10 м скользит тело массой 2 кг. Найти его кинетическую энергию у основания горы. Коэффициент трения 0,5.

Решение.

При соскальзывании тела часть механической энергии тратится на работу силы трения. Тогда по закону сохранения энергии

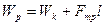
Сила трения 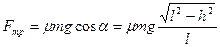, так как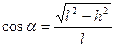

Поэтому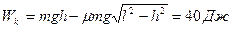

Пример 17.

Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длиной 2 м и высотой 10 см.

Решение.

По закону сохранения энергии:

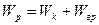
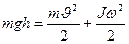
Момент инерции обруча:

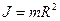
Линейная скорость связана с угловой скоростью соотношением:

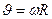
Тогда получим:

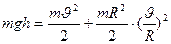
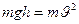
Отсюда скорость обруча у основания наклонной плоскости: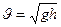

Путь при равноускоренном движении: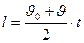

С учетом того, что начальная скорость равна нулю, выразим время: