Спектральные серии излучения атомарного водорода
 Как показывает опыт, в отличие от непрерывного спектра рассматриваемого в курсе оптики, излучение невзаимодействующих друг с другом атомов состоит из отдельных спектральных линий. В соответствии с этим спектр испускания атомов называется линейчатым. Изучение атомных спектров послужило ключом к познанию строения атомов. Оказалось, что каждому газу присущ вполне определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко стоящих линий - серий линий. Отчетливее всего это наблюдается в спектре водорода, простейшего атома. На спектре водорода, рис.13, обозначены видимые линии: Ha; Hb; Hg; Hd; …; H
Как показывает опыт, в отличие от непрерывного спектра рассматриваемого в курсе оптики, излучение невзаимодействующих друг с другом атомов состоит из отдельных спектральных линий. В соответствии с этим спектр испускания атомов называется линейчатым. Изучение атомных спектров послужило ключом к познанию строения атомов. Оказалось, что каждому газу присущ вполне определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко стоящих линий - серий линий. Отчетливее всего это наблюдается в спектре водорода, простейшего атома. На спектре водорода, рис.13, обозначены видимые линии: Ha; Hb; Hg; Hd; …; H 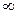 - конец серии. Расстояние между линиями убывает по мере перехода к более коротким длинам волн Швейцарский физик БАЛЬМЕР (1885 г.) обнаружил, что длины волн этой серии водорода могут быть достаточно точно представлены эмпирической формулой:
- конец серии. Расстояние между линиями убывает по мере перехода к более коротким длинам волн Швейцарский физик БАЛЬМЕР (1885 г.) обнаружил, что длины волн этой серии водорода могут быть достаточно точно представлены эмпирической формулой:
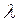 =
= 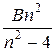 (2.1)
(2.1)
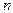 = 3,4,5,6 и
= 3,4,5,6 и 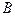 - эмпирическая константа. Формулу (2.1) можно преобразовать с учетом:
- эмпирическая константа. Формулу (2.1) можно преобразовать с учетом: 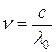 сек -1 , где с - скорость света в вакууме, l0 - длина волны света в
сек -1 , где с - скорость света в вакууме, l0 - длина волны света в
вакууме. Следовательно:
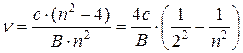
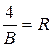 - постоянная Ридберга. R = 1,097×10-7 м-1, и окончательно:
- постоянная Ридберга. R = 1,097×10-7 м-1, и окончательно:
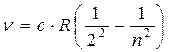 (2.2)
(2.2)
Это формула Бальмера, из которой видно, что с ростом n разность между частотами уменьшается и при n = 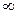 n =
n = 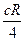 . Предельная частота, около которой сгущаются линии при n ®
. Предельная частота, около которой сгущаются линии при n ®  ¥ называется границей серии. Наряду с серией Бальмера в спектре атомарного водорода обнаружен ряд других серий (начало XX века). В ультрафиолетовой области находится серия Лаймана:
¥ называется границей серии. Наряду с серией Бальмера в спектре атомарного водорода обнаружен ряд других серий (начало XX века). В ультрафиолетовой области находится серия Лаймана:
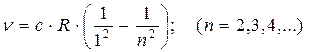
В инфракрасной области спектра были обнаружены:
серия Пашена - 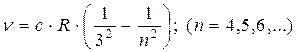
серияБреккета - 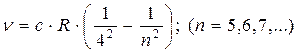
серияПфунда - 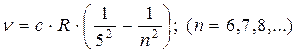
серияХэмфри - 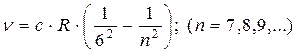
Все эти серии можно представить обобщенной формулой Бальмера:
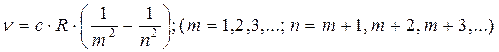 (2.2)
(2.2)
Сравнивая формулы для каждой из серий, можно увидеть, что постоянный член каждой из этих формул является одним из переменных членов в другой. То есть: Частоту любой спектральной линии водородного спектра можно представить как разность двух членов типа R/m2 при каких-нибудь целых значениях m. Это - комбинационный принцип - принцип РИТЦА. Если обозначить 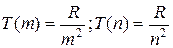 , то можно записать:
, то можно записать: 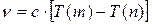 . Числа
. Числа 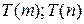 носят название - спектральные (или энергетические) термы. Для атома водорода вся система термов получается из общей формулы:
носят название - спектральные (или энергетические) термы. Для атома водорода вся система термов получается из общей формулы:
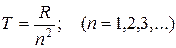
Тогда комбинационный принцип можно сформулировать следующим образом: Если известны частоты двух спектральных линий одной и той же серии, то их разность будет также частотой некоторой третьей спектральной линии, принадлежащей тому же атому. Пусть даны частоты двух линий серии Лаймана:
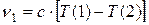 и
и 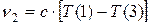 ,
,
тогда 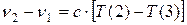 - частота первой линии серии Бальмера.
- частота первой линии серии Бальмера.
Необходимо отметить, что формула Бальмера получена из экспериментальных данных и теории чисел. При этом не использовались какие либо физические принципы.
